Efficiently convert fractions to percentages using our Fraction to Percent Calculator on examples.com. Obtain accurate, quick results with our user-friendly interface.

How to Use Fraction To Percent Calculator

Step 1: Enter the Numerator

Type the numerator of the fraction into the first input box. From the image, the provided numerator is “1.”

Step 2: Enter the Denominator

Type the denominator of the fraction into the second input box. From the image, the provided denominator is “2.”

Step 3: Click Calculate

Press the “Calculate” button to convert the fraction to a percentage.

Step 4: View the Result

The result will be displayed below the calculate button. For the input values from the image (1/2), the result shown is “The percentage is 50%.”

These steps correspond to the calculator setup as depicted in your provided image, demonstrating how to convert the fraction 1/2 into a percentage.

Fraction To Percent Calculator Formula

To convert a fraction to a percentage, the calculation is direct and easy to follow. Here’s the detailed formula and step-by-step process:

Formula:
Percentage=(Numerator/Denominator)×100

Numerator: This is the top number of the fraction, representing the part of the whole.
Denominator: This is the bottom number of the fraction, representing the total or whole.

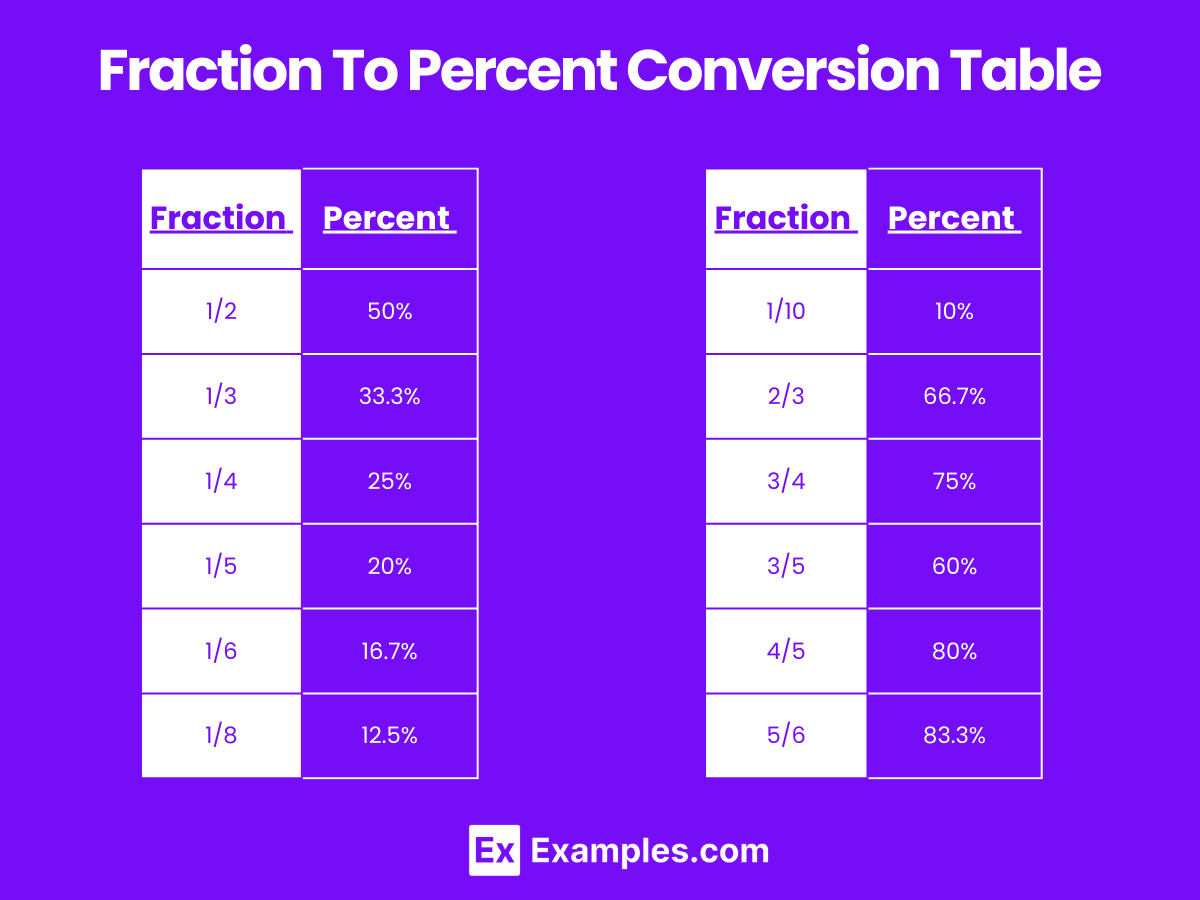
Fraction To Percent Conversion Table

Fraction	Percentage
1/2	50%
1/3	33.3%
1/4	25%
1/5	20%
1/6	16.7%
1/8	12.5%
1/10	10%
2/3	66.7%
3/4	75%
3/5	60%
4/5	80%
5/6	83.3%
7/8	87.5%
1/7	14.3%
2/5	40%
2/7	28.6%
3/8	37.5%
4/9	44.4%
5/7	71.4%
6/7	85.7%

Fraction To Percent Conversion Chart

Examples of Fraction To Percent Calculator

Convert 3/5 to a percentage:
- Numerator: 3
- Denominator: 5
- Calculation: 3/5=0.6→0.6×100=60%
- Result: 3/5 is 60%.
Convert 2/3 to a percentage:
- Numerator: 2
- Denominator: 3
- Calculation: 2/3=0.6667→0.6667×100=66.67%
- Result: 2/3 is approximately 66.67%.
Convert 1/8 to a percentage:
- Numerator: 1
- Denominator: 8
- Calculation: 1/8=0.125→0.125×100=12.5%
- Result: 1/8 is 12.5%.
Convert 4/7 to a percentage:
- Numerator: 4
- Denominator: 7
- Calculation: 4/7=0.5714→0.5714×100≈57.14%
- Result: 4/7 is approximately 57.14%.
Convert 7/9 to a percentage:
- Numerator: 7
- Denominator: 9
- Calculation: 7/9=0.7778→0.7778×100=77.78%
- Result: 7/9 is approximately 77.78%.

How do I handle fractions with large numerators and denominators?

For large fractions, simplifying them first can make calculations easier. Otherwise, follow the standard steps for conversion.

How do I convert repeating decimals to percentages if they come from a fraction?

For repeating decimals derived from a fraction, convert the repeating decimal into a fraction (using algebra, if needed). Once you have the fraction, convert it to a percentage as usual.

What if the denominator is zero in my fraction when converting to a percentage?

A fraction with a denominator of zero is undefined and cannot be converted to a percentage.

How does converting fractions to percentages help with data representation?

Percentages are often more easily understood in data visualization and comparison compared to fractions.

Can percentages greater than 100% be meaningful when derived from fractions?

Yes, percentages over 100% are meaningful, especially when the fraction is greater than one, representing more than a whole.

Why is it important to understand fractions and percentages together?

Understanding both is crucial for mathematical literacy, helping with data analysis, financial literacy, and problem-solving.

Are there any common errors when converting fractions to percentages?

Common errors include not multiplying by 100 after dividing, misinterpreting mixed numbers, and confusing repeating decimals during conversion. Double-checking calculations can prevent these errors.

How does converting fractions to percentages help in academics?

In academics, this conversion is essential for grading, data interpretation, and understanding proportions in various subjects like math and science.