Factors

Factors are the building blocks of numbers, representing integers that evenly divide into another number without leaving a remainder. Understanding factors is crucial for mastering basic arithmetic, simplifying fractions, and exploring more complex mathematical concepts such as greatest common divisors and prime factorization. This guide, enriched with practical examples, demystifies the concept of factors, making it accessible and engaging for learners seeking to deepen their mathematical knowledge.

What are the Factors? 

Factors are numbers that we can multiply together to get another number. Simply put, when two numbers are multiplied and the result is a certain number, those two numbers are called factors of the resulting number. For example, if we multiply 2 and 3 to get 6, then 2 and 3 are factors of 6. Factors are like building blocks of numbers, showing us which numbers can be combined to create a new number through multiplication.

What is the Best Example of Factors?

A classic example to illustrate factors is the number 12. To find its factors, we look for all the pairs of numbers that, when multiplied together, equal 12. These pairs are:

• 1 and 12 (because 1 × 12 = 12)
• 2 and 6 (because 2 × 6 = 12)
• 3 and 4 (because 3 × 4 = 12)

So, the factors of 12 are 1, 2, 3, 4, 6, and 12. This example clearly demonstrates how factors work: they are numbers that divide into another number without leaving a remainder, fitting together like pieces of a puzzle to form the original number. Understanding factors helps in many areas of math, including simplifying fractions and finding the greatest common divisor.

Properties of Factors

When teaching the concept of factors in mathematics, it’s essential to highlight their fundamental properties. Understanding these properties not only aids students in grasping the concept but also empowers teachers to devise more effective teaching strategies. Here’s a guide to the key properties of factors:

• Divisibility: A factor of a number perfectly divides that number without leaving a remainder. For instance, 4 is a factor of 20 because 20 divided by 4 equals 5, with no remainder.
• Uniqueness: Each number has a unique set of factors. This property can be a great starting point for exercises in identifying factors, encouraging students to explore numbers and their factors.
• Inclusivity of 1 and Itself: Every number has at least two factors: 1 and the number itself. This is a fundamental aspect that can be used to introduce the concept of factors to beginners.
• Pairing: Factors of a number come in pairs that multiply to the number. This can be a fun and interactive way to teach factors, using multiplication tables or factor trees.
• Prime and Composite: Understanding that prime numbers have only two factors, 1 and themselves, while composite numbers have more than two, is crucial. This distinction helps students in factorization and simplifying fractions.

How to Find Factors of a Number?

Finding factors of a number is a fundamental concept in mathematics that is crucial for various topics such as division, multiplication, fractions, and algebra. Understanding how to determine the factors of a number helps students develop critical thinking and problem-solving skills. Here is a detailed guide on how to find factors, optimized for clarity and comprehension:

Understanding Factors

Factors are numbers you can multiply together to get another number. For example, 2 and 3 are factors of 6, because 2 × 3 = 6. A number can have multiple pairs of factors, and 1 and the number itself are always its factors.

1. Division Method

The division method is a straightforward approach to finding all factors of a number. This method involves dividing the number by integers starting from 1 and moving up to the number itself.

• Step 1: Start with the number 1. Since 1 multiplied by any number gives that number, 1 is always a factor.
• Step 2: Move to the next integer and divide the number by this integer.
• Step 3: If the division results in a whole number (no remainder), then both the divisor and the quotient are factors of the number.
• Step 4: Continue this process with successive integers until you reach the original number.

Finding Factors of 24 By Using Division Method

Division	Result	Conclusion
24 ÷ 1	24	1 and 24 are factors of 24
24 ÷ 2	12	2 and 12 are factors of 24
24 ÷ 3	8	3 and 8 are factors of 24
24 ÷ 4	6	4 and 6 are factors of 24
24 ÷ 5	–	5 is not a factor of 24
24 ÷ 6	4	Already listed

From these calculations, we identify the factors of 24 as 1, 2, 3, 4, 6, 8, 12, and 24.

Step 1: Begin with the smallest factor, which is always 1. Dividing 24 by 1 (24÷1) gives 24, confirming that 1 and 24 are factors.

Step 2: Move to the next integer, 2, and divide 24 by 2 (24÷2). The quotient is 12, which means 2 and 12 are factors.

Step 3: Continue to 3, dividing 24 by 3 (24÷3). The quotient is 8, identifying 3 and 8 as factors.

Step 4: Proceed to 4, and divide 24 by 4 (24÷4). The quotient is 6, so 4 and 6 are factors.

Step 5: Test the next integer, 5, by dividing 24 by 5 (24÷5). Since it does not result in a whole number, 5 is not a factor.

Step 6: Continue this process with successive integers up to 12. Since dividing 24 by 12 (24÷12) results in 2, and both 12 and 2 have already been identified as factors, all factors of 24 have been found.

2. Multiplication Method

Another approach is to use multiplication, focusing on finding factor pairs that multiply to the number.

• Step 1: Start with the number 1 and the number itself as the first factor pair.
• Step 2: Increment the first number of the pair and find a corresponding number that multiplies to the original number.
• Step 3: Continue finding new pairs until you reach a pair where the numbers are repeated or when the first number exceeds the square root of the original number.

 Finding Factors of 24 By Multiplication Method

Multiplication	Result	Conclusion
1 × 24	24	1 and 24 are factors of 24
2 × 12	24	2 and 12 are factors of 24
3 × 8	24	3 and 8 are factors of 24
4 × 6	24	4 and 6 are factors of 24

From these calculations, we identify the factors of 24 as 1, 2, 3, 4, 6, 12, and 24.

Step 1: Start with the number 1. Multiplying 1 by 24 (1×24) gives 24, confirming that 1 and 24 are factors.

Step 2: Move to the next integer, 2. Multiply 2 by 12 (2×12), which equals 24, indicating that 2 and 12 are factors.

Step 3: Continue to 3. Multiply 3 by 8 (3×8), resulting in 24, so 3 and 8 are factors.

Step 4: Proceed to 4. Multiply 4 by 6 (4×6), which equals 24, confirming that 4 and 6 are factors.

Step 5: Check if further multiplication is necessary. After 4×6, any further multiplication would only repeat the factor pairs we’ve already found, so we conclude the process here.

By following these steps, we systematically determine all the factors of 24 using the multiplication method, ensuring a comprehensive understanding of the factorization process.

Factor Pairs

Factor pairs are a fundamental concept in mathematics, especially when it comes to understanding the factors of a number. A factor pair consists of two numbers that, when multiplied together, equal the original number. This concept is crucial for various mathematical operations and problem-solving scenarios.

Understanding Factor Pairs

Factor pairs simplify the process of finding all factors of a number by focusing on the multiplication aspect rather than division. Each pair contributes to a deeper understanding of the number’s properties and its relationships with other numbers.

How to Identify Factor Pairs

To identify factor pairs of a number:

1. Start with One: Begin with the number 1 and the original number itself as the first factor pair since 1 multiplied by any number gives that number.
2. Incrementally Find Pairs: Increase the first number in the pair and find a corresponding second number that, when multiplied, equals the original number.
3. Use Systematic Approach: Continue this process, moving systematically through integers, until reaching a point where the first number in the pair is greater than the square root of the original number, indicating all factor pairs have been found.

 Factor Pairs of 36

Factor Pair	Multiplication	Result
1 and 36	1 × 36	36
2 and 18	2 × 18	36
3 and 12	3 × 12	36
4 and 9	4 × 9	36
6 and 6	6 × 6	36

The factor pairs of 36 are (1, 36), (2, 18), (3, 12), (4, 9), and (6, 6), which also gives us the complete set of factors: 1, 2, 3, 4, 6, 9, 12, 18, and 36.

List of Factors

Product	Factors
6	1, 2, 3, 6
12	1, 2, 3, 4, 6, 12
15	1, 3, 5, 15
18	1, 2, 3, 6, 9, 18
24	1, 2, 3, 4, 6, 8, 12, 24
36	1, 2, 3, 4, 6, 9, 12, 18, 36
48	1, 2, 3, 4, 6, 8, 12, 16, 24, 48
60	1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60

Factors of Perfect Numbers

Perfect numbers hold a special place in the realm of mathematics due to their unique and intriguing properties. A perfect number is defined as a positive integer that is equal to the sum of its proper divisors, excluding the number itself. Understanding the factors of perfect numbers offers insight into their symmetrical and harmonious nature.

Understanding Perfect Numbers

To fully grasp what makes a number perfect, one must first understand its factors. The factors of a number include all the integers that divide into it evenly, excluding the number itself when considering perfect numbers. The sum of these factors, when equal to the original number, categorizes it as perfect.

Identifying Factors of Perfect Numbers

Finding the factors of perfect numbers involves the same process as finding factors for any integer. However, the unique aspect is that when these factors are summed, they equal the number itself. This characteristic is what defines a perfect number.

Examples of Perfect Numbers

• 6: The factors of 6 are 1, 2, and 3. The sum $1+2+3=6$, making 6 a perfect number.
• 28: The factors of 28 (excluding 28) are 1, 2, 4, 7, and 14. The sum 1+2+4+7+14=28, thus 28 is a perfect number.

Different Types of Factors

In mathematics, factors play a crucial role in various calculations and problem-solving scenarios. Understanding the different types of factors is essential for students, educators, and anyone interested in the field of mathematics. This comprehensive guide will explore the various types of factors, including prime factors, composite factors, proper factors, and more, providing insights into their definitions, characteristics, and applications.

1. Prime Factors

Prime factors are the building blocks of numbers. A prime factor is a factor that is a prime number, which means it can only be divided by 1 and itself without leaving a remainder. The process of breaking down a number into its prime factors is known as prime factorization.

• Characteristics: Prime numbers are greater than 1 and have exactly two distinct positive divisors: 1 and the number itself.
• Example: The prime factors of 30 are 2, 3, and 5, since 30 can be expressed as 2 × 3 × 5.

2. Composite Factors

Unlike prime factors, composite factors are numbers that have more than two factors. These are essentially non-prime numbers (excluding 1) that can divide another number completely.

• Characteristics: Composite factors are greater than 1 and have at least one divisor other than 1 and themselves.
• Example: The composite factors of 18 are 6 and 9, as both of these numbers have divisors other than 1 and themselves and can divide 18 without a remainder.

3. Positive and Negative Factors

Every positive number has both positive and negative factors. The positive factors are the numbers that can divide the given number without leaving a remainder, while the negative factors are simply the negative counterparts of these positive factors.

• Characteristics: For every positive factor ‘a’ of a number ‘b’, there exists a corresponding negative factor ‘-a’.
• Example: The positive factors of 5 are 1 and 5, while the negative factors are -1 and -5.

Factors of Prime VS Composite Numbers

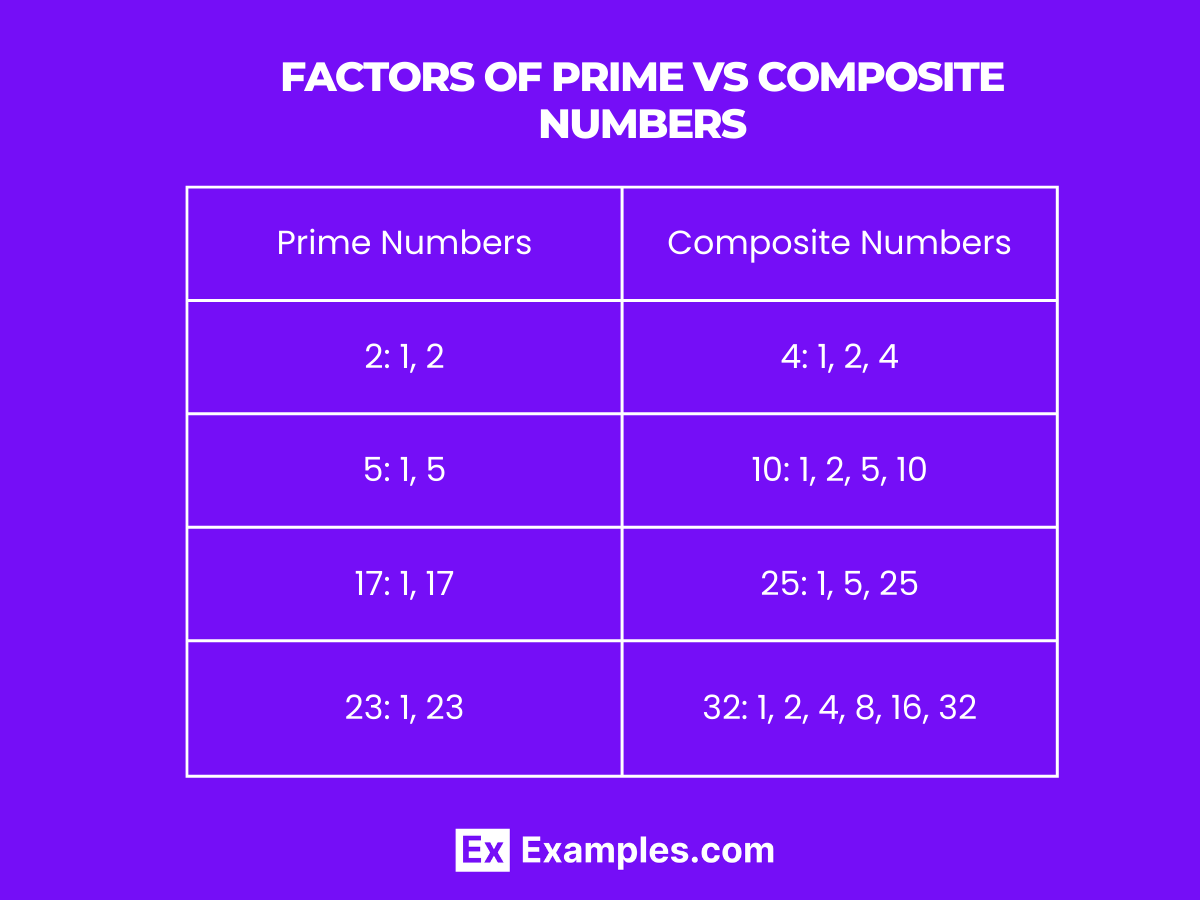
Prime Numbers	Composite Numbers
2: 1, 2	4: 1, 2, 4
5: 1, 5	10: 1, 2, 5, 10
17: 1, 17	25: 1, 5, 25
23: 1, 23	32: 1, 2, 4, 8, 16, 32

Prime Factorization

Prime factorization is the method of breaking down a number into its constituent prime numbers, which, when multiplied together, result in the original number. This process involves dividing the number by the smallest prime numbers until the number is reduced to 1.

For instance, let’s consider the prime factorization of 18:

1. Start with the smallest prime number, 2. Since 18 is divisible by 2, one of the prime factors is 2.18÷2=9
2. Now, we have 9, which is not divisible by 2, so we move to the next prime number, 3. Since 9 is divisible by 3, another prime factor is 3.9÷3=3
3. We’re left with 3, which is a prime number itself, so it’s also a prime factor.

Thus, the prime factorization of 18 is 2×3×3

Solved Problems on Factors

Understanding the concept of factors in mathematics is crucial for grasping the basics of number theory, which further aids in solving various mathematical problems. Factors of a number refer to whole numbers that can evenly divide the given number without leaving a remainder. In this comprehensive guide, we’ll explore a few solved problems on factors to enhance your understanding and proficiency in dealing with such mathematical challenges.

1. Finding Factors of 24

To find the factors of 24, we look for all the whole numbers that can divide 24 evenly. Starting from 1 (since 1 is a factor of every number), we test each number up to 24 to see if it divides without leaving a remainder.

1. 1 × 24 = 24
   1 and 24 are factors of 24 because when multiplied, they result in 24.
2. 2 × 12 = 24
   2 and 12 are factors of 24 because they evenly divide the number without a remainder.
3. 3 × 8 = 24
   3 and 8 are factors of 24, further proving the point with their product equating to 24.
4. 4 × 6 = 24
   Lastly, 4 and 6 are also factors of 24, as they divide 24 evenly.

The factors of 24 are 1, 2, 3, 4, 6, 8, 12, and 24.

2. Finding Factors of 36

To find the factors of 36, we will go through all whole numbers from 1 to 36 and check which ones can divide 36 without leaving a remainder.

1. 1 × 36 = 36
   1 and 36 are automatically factors of 36.
2. 2 × 18 = 36
   2 and 18 are factors of 36 because their product equals 36.
3. 3 × 12 = 36
   3 and 12 evenly divide 36, making them factors as well.
4. 4 × 9 = 36
   4 and 9 are also factors of 36 since they divide the number evenly.
5. 6 × 6 = 36
   6 is a factor as well, and in this case, it’s repeated because 6 times itself equals 36.

The factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18, and 36.

3. Finding Factors of 15

To identify the factors of 15, we will examine each whole number from 1 to 15 to see if it can divide 15 without a remainder.

1. 1 × 15 = 15
   1 and 15 are factors of 15 since their multiplication results in 15.
2. 3 × 5 = 15
   3 and 5 are factors of 15 as they divide the number evenly.

The factors of 15 are 1, 3, 5, and 15.

Real life Applications on  Prime Factorization

When organizing a bookshelf with a collection of books from various series, prime factorization can assist in arranging them in a way that maximizes accessibility and aesthetic appeal. Suppose you have 60 books comprising several series, and you want to organize them into equal sections without mixing the series.

By applying prime factorization to the total number of books (60), we find its prime factors are 2, 2, 3, and 5 (or 22×3×522×3×5). This gives us several options for dividing the books into equal sections: 2 sections of 30, 3 sections of 20, 4 sections of 15, 5 sections of 12, 6 sections of 10, and so on.

Using these factors, you can decide how to group the books.

In Conclusion, Understanding factors in mathematics enriches our grasp of number properties, highlighting the distinctions between prime and composite numbers. Proper factors, excluding the number itself, and the balance of positive and negative factors, provide a comprehensive view of a number’s divisibility. These concepts lay the foundation for deeper mathematical exploration and problem-solving.
<br/>