Midpoint Calculator

Find the midpoint between two points effortlessly with the Examples.com Midpoint Calculator. Get precise results quickly.

How to Use Midpoint Calculator

To use the midpoint calculator as shown in the screenshot, follow these steps:

Step 1: Enter the Coordinates of the First Point

• In the ‘First Point Coordinates’ section, input the x-coordinate (x1) in the first field.
• Enter the y-coordinate (y1) in the second field next to it.

Step 2: Enter the Coordinates of the Second Point

• Move to the ‘Second Point Coordinates’ section.
• Input the x-coordinate (x2) for the second point in the first field.
• Enter the y-coordinate (y2) for the second point in the adjacent field.

Step 3: Calculate the Midpoint

• Once both points’ coordinates are entered, the calculator automatically calculate the midpoint. If it doesn’t, look for a button labeled ‘Calculate’, ‘Find Midpoint’, or a similar command, and click it.

Step 4: View the Midpoint Result

• The ‘Midpoint Coordinates’ section will display the x and y values of the midpoint (xmidpoint and ymidpoint).
• These values are the average of the x-coordinates and the y-coordinates of the two points, respectively.

Step 5: Clear if Necessary

• If you wish to perform another calculation, you can use the ‘Clear’ button to reset all fields.

How to Calculate the Midpoint

To calculate the midpoint between two points using a midpoint calculator, follow these steps:

Step 1: Determine the Coordinates of Your Points

Identify the coordinates (x₁, y₁) for the first point and (x₂, y₂) for the second point. You need both the x (horizontal) and y (vertical) values for each point.

Step 2: Access the Midpoint Calculator

Open the midpoint calculator. This could be an online tool or a function on your scientific calculator.

Step 3 : Enter the Coordinates

• Find the input fields for the first point’s coordinates.
• Enter the x₁ value in the field labeled for the first point’s x-coordinate.
• Enter the y₁ value in the field labeled for the first point’s y-coordinate.
• Move to the input fields for the second point’s coordinates.
• Enter the x₂ value in the field labeled for the second point’s x-coordinate.
• Enter the y₂ value in the field labeled for the second point’s y-coordinate.

Step 4: Initiate the Calculation

Click the button that usually says “Calculate”, “Compute”, or something similar. If the calculator is automatic, it may compute the midpoint as soon as you’ve entered all the coordinates.

Step 5: Review the Midpoint

The calculator will display the midpoint coordinates, often labeled as (xₘ, yₘ). The midpoint coordinates are calculated as follows:

x_m​= (x_1​+x_2​)​ ÷ 2

y_m​= (y₁+y₂) ÷ 2

The result is the average of the x-coordinates and the y-coordinates, giving you the exact middle point along the straight line that connects the two points.

Step 6: Use the Result

You can now use the calculated midpoint coordinates for further calculations or for graphical representations.

Calculating the midpoint is a common task in mathematics, especially in geometry, when finding the center point is needed for constructing bisectors, analyzing shapes, or plotting on a graph

Midpoint Formula

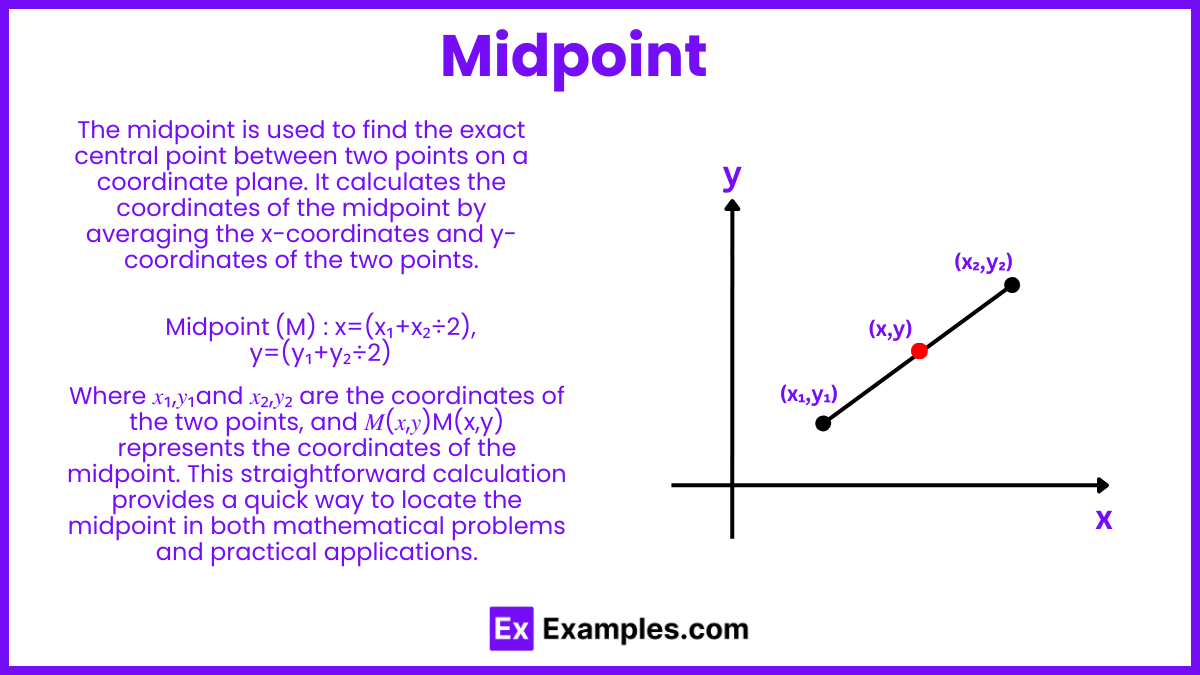
The midpoint formula is used to find the point that is exactly halfway between two given points in a plane. The formula is:

Midpoint (M)=(x₁​+x₂÷2​​, y₁​+y₂÷2​​)

Where:

• (x₁​,y_1​) are the coordinates of the first point,
• (x_2​,y₂​) are the coordinates of the second point,
• M is the midpoint.

This formula gives you the coordinates of the midpoint M, which are the averages of the x-coordinates and the y-coordinates of the two points, respectively.

Examples of Midpoint

Example 1:

Given two points A(2, 4) and B(6, 8), find the midpoint.

Midpoint =(2+6÷2,4+8÷2)=(4,6)

Example 2:

Find the midpoint between points P(-3, 5) and Q(7, -1).

Midpoint =(−3+7÷2,5+(−1)÷2)=(2,2)

Example 3:

Calculate the midpoint for points X(0, 0) and Y(10, 10).

Midpoint =(0+10÷2,0+10÷2)=(5,5)

Example 4:

Given points R(-5, -3) and S(3, 7), determine the midpoint.

Midpoint =(−5+3÷2,−3+7÷2)=(−1,2)

Example 5:

Find the midpoint between points T(4, -2) and U(-6, 8).

Midpoint =(4+(−6)÷2,−2+8÷2)=(−1,3)

Midpoints in Geometry

In geometry, the midpoint of a line segment is the point that divides the segment into two equal parts. It’s exactly halfway between the endpoints of the segment. If you have a line segment with endpoints at coordinates (x₁​,y₁​) and (x_2​,y₂​), the midpoint (M) can be calculated using the midpoint formula:

M=(x₁​+x₂÷2​​,y_1​+y_2​​÷2)

This formula provides the average of the x-coordinates and the y-coordinates of the endpoints, giving the exact center point. Midpoints are widely used in both theoretical geometry and practical applications, such as engineering and design.

What is the midpoint between points A and B?

The midpoint between two points, A and B, is a point that is exactly halfway between them on the straight line segment that joins these points. It divides the line segment into two equal parts. If A has coordinates (x1, y1) and B has coordinates (x2, y2), the midpoint, M, can be calculated using the formula: M=(x₁​+x₂÷2​​,y_1​+y_2​​÷2)

Does a midpoint have to be in the middle?

Yes, a midpoint must always be in the middle of a line segment. It is defined as the point that equally divides the segment into two halves, ensuring that each half is of equal length.

Can there be two midpoints?

No, there can only be one midpoint for a straight line segment. By definition, the midpoint is the single point that divides the segment into two equal parts. Having more than one would contradict the definition of a midpoint.

Does midpoint mean both sides are equal?

Yes, the term “midpoint” implies that both sides of the line segment are equal in length. The midpoint is the point that splits the segment into two equal parts, each with the same length from the midpoint to each endpoint.

Does a line have exactly one midpoint?

A line segment has exactly one midpoint. However, an infinite line does not have a midpoint since it extends indefinitely in both directions, making it impossible to determine a central point.