Number Lines – Parts, Importance, Types, Tools

Mathematical journey with our definitive guide to number lines, an essential tool for educators and students. This resource demystifies number lines, illustrating their importance in understanding the fundamentals of mathematics. Through practical examples and straightforward explanations, we aim to enhance numerical literacy, providing learners with the skills needed to tackle a wide range of mathematical challenges. Whether used for simple addition or complex algebra, this guide ensures number lines are accessible and engaging for all.

What are Number Lines?

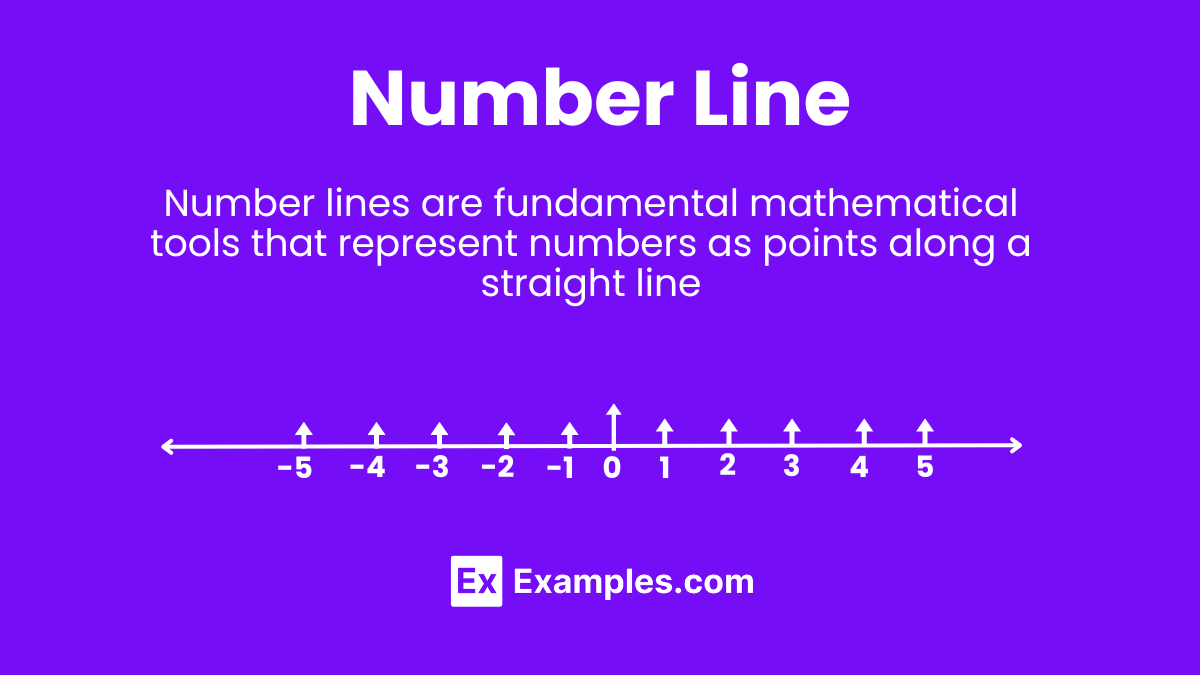
Number lines are fundamental mathematical tools that represent numbers as points along a straight line. Each point corresponds to a number, with equal intervals indicating equal value differences. They serve as a visual aid to understand concepts such as addition, subtraction, and other operations, making abstract ideas tangible. By incorporating number lines into lessons, teachers can significantly improve students’ comprehension of numerical relationships and mathematical reasoning.

What is the Best Example of a Number Line?

The best example of a number line is its use in visualizing addition and subtraction. For instance, to add 2 + 3, start at the point labeled 2, move three units to the right, and arrive at 5. Conversely, to subtract 3 from 5, start at 5 and move three units to the left, landing on 2. This visual method simplifies these operations, making it easier for students to grasp the concept of movement along the number line, thereby enhancing their mathematical understanding and skills.

How to Draw a Number Line?

Mastering how to draw a number line is pivotal for both educators and students, facilitating a deeper understanding of mathematical concepts. This guide outlines the simple steps to create a number line: start with a straight line, mark a point for zero, and evenly space increments both to the right for positive numbers and to the left for negative numbers. This visual tool is indispensable in teaching numerical order, addition, subtraction, and introducing the concept of integers, making math more accessible and engaging.

Examples:

1. Creating a Basic Number Line:
   • Draw a horizontal line and evenly space marks along it. Label the center as 0, marks to the right with positive numbers, and to the left with negative numbers.
2. Adding Intervals:
   • On your number line, decide on the interval (e.g., 1s, 2s, 5s) and mark accordingly. This helps in understanding scale and distance between numbers.
3. Including Fractions:
   • For a more advanced number line, between any two whole numbers, add marks for fractions or decimals to illustrate these concepts visually.
4. Incorporating Colored Segments:
   • Use different colors to highlight sections of the number line, such as positive and negative areas, to enhance comprehension of number relationships.
5. Interactive Number Line:
   • Create a number line with movable markers or labels to allow students to physically engage with addition, subtraction, and number placement exercises.

Negative and Positive Number Line

A negative and positive number line visually represents both negative and positive integers on either side of zero, serving as a fundamental tool in mathematics for illustrating the concept of opposites. It aids in teaching the addition and subtraction of negative numbers, understanding absolute values, and exploring the relationships between numbers. This dual-sided approach not only simplifies complex concepts but also enriches students’ numerical fluency and analytical skills, making it an essential element in math education.

Examples:

1. Understanding Zero’s Role:
   • The point where the negative side transitions to the positive, zero serves as a central reference, emphasizing its importance as neither positive nor negative.
2. Comparing Temperatures:
   • Use a number line to compare temperatures below and above freezing, illustrating how negative numbers represent colder temperatures than zero.
3. Elevation Above and Below Sea Level:
   • Depict elevations using a number line, where positive numbers indicate above sea level and negative numbers represent below sea level, making abstract concepts tangible.
4. Financial Balances:
   • A number line can demonstrate financial concepts, such as debts (negative values) versus savings (positive values), providing real-world applications.
5. Time Zones:
   • Illustrate time differences from a reference point (e.g., GMT) using a number line, with eastward zones as positive and westward as negative.

Parts of a Number Line

Understanding the parts of a number line is crucial for students to navigate and apply mathematical concepts effectively. A number line consists of a horizontal line marked with numbers at equal intervals, a zero point that divides the line into positive and negative sides, and often includes tick marks or points to represent specific numbers or values. By dissecting a number line into its component parts, educators can guide students through various mathematical operations and principles, enhancing their grasp of linear measurements, operations, and number properties.

Examples:

1. Zero Point:
   • The central point of a number line, dividing positive and negative values, crucial for understanding the concept of polarity in numbers.
2. Intervals:
   • Regularly spaced marks that indicate the distance between numbers, essential for measuring and calculating differences or sums.
3. Positive Side:
   • The right side of zero, representing positive numbers, crucial for understanding growth, addition, and positive changes.
4. Negative Side:
   • The left side of zero, showcasing negative numbers, vital for depicting reductions, subtraction, and debts.
5. Tick Marks:
   • Small lines used to represent individual numbers, helping users precisely identify and locate specific values on the number line.

Each component plays a significant role in utilizing number lines as educational tools, facilitating a comprehensive understanding of numerical concepts and their applications.

Number Line 1 to 100

Number Line with Decimals

Dive into the precision of mathematics with our guide on number lines with decimals. This tool is pivotal for teachers and students to understand fractions and decimals visually. It breaks down complex concepts, making them easier to grasp by illustrating the values between whole numbers. By placing decimals accurately on the number line, learners can compare and perform operations with decimals, enhancing their mathematical fluency and confidence in handling real-world problems.

Examples:

1. Placing 0.5 on the Number Line:
   • Locate 0.5 between 0 and 1, showing how decimals represent values less than a whole. This illustrates the concept of halves, foundational for understanding fractions and decimals.
2. Comparing 0.75 and 0.25:
   • By marking 0.75 and 0.25 on the number line, students visually understand that 0.75 is closer to 1, emphasizing the idea of quarter values and their comparison.
3. Adding Decimals: 0.3 + 0.6:
   • Start at 0.3, move 0.6 units to the right, and land on 0.9. This example teaches adding decimals, providing a clear visual representation of the sum.
4. Subtracting Decimals: 0.8 – 0.3:
   • From the point 0.8, move 0.3 units to the left to reach 0.5. Demonstrates subtraction of decimals, reinforcing the concept through visual aids.
5. Finding Midpoints: Between 0.2 and 0.4:
   • Identifying the midpoint at 0.3 showcases how number lines can determine values exactly between two decimals, fostering a deeper understanding of number relationships.

Inequalities on a Number Line

Explore the realm of inequalities through our insightful guide on representing them on a number line. Ideal for educators aiming to demystify algebraic concepts, this resource uses number lines to visually express inequalities, making abstract concepts tangible. Students learn to plot and interpret inequalities, gaining a solid foundation in understanding mathematical relationships. This visual approach not only clarifies the nature of inequalities but also prepares learners for more complex algebraic reasoning and problem-solving.

Examples:

1. Plotting x > 2:
   • Draw an open circle at 2 and shade the line to the right, indicating all values greater than 2. This visual helps students grasp the concept of greater-than inequalities.
2. Representing x ≤ -1:
   • Place a closed circle at -1 and shade to the left, showing x is less than or equal to -1. It visually demonstrates how to include the endpoint in the solution set.
3. Graphing x < 3:
   • An open circle at 3 with shading to the left illustrates values less than 3, teaching students about less-than inequalities and their graphical representations.
4. Illustrating x ≥ 0.5:
   • With a closed circle at 0.5 and shading to the right, students see that x is any value greater than or equal to 0.5, emphasizing the equality component of inequalities.
5. Solving Compound Inequalities: 1 < x ≤ 4:
   • Plot an open circle at 1 and a closed circle at 4, shading between them. This teaches the concept of compound inequalities, showing values that x can take within a range.

These detailed explanations and examples for number lines with decimals and inequalities on a number line are crafted to enhance the learning experience, providing teachers and students with effective tools to master mathematical concepts.

Graphing Inequalities on a Number Line

Graphing inequalities on a number line offers a visual representation to solve and understand inequalities. This method highlights the range of values that satisfy the inequality, using open or closed circles to indicate whether endpoints are included. By incorporating this technique, educators can enhance students’ comprehension of mathematical concepts, providing a clear and intuitive way to grasp inequalities.

Examples:

1. Less Than Five (x < 5):
   • Use an open circle at 5 and shade left to represent all numbers less than 5, illustrating values not reaching 5.
2. Greater Than or Equal to Three (x ≥ 3):
   • Place a closed circle at 3 and shade right, indicating inclusivity of 3 and all numbers greater than 3.
3. Not Equal to Two (x ≠ 2):
   • An open circle at 2 with no shading demonstrates that all numbers are valid except 2, emphasizing exclusion.
4. Between One and Four (1 < x < 4):
   • Open circles at 1 and 4 with shading between them show values strictly between 1 and 4, excluding endpoints.
5. At Most Six (x ≤ 6):
   • A closed circle at 6 shaded leftward indicates all numbers up to and including 6 are solutions, showing inclusivity.

The Importance of Number Lines

Number lines are invaluable in education, offering a straightforward method for visualizing and understanding numerical concepts. They aid in the comprehension of basic operations, inequalities, and absolute values, fostering a deep understanding of mathematical principles. By integrating number lines into teaching, educators can simplify complex ideas, making mathematics more accessible and less intimidating for students.

Examples:

1. Understanding Absolute Value:
   • Demonstrating distance from zero on a number line helps clarify the concept of absolute value, making it tangible.
2. Simplifying Fraction Comparison:
   • Placing fractions on a number line allows for easy comparison, enhancing understanding of their relative sizes.
3. Visualizing Integer Operations:
   • Using number lines to add or subtract integers provides a clear visual path of movement, aiding in operation comprehension.
4. Decimals and Place Value:
   • Number lines illustrate how decimals fit between integers, clarifying the concept of place value and decimal positions.
5. Concept of Negative Numbers:
   • Introducing negative numbers on a number line helps students grasp the idea of values less than zero, expanding their number sense.

Different Types of Numbers on a Number Line

Number lines can represent a variety of number types, including integers, fractions, decimals, and even irrational numbers. This versatility makes number lines a powerful tool for teaching a broad spectrum of mathematical concepts. Understanding how different types of numbers are positioned on a number line enhances students’ numerical fluency and mathematical reasoning.

Examples:

1. Integers:
   • Marked at regular intervals, integers on a number line show the progression of whole numbers, including negatives.
2. Fractions:
   • Fractions are positioned between integers, illustrating their values in relation to whole numbers and each other.
3. Decimals:
   • Decimals appear between integers and fractions, demonstrating their precise value and helping compare decimal quantities.
4. Irrational Numbers:
   • While not marked exactly, irrational numbers’ approximate locations can be shown, bridging gaps between rational numbers.
5. Real Numbers:
   • A number line represents the continuum of real numbers, encompassing all rational and irrational numbers within its span.

Number Lines as Mathematical Tools

Number lines are essential mathematical tools that facilitate the understanding of numerical relationships and operations. They serve as the foundation for developing algebraic thinking, enabling students to visualize and solve equations, understand functions, and explore the properties of numbers. By using number lines, educators can create a dynamic learning environment that encourages exploration and enhances students’ mathematical intuition.

Examples:

1. Solving Equations:
   • Demonstrating solutions to simple equations on a number line helps students understand the concept of equality and balance.
2. Exploring Functions:
   • Graphing functions on a number line can introduce the idea of change and rate, foundational for algebraic concepts.
3. Understanding Sequences:
   • Visualizing arithmetic and geometric sequences on a number line aids in recognizing patterns and relationships between terms.
4. Coordinate Geometry:
   • Number lines lay the groundwork for understanding coordinates, crucial for graphing and spatial reasoning in geometry.
5. Probability and Statistics:
   • They can represent probability distributions and statistical data, providing a basis for understanding randomness and variation.

Number lines stand as a fundamental tool in the realm of mathematics, bridging the gap between abstract concepts and visual understanding. By facilitating a deeper comprehension of numerical relationships, operations, and inequalities, they empower educators to deliver lessons that enhance students’ analytical skills and confidence in math. Incorporating number lines into educational practices promises to enrich the learning experience and foster a lifelong appreciation for mathematics.