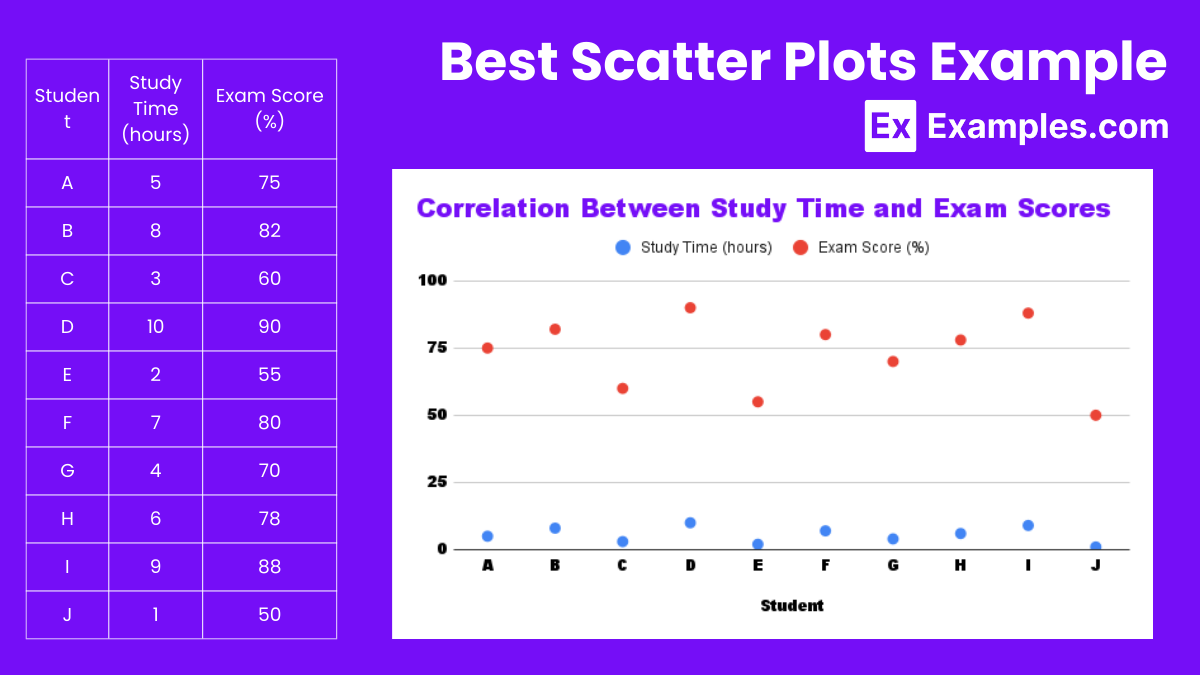
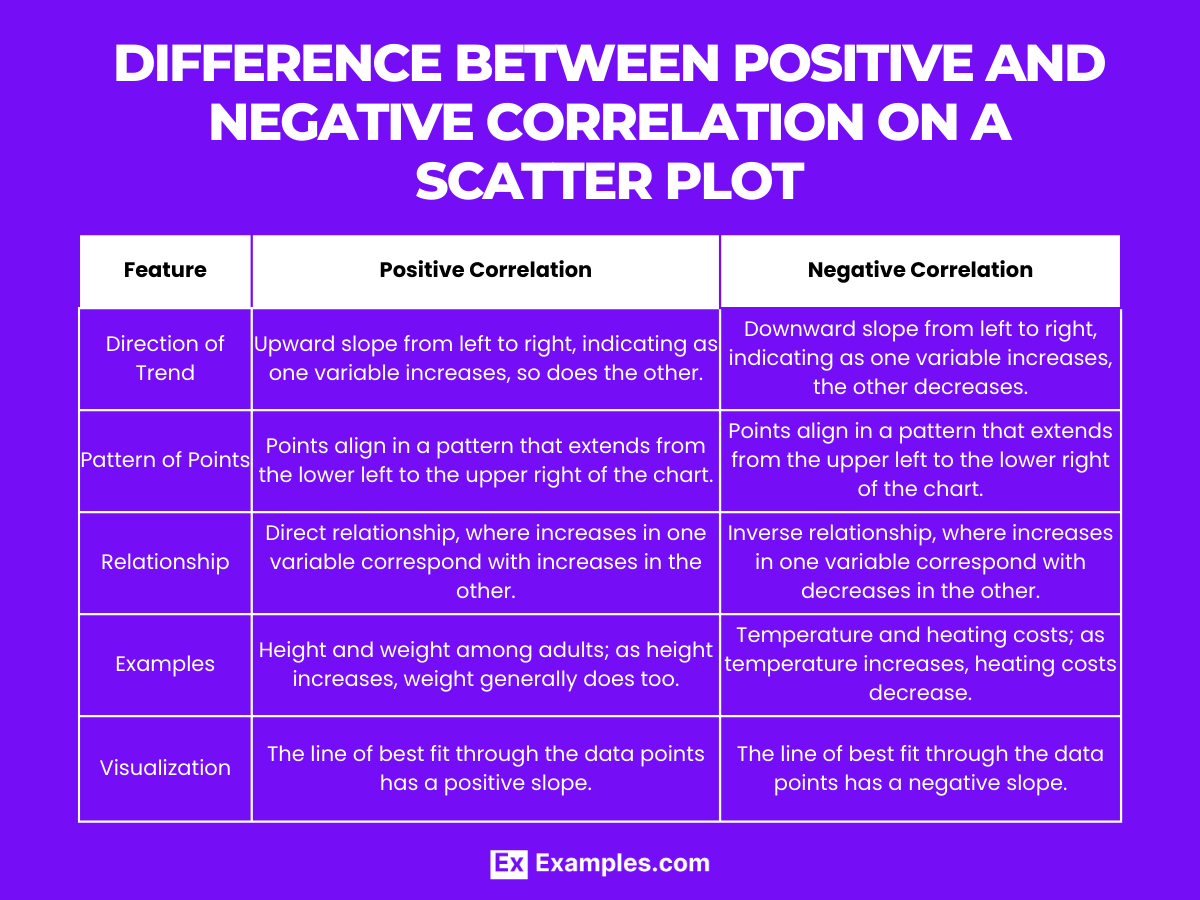
Which of the following scatter plots represents a positive correlation?
A plot where the points slope downward from left to right
A plot where the points slope upward from left to right
A plot where the points are scattered randomly
A plot where the points form a vertical line