Determining Volume with Cross-Sections, the Disc Method, and the Washer Method

In both AP Calculus AB and BC, determining the volume of solids is a crucial concept. This involves calculating volumes using various methods like cross-sections, the disc method, and the washer method. These techniques allow students to find the volume of solids generated by rotating a region around an axis or by slicing the solid into known cross-sectional shapes. Mastery of these methods is essential for success in the AP Calculus exams, as they are commonly tested and foundational in understanding integral applications.

Learning Objectives

By studying the topic “Determining Volume with Cross-Sections, the Disc Method, and the Washer Method” for the AP Calculus AB and BC exams, you should aim to master calculating volumes of solids formed by rotating regions around an axis or by slicing perpendicular cross-sections. You will learn to set up and evaluate integrals for these methods, understand when to apply each technique, and interpret geometric properties of solids. This knowledge is essential for solving complex volume problems on the AP Calculus exam.

Volume with Cross-Sections

When finding the volume of a solid using cross-sections, you essentially slice the solid into thin, parallel slices perpendicular to an axis. The area of each slice is calculated, and then these areas are integrated over the interval that the slices span.

Steps to Determine Volume

• Identify the Shape of the Cross-Section: Depending on the problem, the cross-section might be a square, rectangle, semicircle, triangle, or another shape. The shape will determine the formula for the area.
• Express the Area as a Function of x (or y): Write the area of a typical cross-section as a function of the variable of integration (usually x or y).
• Set Up the Integral: Integrate the area function over the interval that corresponds to the base of the solid.
• Evaluate the Integral: Compute the definite integral to find the volume.

Example Problem

Consider a solid where the cross-sections perpendicular to the x-axis are squares, and the base of the solid lies between x=0 and x=2 on the x-axis with the top curve given by y = x².

• Step 1: Identify the cross-section as a square.
• Step 2: The side length of the square is s = x².
• Step 3: The area A(x) of the square is A(x) = (x²)² = x⁴.
• Step 4: Set up the integral for the volume V: \(V = \int_{0}^{2} x^4 \, dx \)
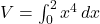
• Step 5: Evaluate the integral: \(V = \left[ \frac{x^5}{5} \right]_{0}^{2} = \frac{32}{5} = 6.4 \text{ cubic units} \)

Volume with the Disc Method

The Disc Method is used to find the volume of a solid of revolution when a region is revolved around a horizontal or vertical axis. This method applies when the solid has no hole (i.e., it’s completely solid).

Steps to Determine Volume

• Sketch the Region: Determine the region being revolved and the axis of revolution.
• Express the Radius of the Disc: If the region is revolved around the x-axis, the radius is the distance from the x-axis to the curve, which is simply the function y = f(x). If revolved around the y-axis, the radius will be x=g(y).
• Set Up the Integral: The area of a disc is 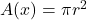\(A(x) = \pi r^2\). Integrate this area across the bounds of the region.
• Evaluate the Integral: Compute the integral to find the volume.

Example Problem

Find the volume of the solid obtained by revolving the region under the curve \(y = \sqrt{x}\) from x = 0 to x = 4 about the x-axis.

• Step 1: Sketch the region and note the curve \(y = \sqrt{x}\)​.
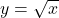• Step 2: The radius r(x) of each disc is \(r(x) = \sqrt{x}\).
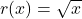• Step 3: The area of each disc is \(A(x) = \pi (\sqrt{x})^2 = \pi x\).
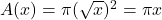• Step 4: Set up the integral for the volume V: \(V = \int_{0}^{4} \pi x \, dx \)
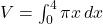
• Step 5: Evaluate the integral: \(V = \pi \left[ \frac{x^2}{2} \right]_{0}^{4} = \pi \times 8 = 8\pi \text{ cubic units}\)

Volume with the Washer Method

The Washer Method extends the Disc Method to situations where the solid has a hole in the middle, like a donut or washer. This occurs when a region between two curves is revolved around an axis.

Steps to Determine Volume

• Sketch the Region: Identify the region and note the inner and outer curves.
• Express the Radii: Determine the outer radius R(x) and inner radius r(x). These represent the distance from the axis of revolution to the outer and inner curves, respectively.
• Set Up the Integral: The volume of a washer is found by subtracting the area of the inner disc from the outer disc: \(A(x) = \pi [R(x)^2 – r(x)^2]\) Integrate this over the interval of the region.
• Evaluate the Integral: Compute the integral to find the volume.

Example Problem

Find the volume of the solid formed by revolving the region between the curves y = x² and y = x about the x-axis, from x = 0 to x = 1.

• Step 1: Sketch the region between the curves y = x (outer curve) and y = x² (inner curve).
• Step 2: The outer radius R(x) is R(x) = x, and the inner radius r(x) is r(x) = x².
• Step 3: The area of each washer is \(A(x) = \pi [(x)^2 – (x^2)^2] = \pi [x^2 – x^4]\).
• Step 4: Set up the integral for the volume V: \(V = \int_{0}^{1} \pi [x^2 – x^4] \, dx \)
• Step 5: Evaluate the integral: \(V = \pi \left[ \frac{x^3}{3} – \frac{x^5}{5} \right]_{0}^{1} = \pi \left(\frac{1}{3} – \frac{1}{5}\right) = \frac{2\pi}{15} \text{ cubic units} \)

Key Tips for AP Calculus Exam Success

• Understand the Problem: Visualizing the region and sketching it can help immensely in setting up the problem correctly.
• Know When to Use Each Method:
  • Cross-Sections: Use when given specific cross-sectional shapes.
  • Disc Method: Use when the solid is solid throughout (no hole).
  • Washer Method: Use when there’s a hole or gap between the region and the axis of rotation.
• Practice Setting Up Integrals: The biggest challenge is often in correctly setting up the integral, especially determining the correct bounds and expressions for radii.
• Check Units and Limits: Always check that your units make sense (cubic units for volume) and that your limits of integration correspond to the correct region.

Examples

Example 1: Volume of a Solid with Square Cross-Sections

Consider a solid whose base is the region between the curves y = sin(x) and y = 0 on the interval [0,π]. The cross-sections perpendicular to the x-axis are squares. The side length of each square is s(x) = sin(x). Therefore, the area of the cross-section is A(x) = s(x)² = sin²(x). The volume of the solid is calculated as \( V = \int_{0}^{\pi} \sin^2(x) \, dx \). This integral can be solved using trigonometric identities and integration techniques, yielding the final volume.

Example 2: Volume of a Solid of Revolution Using the Disc Method

Find the volume of the solid formed by revolving the region bounded by y = x² and y = 0 around the x-axis from x = 0 to x = 2. The radius of each disc is given by R(x) = x², so the volume is \( V = \pi \int_{0}^{2} (x^2)^2 \, dx = \pi \int_{0}^{2} x^4 \, dx \). Solving the integral gives the volume \( V = \frac{32\pi}{5} \)​ cubic units.

Example 3: Volume Using the Washer Method with Vertical Rotation

Determine the volume of the solid obtained by revolving the region bounded by y = x​ and y = x around the y-axis from y = 0 to y = 1. Here, the outer radius \( R_{\text{outer}}(y) = \frac{1}{y^2} \)​ and the inner radius Rinner​ \( R_{\text{inner}}(y) = y \). The volume is found using \( V = \pi \int_{0}^{1} \left[\left(\frac{1}{y^2}\right)^2 – y^2\right] dy \), which simplifies and integrates to give the volume of the solid.

Example 4: Volume of a Solid with Semicircular Cross-Sections

A solid has a base defined by the interval [0,2] on the x-axis and cross-sections perpendicular to the x-axis that are semicircles. The diameter of each semicircle is the distance between the curves y = x² and y = 0. The area of each semicircular cross-section is \( A(x) = \frac{1}{2} \pi \left(\frac{x^2}{2}\right)^2 \). The volume of the solid is then \( V = \int_{0}^{2} \frac{1}{2} \pi \left(\frac{x^2}{2}\right)^2 dx \), which, upon evaluation, gives the total volume.

Example 5: Volume of a Solid of Revolution Using the Washer Method with Horizontal Rotation

Consider the region bounded by y = x² and y = 4 on the interval [0,2]. When this region is revolved around the y-axis, the solid formed has a hole in the middle, so we use the washer method. The outer radius Router​(y) = 2 and the inner radius \( R_{\text{inner}}(y) = \sqrt{y} \). The volume of the solid is \( V = \pi \int_{0}^{4} \left(4 – y\right) dy \). After solving the integral, the volume of the solid can be calculated.

Multiple Choice Questions

Question 1

Which of the following integrals correctly represents the volume of the solid obtained by revolving the region bounded by y = x² and y = 0 about the x-axis from x = 0 to x = 3?

A) \( V = \int_{0}^{3} \pi x^2 \, dx \)
B) \( V = \pi \int_{0}^{3} x^4 \, dx \)
C) \( V = 2\pi \int_{0}^{3} x^2 \, dx \)
D) \( V = \pi \int_{0}^{3} \left(\sqrt{x}\right)^2 \, dx \)

Correct Answer: B) \( V = \pi \int_{0}^{3} x^4 \, dx \)

Explanation:

The solid is formed by revolving the region under the curve y = x² around the x-axis. The radius R(x) of each disc is equal to y = x². The volume of the solid is given by the disc method formula \( V = \pi \int_{a}^{b} [R(x)]^2 \, dx \). Substituting R(x) = x², we get the integral \( V = \pi \int_{0}^{3} (x^2)^2 \, dx = \pi \int_{0}^{3} x^4 \, dx \).

Question 2

Consider a solid formed by revolving the region bounded by y = x​ and y = x about the y-axis. Which of the following expressions represents the volume of this solid?

A) \( V = \pi \int_{0}^{1} \left( \sqrt{y} – y \right)^2 \, dy \)
B) \( V = \pi \int_{0}^{1} \left( \frac{1}{\sqrt{y}} – y \right)^2 \, dy \)
C) \( V = \pi \int_{0}^{1} \left( \frac{1}{y} – y^2 \right) \, dy \)
D) \( V = \pi \int_{0}^{1} \left( \frac{1}{y} – y^2 \right)^2 \, dy \)

Correct Answer: D) \( V = \pi \int_{0}^{1} \left( \frac{1}{y} – y^2 \right)^2 \, dy \)

Explanation:

When revolving the region around the y-axis, we use the washer method because the region is bounded by two curves. The outer radius is given by the curve \( x = \frac{1}{y} \) (which corresponds to \( y = \frac{1}{\sqrt{x}} \)), and the inner radius is x = y² (since \( y = \sqrt{x} \)​). The volume is given by \( V = \pi \int_{a}^{b} \left( R_{\text{outer}}(y)^2 – R_{\text{inner}}(y)^2 \right) dy \). Substituting the appropriate expressions for the radii, we get \( V = \pi \int_{0}^{1} \left( \frac{1}{y} – y^2 \right)^2 \, dy \).

Question 3

What is the volume of the solid formed by revolving the region between y = x² and y = 2x around the x-axis from x = 0 to x = 2?

A) \( V = \pi \int_{0}^{2} (2x)^2 \, dx \)
B) \( V = \pi \int_{0}^{2} \left[(2x)^2 – (x^2)^2\right] \, dx \)
C) \( V = \pi \int_{0}^{2} \left[(2x)^2 – (x^2)\right] \, dx \)
D) \( V = \pi \int_{0}^{2} \left[(2x) – (x^2)\right]^2 \, dx \)

Correct Answer: C) \( V = \pi \int_{0}^{2} \left[(2x)^2 – (x^2)\right] \, dx \)

Explanation:

The solid is formed by revolving the region bounded by the curves y = x² and y = 2x around the x-axis. The washer method is applicable because there is an inner radius Rinner​(x) = x² and an outer radius Router​(x) = 2x. The volume is given by \( V = \pi \int_{a}^{b} \left( R_{\text{outer}}(x)^2 – R_{\text{inner}}(x)^2 \right) dx \). Plugging in the given functions, the correct integral expression is \( V = \pi \int_{0}^{2} \left[(2x)^2 – (x^2)\right] \, dx \).