Identifying Asymptotes of and Holes in the Graphs of Rational Functions
In AP Precalculus, identifying asymptotes and holes in the graphs of rational functions is crucial for understanding the function’s behavior. Asymptotes are lines that the graph approaches but never touches, helping to define the end behavior. Vertical asymptotes occur where the denominator equals zero, while horizontal asymptotes depend on the degrees of the numerator and denominator. Holes, on the other hand, appear where common factors cancel out. Mastering these concepts is essential for analyzing and graphing rational functions accurately in calculus and advanced mathematics.
Learning Objectives
In the topic of “Identifying Asymptotes of and Holes in the Graphs of Rational Functions” for AP Precalculus, you should focus on understanding how to determine vertical and horizontal asymptotes by analyzing the degrees of the numerator and denominator, as well as factoring the function to identify holes. You should be able to locate vertical asymptotes where the denominator equals zero (unless canceled) and analyze the function’s behavior at infinity for horizontal asymptotes. Additionally, learn to identify and calculate the coordinates of holes when common factors cancel out.
Identifying Asymptotes of and Holes in the Graphs of Rational Functions
Rational functions are functions of the form \( f(x) = \frac{p(x)}{q(x)} \), where p(x) and q(x) are polynomials, and \( q(x) \neq 0 \). To analyze the behavior of rational functions, it is crucial to identify the vertical and horizontal asymptotes, as well as any holes in the graph.
Vertical Asymptotes (VAs)
Vertical asymptotes occur at the values of x where the denominator of the rational function equals zero, provided that these values do not result in a hole.
- To find the vertical asymptotes:
- Set the denominator equal to zero: q(x)=0.
- Solve for x.
- If the solution results in a value that cancels out with a corresponding factor in the numerator, then it indicates a hole, not a vertical asymptote.
- If it doesn’t cancel, the solution represents a vertical asymptote.
Example: \( f(x) = \frac{(x – 2)}{(x – 3)(x + 1)} \).
- Set (x−3) (x+1) = 0, which gives x = 3 and x = −1.
- Both values result in vertical asymptotes at x = 3 and x = −1.
Horizontal Asymptotes (HAs)
Horizontal asymptotes describe the end behavior of the function as x→∞ or x→−∞. The asymptote is determined by the degrees of the polynomials in the numerator and denominator.
- Degree of numerator (n) vs. Degree of denominator (m):
- If n < m, the horizontal asymptote is y = 0.
- If n = m, the horizontal asymptote is y = leading coefficient of q(x)leading coefficient of p(x).
- If n > m, there is no horizontal asymptote, but there may be an oblique asymptote, which is found by polynomial division.
Example: Consider \( f(x) = \frac{3x^2 + 2x – 5}{2x^2 – x + 1} \).
- The degrees of both the numerator and denominator are 2, so the horizontal asymptote is 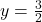\( y = \frac{3}{2} \), which is the ratio of the leading coefficients.
Holes
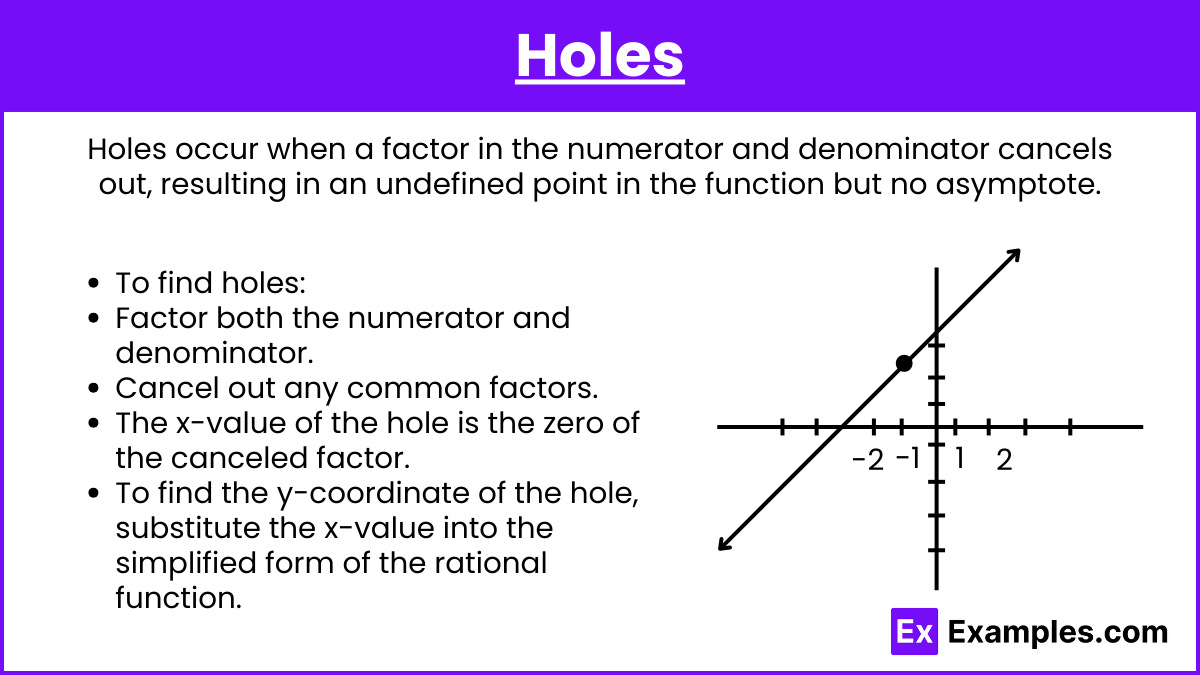
Holes occur when a factor in the numerator and denominator cancels out, resulting in an undefined point in the function but no asymptote.
- To find holes:
- Factor both the numerator and denominator.
- Cancel out any common factors.
- The x-value of the hole is the zero of the canceled factor.
- To find the y-coordinate of the hole, substitute the x-value into the simplified form of the rational function.
Example: Consider \( f(x) = \frac{(x – 1)(x + 2)}{(x – 1)(x + 3)} \)
- The factor (x−1) cancels out, leaving \( f(x) = \frac{x + 2}{x + 3} \).
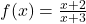- There is a hole at x = 1, and to find the y-value, substitute x=1 into the simplified function:
- \(f(1) = \frac{1 + 2}{1 + 3} = \frac{3}{4} \).
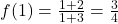- The hole occurs at \( (1, \frac{3}{4}) \).
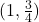Examples
Example 1
Function: \(f(x) = \frac{x + 2}{x – 4} \)
- Vertical Asymptote: The denominator is zero when x = 4, so there is a vertical asymptote at x = 4.
- Horizontal Asymptote: The degrees of the numerator and denominator are the same, both being 1. The horizontal asymptote is determined by the ratio of the leading coefficients. Since both are 1, the horizontal asymptote is y = 1.
- Holes: No factors cancel between the numerator and denominator, so there are no holes.
Example 2
Function: \(f(x) = \frac{x^2 – 9}{x^2 – 4x + 4} \)
- Vertical Asymptote: Factor the denominator: x2−4x+4 = (x−2)2. The vertical asymptote is at x = 2.
- Horizontal Asymptote: Since the degree of the numerator and denominator are the same, the horizontal asymptote is \(y = \frac{1}{1} = 1\).
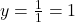- Holes: No common factors cancel between the numerator and denominator, so there are no holes.
Example 3
Function: \(f(x) = \frac{x^2 – 1}{x^2 – 1} \)
- Vertical Asymptote: Factor both the numerator and denominator: 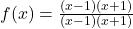\(f(x) = \frac{(x – 1)(x + 1)}{(x – 1)(x + 1)} \). Since both factors cancel, there are no vertical asymptotes.
- Horizontal Asymptote: Since the numerator and denominator are identical and cancel completely, the function is equal to 1 everywhere except for a hole.
- Holes: There is a hole at x = 1 and x = −1 where the factors cancel out.
Example 4
Function: \(f(x) = \frac{2x + 3}{x^2 – 4} \)
- Vertical Asymptote: Factor the denominator: 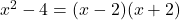\(x^2 – 4 = (x – 2)(x + 2) \). The vertical asymptotes are at x = 2 and x = −2.
- Horizontal Asymptote: The degree of the numerator (1) is less than the degree of the denominator (2), so the horizontal asymptote is y = 0.
- Holes: No common factors cancel between the numerator and denominator, so there are no holes.
Example 5
Function: \(f(x) = \frac{(x – 1)(x + 1)}{(x – 1)(x + 3)} \)
- Vertical Asymptote: The denominator equals zero at x = −3, so there is a vertical asymptote at x = −3.
- Horizontal Asymptote: The degrees of the numerator and denominator are equal, so the horizontal asymptote is y = 1, the ratio of the leading coefficients.
- Holes: The factor (x−1) cancels from both the numerator and denominator, creating a hole at x = 1. Substituting x = 1 into the simplified function 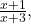\(\frac{x + 1}{x + 3},\), the hole is at (1,42)=(1,0.5).
Multiple Choice Questions
Question 1
For the function \( f(x) = \frac{(x+2)(x-1)}{(x-1)(x-3)} \), which of the following is true?
A. Vertical asymptotes at x = -2 and x = 3, and a hole at x = 1
B. Vertical asymptotes at x = 3, and a hole at x = 1
C. Vertical asymptotes at x = 1 and x = 3, no holes
D. No vertical asymptotes, and a hole at x = 1
Answer: B
Explanation:
- First, factor the numerator and denominator: \( f(x) = \frac{(x+2)(x-1)}{(x-1)(x-3)} \).
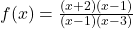- The factor (x−1) cancels out in both the numerator and denominator, creating a hole at x = 1.
- The remaining denominator, (x – 3), leads to a vertical asymptote at x = 3.
- Therefore, the correct answer is B.
Question 2:
Which of the following statements is correct for the rational function \( f(x) = \frac{3x^2 + 2x – 5}{x^2 + x – 6} \) ?
A. Horizontal asymptote at y = 3, vertical asymptotes at x = 2 and x = −3
B. Horizontal asymptote at y = 3, vertical asymptotes at x = -2 and x = 3
C. Horizontal asymptote at y = 3, vertical asymptotes at x = -2 and x = 3, and a hole at x = 2
D. Horizontal asymptote at y = 3, vertical asymptote at x = 3, and a hole at x = -2
Answer: D
Explanation:
- Factor the denominator: \( x^2 + x – 6 = (x – 2)(x + 3) \).
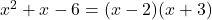- The numerator does not have any factors that cancel with the denominator, so there are vertical asymptotes at x = 2 and x = -3.
- For the horizontal asymptote, the degrees of the numerator and denominator are equal, so the horizontal asymptote is \( y = \frac{3}{1} = 3 \).
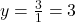- Since no factor cancels out, there are no holes. The correct answer is D.
Question 3
What is the horizontal asymptote of the function \( f(x) = \frac{2x^2 + 5x – 3}{4x^3 – x + 2} \) ?
A. y = 0
B. y = ∞
C. No horizontal asymptote
D. y = 2
Answer: A
Explanation:
- The degree of the numerator is 2, and the degree of the denominator is 3. Since the degree of the numerator is less than the degree of the denominator, the horizontal asymptote is y = 0, which indicates that the function approaches zero as x→∞ or x→−∞.
- Therefore, the correct answer is A.