Solve for x: 2x + 3 = 11
2
3
4
5


Lines are illustrations of the relationship between two points in a given plane. This means that the make and the direction are directly affected by the location of the two points. You can easily illustrate this relationship through linear equations and lines.
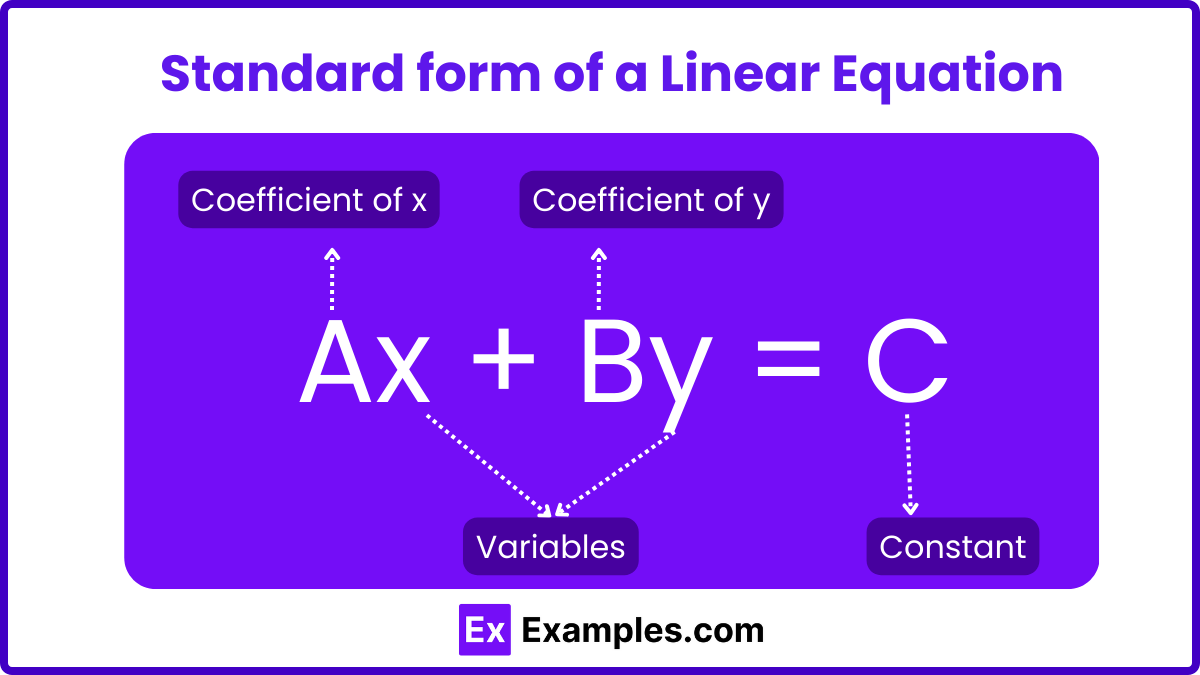
A linear equation is an algebraic equation in which each term is either a constant or the product of a constant and a single variable. Linear equations can be represented in various forms, but the most common is the standard form: ax+by=c
| Equations | Linear or Non-Linear |
|---|---|
| y = 8x – 10 | Linear |
| y = x² – 22 | Non-Linear, the power of the variable x is 2 |
| √y + x = 4 | Non-Linear, the power of the variable y is 1/2 |
| y + 8x – 1 = 0 | Linear |
| y² – x = 7 | Non-Linear, the power of the variable y is 2 |
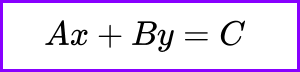
In this form, A, B, and C are constants. The equation describes a line in two-dimensional space, and neither variable is isolated on one side of the equation.

This is perhaps the most frequently used form when dealing with linear equations in basic algebra. Here, m represents the slope of the line, and b represents the y-intercept, which is the point where the line crosses the y-axis. This form makes it easy to graph the equation and to understand how changes in x affect y.
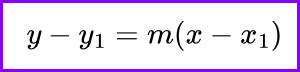
This form is useful when you know a point on the line (x₁,y₁) and the slope m. It’s particularly handy for writing the equation of a line when given a point and the slope without having to calculate the y-intercept.
The graph of a linear equation involving one variable, such as x, forms a vertical line that is parallel to the y-axis. Conversely, if the equation involves only the variable y, the graph will be a horizontal line parallel to the x-axis. On the other hand, the graph of a linear equation involving two variables, x and y, forms a straight line. This allows us to visually interpret the relationship between the variables. Let’s explore how to graph a linear equation with two variables through the following example:
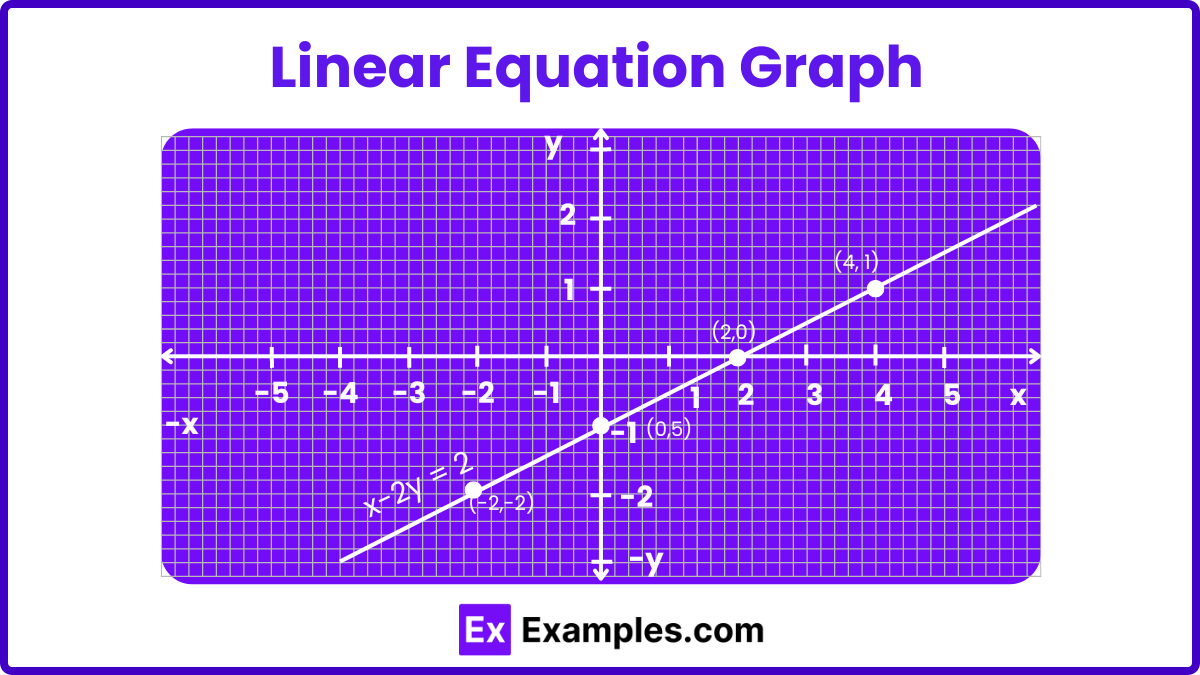
Example: Graphing the Linear Equation x−2y=2
To plot the graph of the linear equation in two variables, follow these steps:
Step 1: Identify the equation. The given equation is x−2y=2
Step 2: Convert the equation to slope-intercept form (y = mx + b). Rearrange x−2y=2 to express y in terms of x: y=(x/2)−1
This puts the equation in the form where m (slope) is 1/2 and b (y-intercept) is −1.
Step 3: Calculate coordinates by substituting different values of x.
Step 4: Plot these points and draw the line. List the coordinates and plot them on a Cartesian plane:
| x | 0 | 2 | 4 | -2 |
|---|---|---|---|---|
| y | -1 | 0 | 1 | -2 |
Connect these points with a straight line to visualize the relationship defined by the equation y=x/2−1. Each pair of (x, y) values satisfies the equation, illustrating the linear relationship between x and y.
Definition: A linear equation in one variable is an equation that can be written in the form ax+b=0, where aaa and bbb are constants and x is the variable. The goal is to find the value of x that makes the equation true.
Standard Form: ax+b=0
Steps to Solve:
Example: Solve 3x+5=11
Applications:
Definition: A linear equation in two variables is an equation that can be written in the form ax+by+c=0, where a, b, and c are constants, and x and y are variables. This type of equation represents a straight line when graphed on a coordinate plane.
Standard Form: ax+by+c=0
General Form: y=mx+b Where m is the slope and b is the y-intercept.
Methods to Solve:

Steps to Solve:
Methods to Solve:
Linear equations are equations that illustrate the proportional relationship between two variables and points. Simple linear equations are equations with a single variable, while there are linear equations with two variables, and even linear equations with three variables. All of which have their systems of linear equations and ways of solving said linear equations.
A can come in many different forms. The standard form of a linear equation with two variables is Ax + By = C where x is the X coordinate, y is the Y coordinate, and C is the constant number. One variable linear equation will come in the form of Ax + B = C.
Begin by writing down the equation in a physical note, or digital note-taking software. This will help you visualize the equation without needing to backread the question.
When you have finished writing down the equation, check whether the equation has one point or two points. You will be able to know this by the presence of X and Y coordinates in the equation. If the equation follows the Ax + By + C = 0 formats, it will require specific X and Y values that you can obtain from a different formula. Only use this how-to with equations that use the standard form of the linear equation or the standard one-variable linear equation.
When you have finished discerning the equation, you must simplify the equation to its simplest form. This means if there is a common denominator between the three variables, then you must divide them by said common denominator.
After you have simplified the equation, you must isolate and move one of the variables to the equals sign. The equation would either come in the form of x = C – B, Ax = C – By, or By = C – Ax.
After isolating one of the points, you must now substitute the isolated variable with specific points. For example, if 2x = 2 – Y is the linear equation, we can substitute the x value to be x = 0. The equation will then become 2(0) = 2 – Y, which will equal to Y = 2.
Repeat these steps until you have up to four sets of X and Y coordinates, note that each set will be a pair. Following the example above, the set of X and Y coordinates will be (0,2). Once you have four sets of these coordinates, graph the linear equation into the cartesian plane using these coordinates as your reference points. Afterward, you will connect all the reference points to create a straight line.
To solve linear equations, isolate the variable by performing inverse operations. Simplify the equation step-by-step, combining like terms and balancing both sides until the variable is isolated.
A linear equation has variables with an exponent of 1 and graphs as a straight line. It typically appears in the form ax+b=c Where a, b, and c are constants.
Linear equations represent relationships where the change between variables is constant. They are expressed in the form ax+by=c, producing straight-line graphs.
A linear equation is an algebraic equation with a constant rate of change between variables, represented as a straight line. Examples: y= 4x+2, 2x+3y = 6
A real-life example of a linear equation is calculating the total cost (C) of items given a fixed price per item (p) and quantity (q): C=pq.
A linear equation is like a simple rule that tells you how to get from one number to another using addition, subtraction, multiplication, or division. For example, if you have 2x+3=7, you find out what number makes it true.
Two linear equations form a system that can be solved together to find the values of variables that satisfy both equations. This can be done through methods like substitution or elimination.
Linear equations are equations and solutions that describe the direct relationship between two variables or values. These two values are often represented by the letters X and Y, which can be solved to obtain four points that will create a straight line.
Text prompt
Add Tone
10 Examples of Public speaking
20 Examples of Gas lighting
Solve for x: 2x + 3 = 11
2
3
4
5
Solve for y: 2y − 7 = 132
10
11
12
13
Find x: 4x + 9 = 3x + 15
5
6
7
8
Solve for y: 6y + 5 = 4y + 15
4
5
6
7
Solve for x: 9x − 2 = 4x + 13
1
2
3
4
Find x: 7x + 1 = 3x + 9
1
2
3
4
Solve for x: 6x + 2 = 3x + 11
3
4
5
6
Find y: 4y + 8 = 3y + 12
2
3
4
5
Solve for y: 8y − 3 = 3y + 17
1
2
3
4
Solve for y: 5y + 3 = 2y + 18
2
4
6
8
Before you leave, take our quick quiz to enhance your learning!

