Highest Common Factor

The world of mathematics with our in-depth guide on the Highest Common Factor (HCF). This fundamental concept, essential for both basic arithmetic and advanced algebra, paves the way for simplifying fractions, solving equations, and understanding number properties. Through practical examples, this guide elucidates the process of finding the HCF, enhancing your problem-solving skills and mathematical fluency. Perfect for students, educators, and math enthusiasts aiming to fortify their understanding of core mathematical principles.

What is Highest Common Factor (HCF) or Greatest Common Divisor (GCD)?

The Highest Common Factor (HCF), also known as the Greatest Common Divisor (GCD), is the largest number that divides two or more numbers without leaving a remainder. It’s a key concept in mathematics that helps in simplifying fractions, comparing ratios, and solving various problems involving whole numbers. In simple terms, if you have a set of numbers, the HCF is the biggest number that all of these numbers can be divided by evenly. This concept is not only fundamental in arithmetic but also plays a crucial role in algebra and number theory, making it an essential tool for students and mathematicians alike.

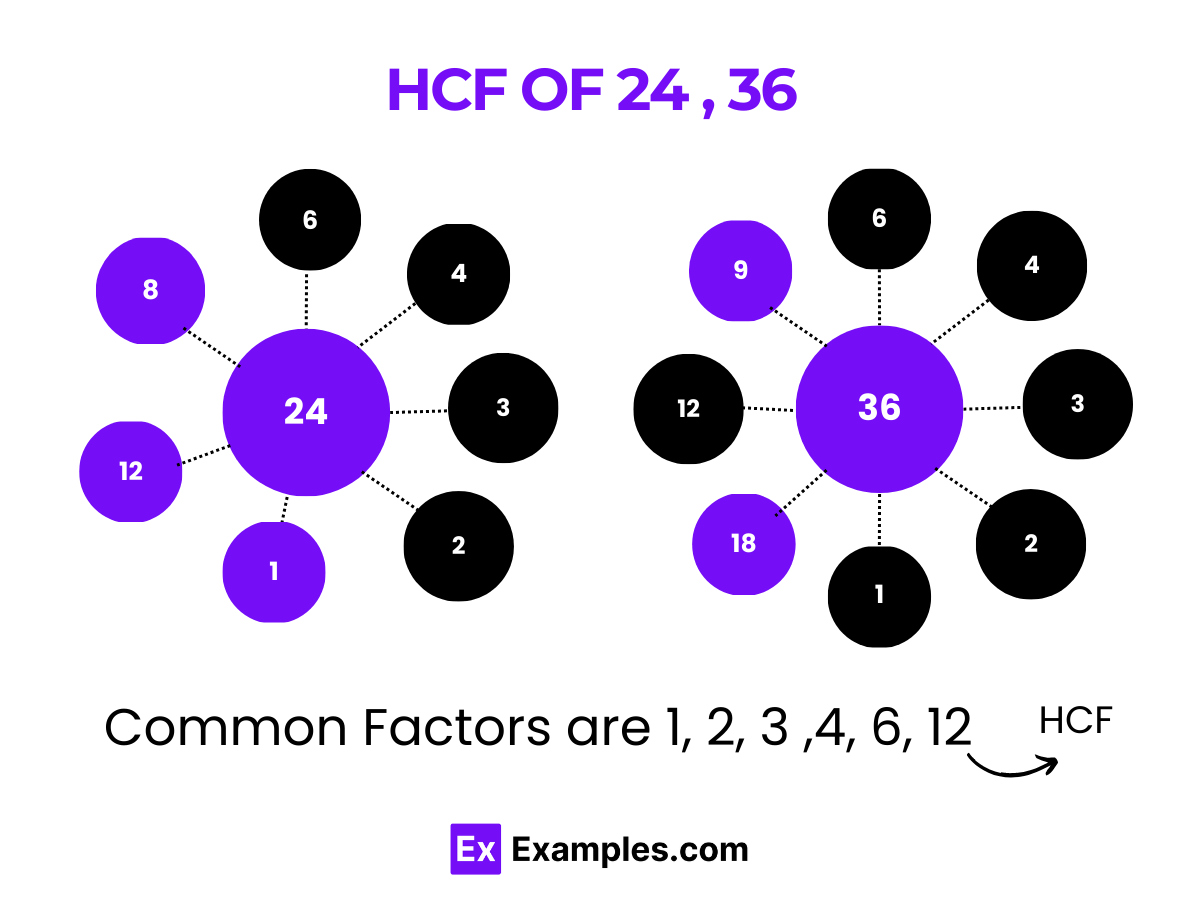Let’s find the HCF of 24 and 36.

1.  List the factors of each number:
   • Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24
   • Factors of 36: 1, 2, 3, 4, 6, 9, 12, 18, 36
2. Identify the common factors:
   • Common factors: 1, 2, 3, 4, 6, 12
3. Choose the highest common factor:
   • Highest Common Factor (HCF): 12.

How to Find  Highest Common Factor (HCF)

Discover the essential methods to calculate the Highest Common Factor (HCF), a fundamental concept in mathematics that simplifies numbers and expressions. This guide will walk you through different techniques, accompanied by clear examples and step-by-step calculations to enhance your understanding and skills.

1. Find  HCF By Prime Factorization

Prime factorization involves breaking down each number into its prime factors and then identifying the common prime factors to find the HCF.

Let’s find the HCF of 48 and 60.

1. Prime Factorization:
   • 48 = 2⁴×3
   • 60 = 2×2×3×5
2. Identify Common Prime Factors:
   • Common factors: 2×2×3
3. Calculate HCF:
   • HCF = 2×2×3=12

HCF of 48 and 60 is 12.

2. Find  HCF By Division Method

The division method, also known as the Euclidean algorithm, is a systematic approach to finding the HCF by dividing the larger number by the smaller number until the remainder is zero.

Let’s Find the HCF of 105 and 45.

1. Divide the Larger Number by the Smaller Number:
   • Step 1: $105÷45=2$ remainder 15
   • Step 2: $45÷15=3$ remainder 0
2. Last Divisor as HCF:
   • The last non-zero remainder is 15.

HCF of 105 and 45 is 15.

Properties of the Highest Common Factor (HCF)

Grasping the properties of the Highest Common Factor (HCF) can significantly enhance your mathematical problem-solving skills. This guide delves into the fundamental characteristics of HCF, providing a clearer understanding of its applications and utility in various mathematical contexts.

1. HCF is Always a Positive Integer

The Highest Common Factor, by definition, is a positive integer. It represents the largest number that can divide two or more integers without leaving a remainder. This property is essential for simplifying fractions and finding equivalent ratios, making HCF a cornerstone in arithmetic and algebra.

2. HCF of Prime Numbers is 1

When dealing with prime numbers, which are numbers greater than 1 that have no divisors other than 1 and themselves, the HCF is always 1. This is because prime numbers do not share any common factors other than 1, highlighting the fundamental aspect of prime numbers in number theory.

3. HCF and LCM Relationship

One of the most intriguing properties of HCF is its relationship with the Least Common Multiple (LCM). For any two numbers, the product of their HCF and LCM is equal to the product of the numbers themselves. This relationship is pivotal in solving problems that involve both HCF and LCM, providing a dual approach to understanding number relationships.

4. HCF is Not Greater Than Any of the Numbers

The Highest Common Factor cannot be greater than the smallest number among the ones being considered. This property is logical since the HCF is a factor that all the numbers share, and a factor is always less than or equal to the number itself.

5. HCF Can Be Used to Simplify Fractions

One of the practical applications of HCF is in the simplification of fractions. By finding the HCF of the numerator and denominator, you can reduce fractions to their simplest form. This property is particularly useful in fraction addition, subtraction, multiplication, and division, ensuring the results are presented in the most simplified manner.

Relation between LCM and HCF

Dive into the intricate world of mathematics as we unravel the fundamental relationship between two key concepts: the Least Common Multiple (LCM) and the Highest Common Factor (HCF). This relationship is not merely a mathematical curiosity; it’s a powerful tool that bridges the gap between understanding individual numbers and how they interact within the mathematical universe.

At the core of the relationship between LCM and HCF is a simple, yet profound equation:

HCF×LCM=Product of the two numbers

This equation signifies a deep connection between the LCM and HCF of any two numbers, asserting that their product is always equal to the product of the numbers themselves. This foundational principle applies universally to all pairs of integers and is instrumental in solving a wide array of mathematical problems.

Let’s solidify this concept with a concrete example, using the numbers 20 and 30 to explore their LCM and HCF.

1. Calculating HCF:
   • Begin by determining the HCF of 20 and 30, the largest number that divides both without leaving a remainder.
   • Through prime factorization or listing factors, we find:
     • HCF(20,30)=10
2. Calculating LCM:
   • The LCM is the smallest common multiple that 20 and 30 can both divide into evenly.
   • Utilizing prime factorization or the division method, we ascertain:
     • LCM(20,30)=60
3. Applying the Relationship:
   • Verify the relationship by multiplying the HCF and LCM:
     • HCF×LCM=10×60=600
   • Confirm the equation by multiplying the original numbers:
     • 20×30=600

The calculation not only validates the relationship but also highlights the seamless interplay between the HCF and LCM, demonstrating that the product of 10 (HCF) and 60 (LCM) of the numbers 20 and 30 equals the product of 20 and 30 themselves (600). This example serves as a testament to the reliability and applicability of the HCF-LCM relationship across different numerical scenarios.

HCF of Three Numbers

Finding the Highest Common Factor (HCF) of three numbers involves identifying the largest number that divides all three numbers without any remainder. This process is crucial for simplifying fractions and solving problems that involve multiple numbers.

 Find the HCF of 24, 36, and 48

1. Prime Factorization:
   • 24 = 2×2×2×3
   • 36 = $\times 3$
   • 48 = 2⁴×3
2. Identify Common Prime Factors:
   • • Common factors: 2²×3
3. Calculate HCF:
   • HCF =2²×3=12

The HCF of 24, 36, and 48 is 12, which is the largest number that divides all three numbers evenly.

HCF of Four Numbers

When dealing with four numbers, the process to find the HCF remains consistent with finding the greatest common divisor that evenly divides all four numbers.

 Find the HCF of 16, 32, 48, and 64

1. Prime Factorization:
   • 16 = 2⁴
   • 32 = 2⁵
   • 48 = 2⁴×3
   • 64 = 2⁶
2. Identify Common Prime Factors:
   • Common factors: 2⁴
3. Calculate HCF:
   • HCF = 2⁴$=16$

The HCF of 16, 32, 48, and 64 is 16, showcasing the largest number that all four numbers can be divided by without a remainder.

HCF of Prime Numbers

Prime numbers are numbers that have only two distinct positive divisors: 1 and the number itself. The HCF of any two prime numbers is always 1, as they do not share any other divisors.

Find the HCF of 13, 17, and 19

1. Prime Numbers:
   • 13, 17, and 19 are all prime.
2. Identify Common Factors:
   • The only common factor among prime numbers is 1.
3. Calculate HCF:
   • HCF = 1

The HCF of any set of prime numbers, such as 13, 17, and 19, is always 1, reflecting the unique property of prime numbers having no common divisors other than 1.

In conclusion, understanding the Highest Common Factor (HCF) is fundamental in mathematics, offering essential insights into number theory and algebra. It simplifies expressions, aids in solving equations, and enhances problem-solving skills. Mastering HCF calculation methods enriches mathematical proficiency, making it a pivotal concept for students, educators, and math enthusiasts seeking to deepen their comprehension of mathematical relationships and operations.