Least Common Multiple (LCM)

The fascinating realm of mathematics with our comprehensive guide on the Least Common Multiple (LCM). This essential concept, pivotal for seamless calculations in arithmetic, algebra, and beyond, serves as the cornerstone for solving diverse problems involving fractions, equations, and number theory. Unravel the mysteries of LCM through illustrative examples, unlocking efficient problem-solving techniques. Embrace this journey to elevate your mathematical proficiency and navigate through numerical challenges with ease.

What is the Least Common Multiple (LCM)?

The Least Common Multiple (LCM) is the smallest number that is a multiple of two or more numbers. It’s the minimum shared value that all given numbers divide into without leaving a remainder.

Consider the numbers 4 and 5. To find the LCM of 4 and 5, we list their multiples:

• Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, …
• Multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40, …

Looking at these lists, the smallest number that appears in both lists is 20. Therefore, 20 is the Least Common Multiple of 4 and 5. This means 20 is the smallest number that both 4 and 5 can divide into without leaving any remainder.

How to Find  Least Common Multiple (LCM)

The Least Common Multiple (LCM) of two or more numbers is the smallest number that is a multiple of all these numbers. It’s a fundamental concept in mathematics, particularly useful in solving problems involving fractions, algebra, and number theory. Understanding how to find the LCM can simplify calculations and help in comparing or combining different quantities.

Before diving into methods for finding the LCM, it’s essential to grasp its significance. The LCM is used to find a common denominator in fractions, which simplifies adding, subtracting, and comparing them. It’s also crucial in solving equations with multiple terms and in real-life situations like scheduling events that have different repeating cycles.

They are three ways to find Least Common Multiple(LCM) :

• Prime Factorization Method
• Listing Multiples Method
• Division Method

1. Prime Factorization Method

1. Break Down Each Number: Decompose each number into its prime factors.
2. Identify Common and Unique Factors: For each number, list out all prime factors, considering the highest power of each prime that appears in any of the numbers.
3. Multiply the Highest Powers of All Prime Factors: The product of these factors will give you the LCM.

To find the LCM of 12 and 18 using prime factorization:

• Prime factors of 12: 2×2×3
• Prime factors of 18: 2×3×3
• LCM: $=36$

2. Listing Multiples Method

1. List Multiples of Each Number: Start listing multiples of each number until you find the first common multiple.
2. Identify the Least Common Multiple: The first common multiple you encounter is the LCM.

For numbers 4 and 5, the multiples are:

• 4: 4, 8, 12, 16, 20, 24…
• 5: 5, 10, 15, 20, 25…

The LCM is 20, the first common multiple.

3. Division Method

1. Divide by Common Prime Numbers: Begin with the smallest prime number (usually 2) and divide the given numbers if possible. Write the quotient below each number.
2. Repeat Until No More Division is Possible: Continue dividing by prime numbers (2, 3, 5, etc.) until no numbers can be evenly divided.
3. Multiply All Divisors and Remaining Numbers: The product of all the divisors and the remaining numbers at the bottom is the LCM.

 

Finding the LCM of 14 and 20:

• Divide by 2: Quotients are 7 (for 14) and 10 (for 20).
• Divide by 2 again: Quotients are 7 and 5.
• Multiply all divisors and remaining numbers: 2×2×7×5=140.

LCM Formula

The Least Common Multiple (LCM) of two numbers, $a$ and $b$, can be found using the formula:

LCM(a, b)=∣a× b∣÷ GCD (a, b)​

Here, ∣a× b∣ represents the absolute value of the product of $a$ and $b$, and GCD(a, b) is the Greatest Common Divisor of $a$ and $b$. This formula efficiently combines multiplication and division, leveraging the relationship between the LCM and GCD to find the smallest multiple common to both numbers.

let’s solve for the LCM of 15 and 20:

1. First, find the Greatest Common Divisor (GCD) of 15 and 20. The GCD of 15 and 20 is 5.
2. Then, multiply the numbers together: 15×20=300
3. Finally, divide the product by the GCD: 300÷ 5= 60

Therefore, the Least Common Multiple (LCM) of 15 and 20 is 60. ​

Properties of Least Common Multiple (LCM)

The Least Common Multiple (LCM) is a fundamental concept in mathematics that plays a pivotal role in various computational processes, including solving equations, simplifying fractions, and analyzing number sets. Understanding the properties of LCM not only enhances one’s mathematical prowess but also lays the groundwork for advanced mathematical applications.

Property	Description	Mathematical Expression
Commutative Property	The order of numbers does not change the LCM.	LCM(a, b)=LCM(b ,a)
Associative Property	Grouping of numbers does not affect the LCM.	$\text{LCM}(a,\text{LCM}(b,c))=\text{LCM}(\text{LCM}(a,b),c)$
Distributive Property over GCD	The product of LCM and GCD of two numbers equals the absolute product of those numbers.	LCM(a, b)×GCD(a, b)=∣a× b∣
LCM of Coprime Numbers	The LCM of coprime numbers (with a GCD of 1) is the product of those numbers.	If GCD(a, b)=1, then LCM(a ,b)=∣a× b∣
LCM in Relation to Multiples	The LCM is always a multiple of the numbers involved and is equal to or greater than the largest number.	$\text{LCM}(a,b)\ge \max (a,b)$

Least Common Multiple (LCM) of Two Numbers

The Least Common Multiple (LCM) of two numbers is a foundational concept in mathematics that finds extensive application across various domains, from solving fraction-based problems to scheduling and planning. It represents the smallest number that is a multiple of both numbers, facilitating arithmetic operations and problem-solving with ease and efficiency. Grasping the LCM concept is crucial for students, educators, and professionals who deal with mathematical computations regularly.

To compute the LCM of two numbers, several methods can be employed, each suited to different situations and complexity levels. The most common approaches include the prime factorization method, where numbers are broken down into their prime components, and the division method, which systematically reduces numbers using common divisors. Choosing the right method depends on the numbers at hand and the solver’s comfort with mathematical operations.

To elucidate the concept, let’s consider an example of finding the LCM of 12 and 15 using the prime factorization method:

1. Prime Factorization:
   • Break down each number into its prime factors.
     • 12 = 2×2×3
     • 15 = 3×5
2. Identify Unique Factors:
   • List all prime factors found in both numbers, without repetition, and for each prime, use the highest power found in either number.
     • The prime factors are 2, 3, and 5.
     • The highest powers are 2² (from 12) and 3 and 5 (from 15).
3. Calculate the LCM:
   • Multiply these factors together to find the LCM.
     • LCM = 2²×3×5=4×3×5=60

Therefore, the LCM of 12 and 15 is 60, meaning 60 is the smallest number into which both 12 and 15 can evenly divide.

Least Common Multiple (LCM) of Three Numbers

The Least Common Multiple (LCM) extends beyond pairs of numbers, applying to sets of three or more, serving as a crucial tool in mathematics for simplifying complex problems. The LCM of three numbers is the smallest number that all three numbers divide into evenly, facilitating operations involving fractions, scheduling, and more. Understanding how to compute the LCM for three numbers is vital for anyone looking to deepen their mathematical skills and apply them in various contexts.

Calculating the LCM of three numbers can be approached in multiple ways, with the prime factorization and division methods being the most common. The prime factorization involves breaking each number into its prime components and combining them to find the LCM, while the division method systematically reduces the numbers using common divisors. The choice of method often depends on the specific numbers and the solver’s preference for mathematical techniques.

 

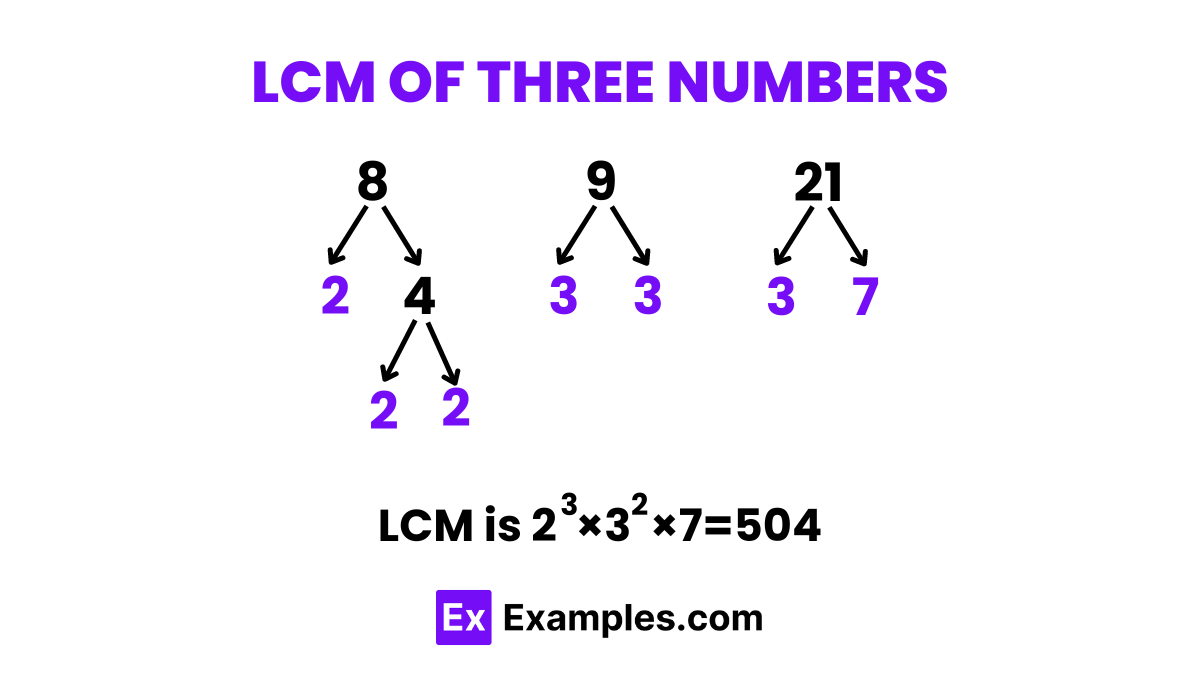
Let’s illustrate the process with an example, calculating the LCM of 8, 9, and 21 using the prime factorization method:

1. Prime Factorization:
   • Decompose each number into prime factors.
     • 8 = 2³
     • 9 = 3²
     • 21 = 3×7
2. Combine Unique Factors:
   • Identify all unique prime factors from the three numbers, taking the highest power of each prime that appears.
     • The prime factors are 2, 3, and 7.
     • The highest powers are 2³(from 8), 3² (from 9), and 7 (from 21).
3. Compute the LCM:
   • Multiply the highest powers of these prime factors to get the LCM.
     • LCM = 2³×3²×7=8×9×7=504

Thus, the LCM of 8, 9, and 21 is 504, the smallest number that all three integers divide into without leaving a remainder.

Relationship Between LCM and HCF

The mathematical concepts of Least Common Multiple (LCM) and Highest Common Factor (HCF), also known as Greatest Common Divisor (GCD), are intertwined in a fascinating relationship that is fundamental to number theory and arithmetic. Understanding the connection between LCM and HCF is crucial for solving various mathematical problems efficiently, from simplifying fractions to determining ratios and solving equations.

LCM and HCF are two sides of the same coin in mathematics, each serving a unique purpose but also complementing each other. While LCM determines the smallest common multiple shared by two or more numbers, HCF finds the largest factor that divides those numbers without a remainder. The relationship between them is not just theoretical but practical, aiding in problem-solving and mathematical reasoning.

To clearly understand the relationship between LCM and HCF, let’s explore their connection through a table that outlines the key aspects of their interrelation:

Aspect	LCM	HCF
Definition	The smallest number that is a multiple of two or more numbers.	The largest number that divides two or more numbers without leaving a remainder.
Computation Method	Through prime factorization or the division method.	By listing factors or using the Euclidean algorithm.
Usage	To find a common multiple for operations like adding fractions.	To simplify fractions or find common divisors.
Relation Formula	LCM(a, b) = a × b / GCF(a, b)	GCF(a, b) = a × b / LCM(a, b)
Example	LCM of 12 and 15 is 60.	HCF of 12 and 15 is 3.

This table encapsulates the core aspects of LCM and HCF, illustrating their distinct roles and the mathematical formula that binds them together. It’s evident that while they serve different purposes, the relationship$\text{LCM}(a,b)\times \text{HCF}(a,b)=|a\times b|$ showcases a direct and profound connection, emphasizing the balance and symmetry inherent in mathematics.

Least Common Multiple Chart

The combined LCM chart for pairs and sets of numbers serves as a versatile tool, offering a snapshot of the Least Common Multiple for various groupings. It simplifies the process of finding the smallest number that is a multiple of two or more integers, aiding in mathematical calculations across different contexts. From simplifying fractions to solving complex problems that require a common denominator, this chart is an essential reference.

Numbers	LCM
4, 5	20
6, 8	24
7, 14	14
9, 12	36
10, 15	30
3, 4, 5	60
18, 24	72
20, 25	100
11, 22	22
2, 7, 8	56
13, 26	26
6, 9, 12	36
16, 20	80
10, 20, 25	100
14, 15, 21	210

1. Find LCM of 6 and 8?

1. Prime Factorization:
   • 6 = 2×3
   • 8 = 2×2×2
2. Combine Unique Factors with Highest Powers:
   • Combine  2³ (from 8) and 3 (from 6).
3. Calculate LCM:
   • LCM = 8×3=24

The LCM of 6 and 8 is 24.

2. Find LCM of 14 and 20

1. Prime Factorization:
   • 14 = 2×7
   • 20 = 2×2×5
2. Combine Unique Factors with Highest Powers:
   • Combine 4(from 20), 5 (from 20), and 7 (from 14).
3. Calculate LCM:
   • LCM = =4×5×7=140

The LCM of 14 and 20 is 140.

 3. Find LCM of 18, 24, and 30

1. Prime Factorization:
   • 18 = 2×3²
   • 24 = 2³×3
   • 30 = 2×3×5
2. Combine Unique Factors with Highest Powers:
   • Combine 2³ (from 24), 3² (from 18), and 5 (from 30).
3. Calculate LCM:
   • LCM = 8×9×5=360

The LCM of 18, 24, and 30 is 360.

In conclusion, understanding the Least Common Multiple (LCM) is essential for simplifying mathematical problems and finding common denominators. Through methods like prime factorization, calculating the LCM becomes straightforward, aiding in diverse applications from fraction operations to scheduling tasks. Mastering LCM calculations not only enhances mathematical proficiency but also equips learners with critical problem-solving skills.