Trigonometry Values , Examples, Pdf
Trigonometry is a fascinating branch of mathematics that deals with the relationships between the angles and sides of triangles. Central to this are trigonometry formulas, which allow us to solve problems in engineering, physics, and even astronomy. These formulas, including sine, cosine, and tangent, help us understand and apply the properties of right triangles. By mastering trigonometry formulas, students and professionals can enhance their analytical skills and solve complex spatial problems. Overall, trigonometry values are not just theoretical; they have practical applications in various scientific and real-world contexts.
What are Trigonometry Values?
Trigonometry values refer to the ratios of the sides of a right triangle relative to one of its acute angles. These values are fundamental in trigonometry, a branch of mathematics that deals with the relationships between angles and sides of triangles.
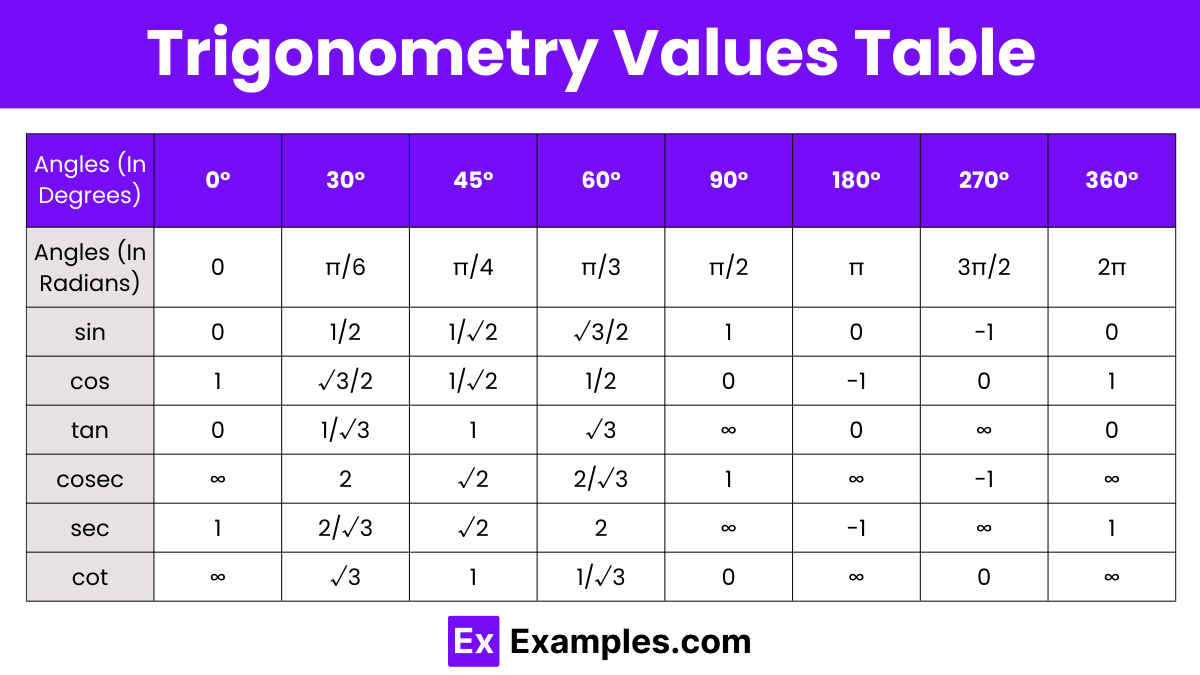
Trigonometry Values Table
Let’s explore the trigonometric values for angles 0°, 30°, 45°, 60°, and 90°, covering the functions sine (sin), cosine (cos), tangent (tan), cotangent (cot), secant (sec), and cosecant (csc). We’ll use the context of a right triangle to understand how these values are calculated and their significance. This exploration will provide a practical understanding of how each trigonometric function relates to specific angles in a triangle, enhancing our grasp of fundamental trigonometric concepts. To assist with this, you can download a Trigonometry formula table that includes all these values for quick reference.
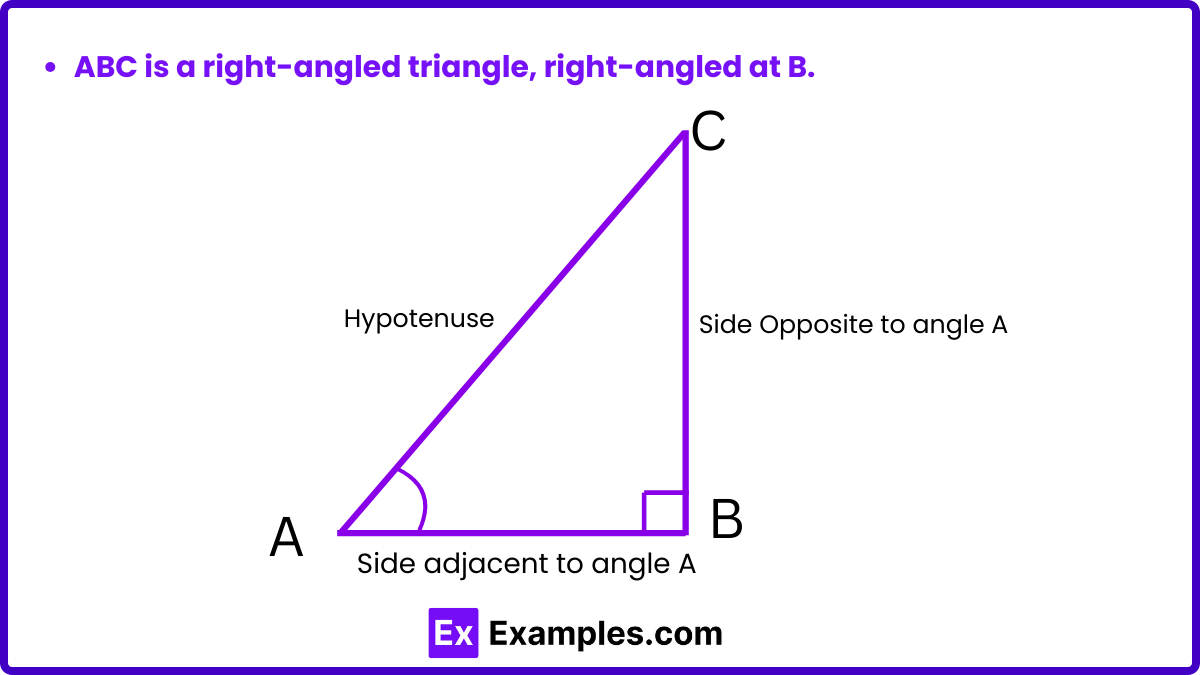
Consider the right-angled triangle ABC, where angle B is a right angle. In this triangle, the hypotenuse is AC. The side AB, adjacent to angle θ, is referred to as the adjacent side, while the side BC, opposite angle θ, is known as the perpendicular side
Trigonometry values are based on three major trigonometric ratios, Sine, Cosine, and Tangent.
- sin θ = Perpendicular/Hypotenuse=BC/AC
- cos θ = Base/Hypotenuse=AB/AC
- tan θ = Perpendicular/Base=BC/AB
Similarly, we can define the reciprocal trigonometric properties for the ratios secant (sec), cosecant (csc), and cotangent (cot).
- sec θ = Hypotenuse/Base=AC/AB
- cosec θ = Hypotenuse/Perpendicular=AC/AB
- cot θ = Base/Perpendicular=AB/BC
- Sec θ . Cos θ =1
- Cosec θ . Sin θ =1
- Cot θ . Tan θ =1
Trigonometry Ratios Formula
- Tan θ = sin θ/cos θ
- Cot θ = cos θ/sin θ
- Sin θ = 1/cosec θ
- Cos θ = sin θ/tan θ = 1/sec θ
- Sec θ = tan θ/sin θ = 1/cos θ
- Cosec θ = 1/sin θ
Also,
- Sin (90°-θ) = Cos θ
- Cos (90°-θ) = Sin θ
- Tan (90°-θ) = Cot θ
- Cot (90°-θ) = Tan θ
- Sec (90°-θ) = Cosec θ
- Cosec (90°-θ) = Sec θ
What are the values of trigonometry?
Trigonometry values are ratios of the sides of a right triangle in relation to one of its acute angles, specifically through sine, cosine, and tangent functions.
How to find trigonometric value?
To find trigonometric values, use the sine, cosine, or tangent functions based on the angle and the triangle side lengths: opposite, adjacent, or hypotenuse.
What are the 7 formulas of trigonometry?
The seven main trigonometry formulas include the sine, cosine, tangent, and their reciprocals (cosecant, secant, cotangent), plus the Pythagorean identity.
What are the 6 basic trigonometry?
The six basic trigonometric functions are sine, cosine, tangent, cosecant, secant, and cotangent, which relate angles to side ratios in a right triangle.
How to do trigonometry for beginners?
Beginners should start by understanding right triangles and the definitions of sine, cosine, and tangent, followed by practicing basic problems.
How to memorize six trigonometric ratios?
To memorize the six trigonometric ratios, associate each with its function and reciprocal (sin, cos, tan, csc, sec, cot) and practice regularly using mnemonic devices.
What are all six trig identities?
The six fundamental trig identities include the Pythagorean identity, quotient identities, and reciprocal identities for sine, cosine, and tangent.
How to do trigonometry formula?
Apply trigonometry formulas by identifying the correct function to use based on the given angle and triangle sides, and use identities to simplify expressions.
What is a simple trick to remember trigonometric ratios?
A simple trick to remember trigonometric ratios is to use the mnemonic “SOH CAH TOA” which stands for Sine = Opposite/Hypotenuse, Cosine = Adjacent/Hypotenuse, Tangent = Opposite/Adjacent.
How to learn easily trigonometry table?
Learn the trigonometry table by starting with key angles (0°, 30°, 45°, 60°, 90°) and their sine, cosine, and tangent values, using visual aids and repetition.
What is the trick to solve trigonometry?
A useful trick for solving trigonometry is to understand the unit circle, where each point represents an angle’s cosine and sine, and to use identity formulas.
How to find trigonometric ratios?
Find trigonometric ratios by identifying the correct sides of a right triangle related to a specific angle and applying the sine, cosine, or tangent functions.



