What is the value of logāā 1?
0
1
-1
2
of 10
Value of Log 1 to 10 – Values, Table, Chart in PDF
Value of Log 1 to 10 – Values, Table, Chart in PDF
Logarithms are mathematical functions that help to solve equations involving exponential growth or decay. The logarithm of a number is the exponent to which the base must be raised to produce that number. For instance, the logarithm of 1000 to the base 10 is 3, because 10Ā³ = 10001. In other words, logarithms can be considered as the inverse operations of exponentiation.
Logarithms are essential in various fields including science, engineering, and economics. They are used for simplifying complex calculations, especially when dealing with very large or very small numbers. Understanding the logarithms of basic numbers like 1 to 10 lays a strong foundation for more advanced mathematical concepts and applications.
Download Value of Log 1 to 10 in PDF
Value of Log 1 to 10
Download Value of Log 1 to 10 in PDF
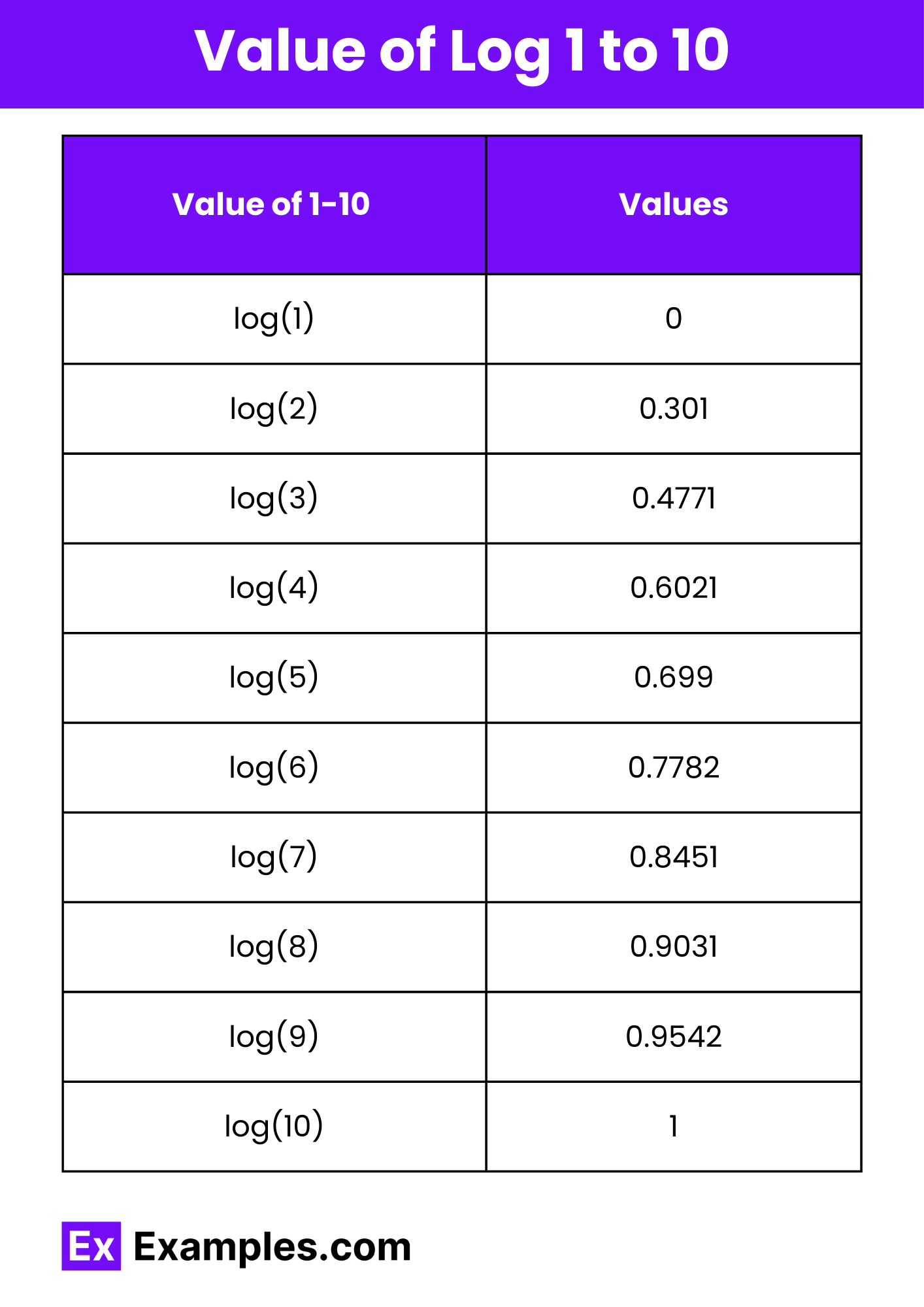
Here is the table for the logarithmic values (base 10) of numbers from 1 to 10:
| Value of Log 1 to 10 | Values | In Words |
|---|---|---|
| log(1) | 0 | Zero |
| log(2) | 0.3010 | Zero point three zero one zero |
| log(3) | 0.4771 | Zero point four seven seven one |
| log(4) | 0.6021 | Zero point six zero two one |
| log(5) | 0.6990 | Zero point six nine nine zero |
| log(6) | 0.7782 | Zero point seven seven eight two |
| log(7) | 0.8451 | Zero point eight four five one |
| log(8) | 0.9031 | Zero point nine zero three one |
| log(9) | 0.9542 | Zero point nine five four two |
| log(10) | 1 | One |
The value of logarithms for numbers 1 to 10 in base 10 (common logarithms) ranges from 0 to 1. Specifically, log(1) = 0, log(2) ā 0.301, log(3) ā 0.477, log(4) ā 0.602, log(5) ā 0.699, log(6) ā 0.778, log(7) ā 0.845, log(8) ā 0.903, log(9) ā 0.954, and log(10) = 1. These values represent the exponents to which the base 10 must be raised to obtain the respective numbers, illustrating the logarithmic scale’s ability to transform multiplicative relationships into additive ones, which is particularly useful in various scientific and mathematical applications.
Share :
Practice Test
What is the value of logāā 10?
0
1
10
-1
of 10
Find the value of logāā 100.
1
2
10
100
of 10
What is the value of logāā 1000?
2
3
10
100
of 10
What is the value of logāā 0.1?
0
1
-1
2
of 10
Find the value of logāā 0.01.
-1
-2
1
2
of 10
What is the value of logāā 10000?
4
3
2
1
of 10
What is the value of logā 8?
1
2
3
4
of 10
Find the value of logā 16.
2
3
4
5
of 10
What is the value of logāā 50?
1.7
2
1.5
10
of 10