Value of Log 1 to 50
Value of Log 1 to 50
Logarithms are mathematical functions that help to solve equations involving exponential growth or decay. The logarithm of a number is the exponent to which the base must be raised to produce that number. For instance, the logarithm of 1000 to the base 10 is 3, because 10³ = 10001. In other words, logarithms can be considered as the inverse operations of exponentiation.
This introduction will focus on the common logarithms of numbers from 1 to 50. Understanding these values can help simplify complex calculations, solve exponential equations, and analyze growth patterns. The logarithm values presented here are typically approximated to four decimal places for practical use.
Download Value of Log 1 to 50 in PDF
Value of Log 1 to 50
Download Value of Log 1 to 50 in PDF
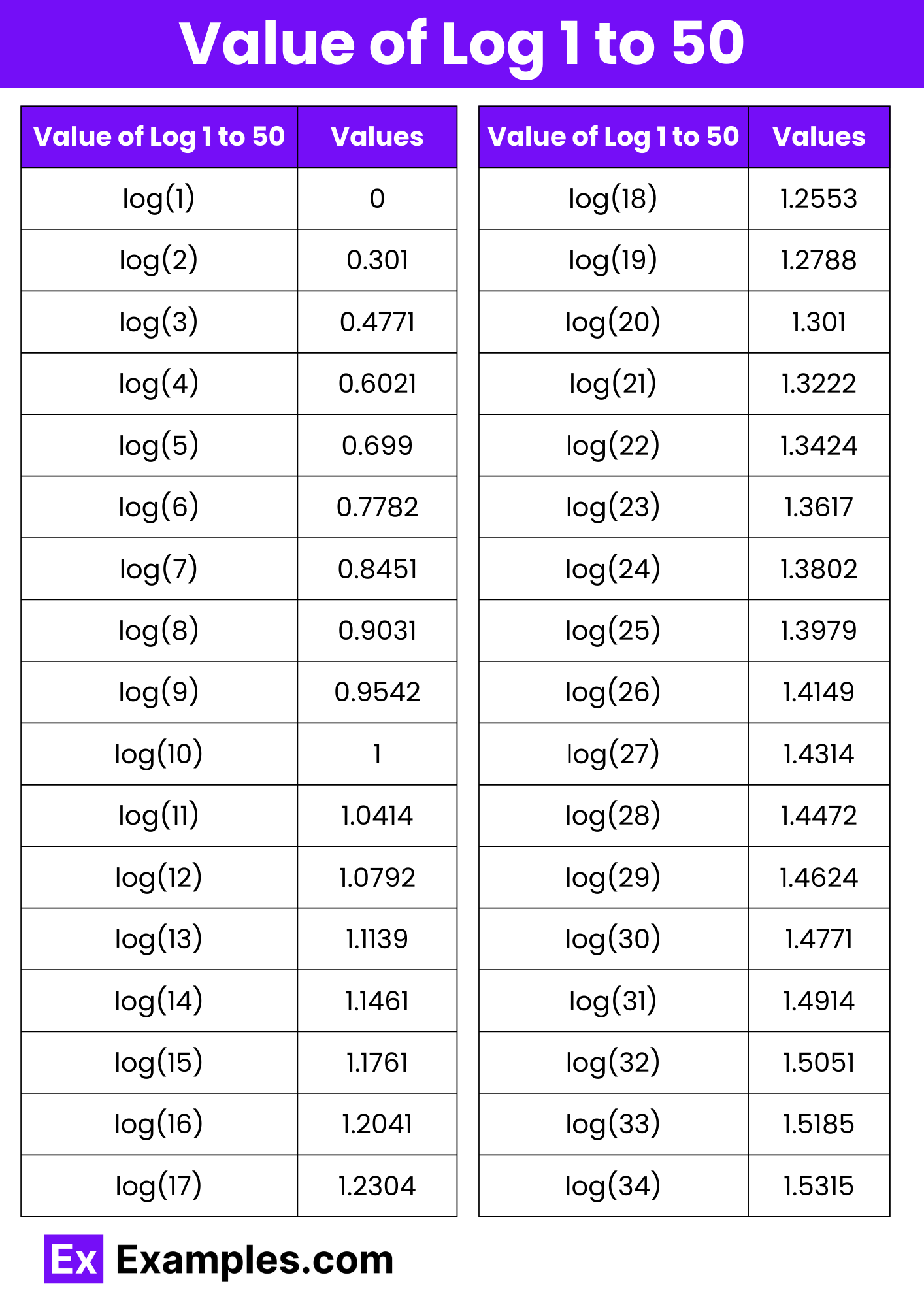
| Value of Log 1 to 50 | Values | In Words |
|---|---|---|
| log(1) | 0.0000 | Zero point zero zero zero zero |
| log(2) | 0.3010 | Zero point three zero one zero |
| log(3) | 0.4771 | Zero point four seven seven one |
| log(4) | 0.6021 | Zero point six zero two one |
| log(5) | 0.6990 | Zero point six nine nine zero |
| log(6) | 0.7782 | Zero point seven seven eight two |
| log(7) | 0.8451 | Zero point eight four five one |
| log(8) | 0.9031 | Zero point nine zero three one |
| log(9) | 0.9542 | Zero point nine five four two |
| log(10) | 1.0000 | One point zero zero zero zero |
| log(11) | 1.0414 | One point zero four one four |
| log(12) | 1.0792 | One point zero seven nine two |
| log(13) | 1.1139 | One point one one three nine |
| log(14) | 1.1461 | One point one four six one |
| log(15) | 1.1761 | One point one seven six one |
| log(16) | 1.2041 | One point two zero four one |
| log(17) | 1.2304 | One point two three zero four |
| log(18) | 1.2553 | One point two five five three |
| log(19) | 1.2788 | One point two seven eight eight |
| log(20) | 1.3010 | One point three zero one zero |
| log(21) | 1.3222 | One point three two two two |
| log(22) | 1.3424 | One point three four two four |
| log(23) | 1.3617 | One point three six one seven |
| log(24) | 1.3802 | One point three eight zero two |
| log(25) | 1.3979 | One point three nine seven nine |
| log(26) | 1.4149 | One point four one four nine |
| log(27) | 1.4314 | One point four three one four |
| log(28) | 1.4472 | One point four four seven two |
| log(29) | 1.4624 | One point four six two four |
| log(30) | 1.4771 | One point four seven seven one |
| log(31) | 1.4914 | One point four nine one four |
| log(32) | 1.5051 | One point five zero five one |
| log(33) | 1.5185 | One point five one eight five |
| log(34) | 1.5315 | One point five three one five |
| log(35) | 1.5441 | One point five four four one |
| log(36) | 1.5563 | One point five five six three |
| log(37) | 1.5682 | One point five six eight two |
| log(38) | 1.5798 | One point five seven nine eight |
| log(39) | 1.5911 | One point five nine one one |
| log(40) | 1.6021 | One point six zero two one |
| log(41) | 1.6128 | One point six one two eight |
| log(42) | 1.6232 | One point six two three two |
| log(43) | 1.6335 | One point six three three five |
| log(44) | 1.6435 | One point six four three five |
| log(45) | 1.6532 | One point six five three two |
| log(46) | 1.6628 | One point six six two eight |
| log(47) | 1.6721 | One point six seven two one |
| log(48) | 1.6812 | One point six eight one two |
| log(49) | 1.6902 | One point six nine zero two |
| log(50) | 1.6990 | One point six nine nine zero |
The value of logarithms for numbers 1 to 50, specifically using the base 10 (common logarithm), ranges from log(1) = 0 to log(50) ≈ 1.6990. These values incrementally increase as the numbers rise, reflecting the logarithmic scale’s nature where each unit increase results in progressively smaller increments in the log value. For instance, log(10) = 1, log(20) ≈ 1.3010, and log(30) ≈ 1.4771. This progression illustrates how logarithms transform multiplicative relationships into additive ones, making them invaluable in various mathematical and scientific applications for simplifying complex calculations.
Share :
