Geometry

What is Geometry?

Geometry is a branch of mathematics that deals with the study of shapes, sizes, and the properties of space. It focuses on the relationships between points, lines, surfaces, and solids in a way that reveals their nature and interactions.

Types of Geometry

Type	Description	Applications
Euclidean Geometry	Studies flat, 2D spaces, where the basic elements are points, lines, and planes, and follows Euclid’s postulates.	Architecture, engineering, and map design
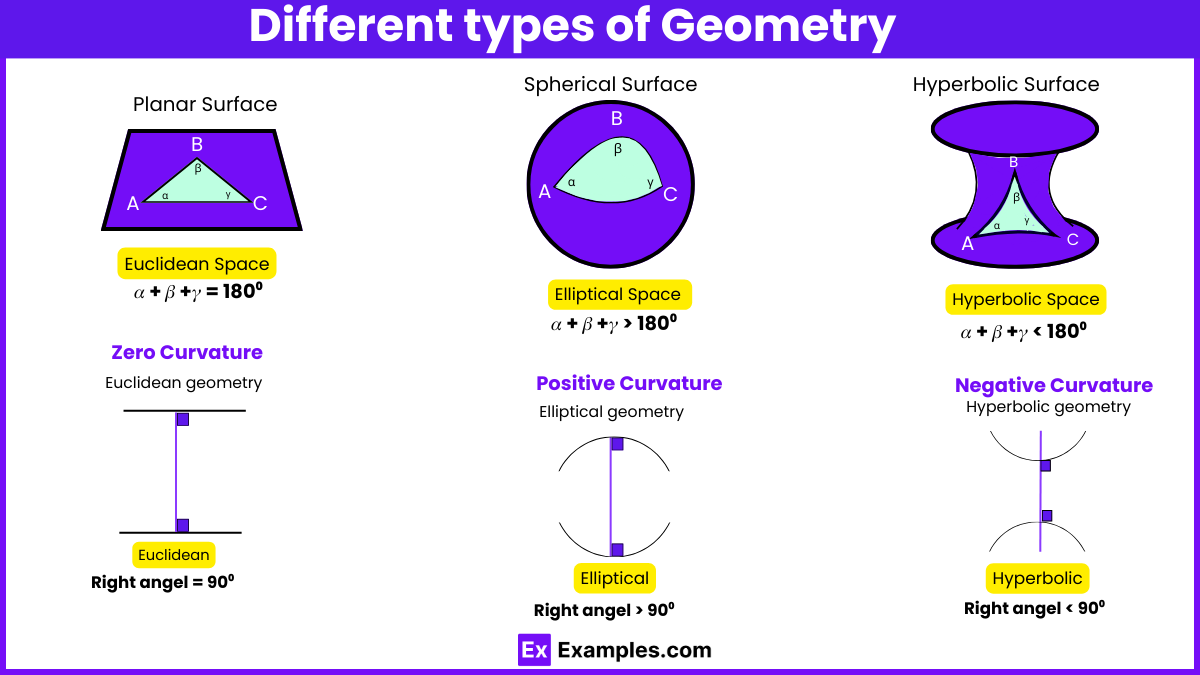
Non-Euclidean Geometry	Explores curved spaces, including hyperbolic (negative curvature) and elliptic (positive curvature) geometries.	Cosmology, GPS systems, and general relativity theory
Analytic Geometry	Uses coordinates and algebraic equations to describe geometric properties and relationships between points, lines, etc.	Computer graphics, robotics, and data visualization
Differential Geometry	Studies geometric properties using calculus, focusing on curves and surfaces and their curvature.	Physics, particularly in relativity and mechanics
Projective Geometry	Deals with properties of figures that remain invariant under projection, studying relationships between points and lines.	Art, perspective drawing, and optical systems
Discrete Geometry	Examines geometric structures in discrete sets, such as points, graphs, and networks.	Computer science, combinatorics, and network design
Fractal Geometry	Studies irregular shapes that display self-similarity at different scales.	Computer graphics, modeling natural phenomena, and art
Topology	Explores properties of spaces that remain invariant under continuous transformations, like stretching or twisting.	Theoretical physics, knot theory, and complex systems

Euclidean Geometry

Euclidean Geometry forms the foundation of the study of geometry. This branch focuses on the properties of plane and solid figures, deriving insights from axioms and theorems. Here are the key aspects of Euclidean Geometry:

1. Fundamental Concepts:
   • Points and Lines: The simplest elements in geometry, representing positions and linear connections between points.
   • Axioms and Postulates: Euclidean Geometry is built on basic, self-evident statements known as axioms and postulates, which underpin more complex theorems and proofs.
   • Geometrical Proof: Logical steps used to demonstrate or verify relationships between geometric figures.
   • Euclid’s Fifth Postulate: A specific foundational statement that deals with parallel lines and has led to significant developments in geometry.
2. Five Basic Postulates: These postulates define and shape Euclidean Geometry:
   1. Connecting Points: A straight line segment can be drawn connecting any two points.
   2. Infinite Extension: Any straight line can be extended indefinitely in both directions.
   3. Drawing Circles: A circle can be drawn with any point as its center and any length as its radius.
   4. Right Angles: All right angles are congruent (i.e., equal).
   5. Parallel Lines: Any two straight lines are parallel if they are equidistant from each other at two points.

Euclid’s Axioms:

Axioms or postulates form the foundational assumptions in geometry, which are universally accepted without requiring proof. Below are several of Euclid’s axioms in geometry, which serve as key building blocks:

1. Equality Transitivity:
   Things equal to the same things are equal to each other.
   Example: If 𝐴=𝐶and 𝐵=𝐶, then A=B.
2. Addition of Equals:
   If equals are added to equals, the wholes are equal.
   Example: If A=B and C=D, then 𝐴+𝐶=𝐵+𝐷
3. Subtraction of Equals:
   If equals are subtracted from equals, the remainders are equal.
   Example: If 𝐴=𝐵 and 𝐶=𝐷, then 𝐴−𝐶=𝐵−𝐷.
4. Coinciding Equals:
   Things that coincide or overlap are equal to one another.
5. Part-Whole Relationship:
   The whole is greater than its part.
   Example: If 𝐴>𝐵, there exists a 𝐶C such that 𝐴=𝐵+𝐶.
6. Doubles of the Same:
   Things that are double the same thing are equal to one another.
   Example: If 𝐴=B, then 2𝐴=2𝐵.
7. Halves of the Same:
   Things that are halves of the same thing are equal to each other.
   Example: If 𝐴=𝐵, then 𝐴2=𝐵2​.

Non-Euclidean Geometries: Spherical and Hyperbolic

Non-Euclidean geometry encompasses geometries that differ from Euclidean geometry, particularly in their treatment of parallel lines and angles within planar spaces. Here’s a look at the two main types:

1. Spherical Geometry:
   This is the study of geometry on a spherical surface. In this geometry:
   • Lines: Are defined as the shortest distance between two points and take the form of arcs known as great circles.
   • Triangles: The sum of the angles in a triangle on a sphere is greater than 180º.
   Spherical geometry is particularly relevant in navigation, astronomy, and earth sciences, as it reflects the nature of our world.
2. Hyperbolic Geometry:
   This type of geometry deals with surfaces that curve inward. In this geometry:
   • Triangles: The sum of the angles in a planar triangle is less than 180º.
   • Applications: Hyperbolic geometry has applications in topology, where it helps describe and understand various curved surfaces and their properties.

Plane Geometry

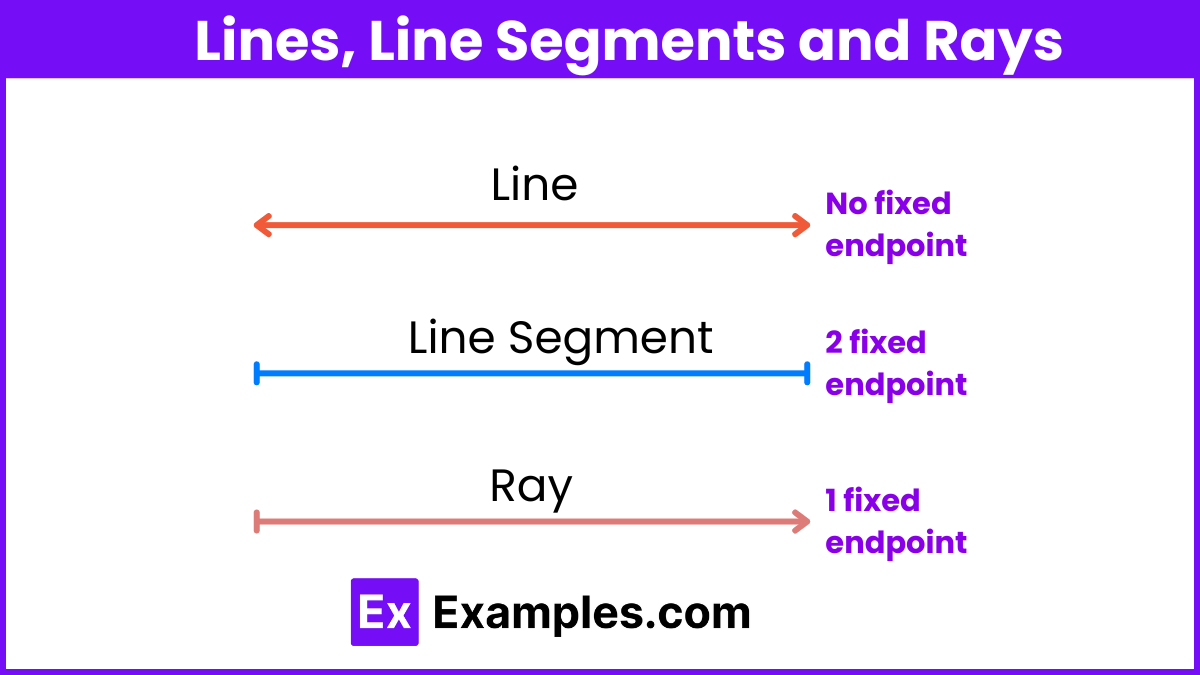
Euclidean Geometry primarily deals with the study of geometry on a plane, a two-dimensional surface that extends infinitely in both directions. Here are some key aspects:

1. The Plane:
   The plane serves as a foundational concept in geometry, acting as a 2D surface that supports various geometric entities and is crucial in fields like graph theory.
2. Basic Components:
   The fundamental components of a plane in Euclidean geometry include:
   • Points: Zero-dimensional units representing locations. Points that lie on the same line are collinear.
   • Lines: One-dimensional entities formed by a set of points extending infinitely in both directions. Lines can intersect or run parallel and are often the intersection of two planes.
   • Angles: Formed by two intersecting lines, angles are a key feature in describing the relationships between lines.
3. Differentiating Between Lines:
   It’s essential to distinguish between different types of lines:
   • Line: Extends infinitely in both directions and has no endpoints.
   • Line Segment: Has a defined start and end point.
   • Ray: Has a start point and extends infinitely in one direction.
4. Relationships Between Lines:
   Lines can have various relationships:
   • Parallel: They never intersect and remain equidistant.
   • Perpendicular: They intersect at a right angle.
   • Intersecting: Lines that cross each other at any angle.

Angles in Geometry

When two straight lines or rays intersect at a point, they form an angle. Angles are measured in degrees and can take on various forms, including acute, right, obtuse, straight, or reflex angles. In terms of relationships, pairs of angles can be complementary, summing to 90º, or supplementary, summing to 180º. The construction and study of angles and lines are integral to the field of geometry, serving as foundational elements. Additionally, exploring angles within a unit circle or a triangle lays the groundwork for trigonometry, bridging geometry and trigonometric functions. Furthermore, the concept of transversals and related angles provides insights into the properties and theorems associated with parallel lines, enhancing the understanding of geometric relationships.

Plane Shapes in Geometry

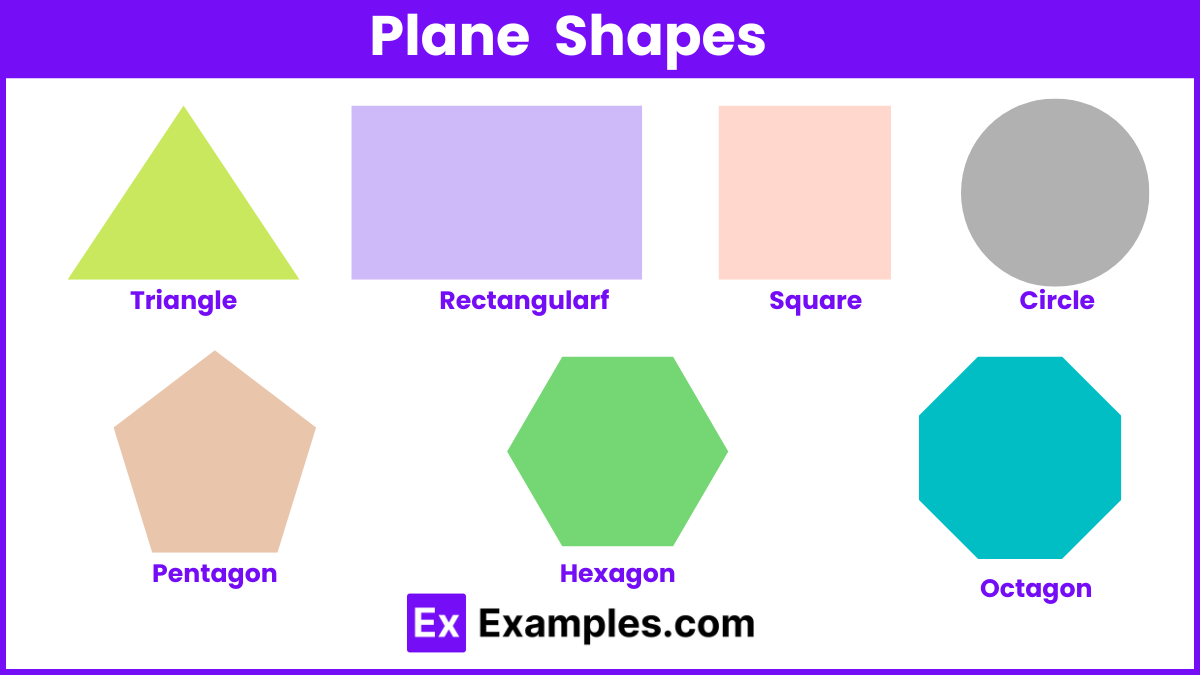
Plane shapes are two-dimensional or flat geometric figures that are essential for classifying and understanding the properties of various geometric forms. Polygons are closed curves composed of more than two lines, and one key example is the triangle, a closed figure with three sides and three vertices. Numerous theorems have been developed around triangles to explore their properties in depth, including:

• Heron’s Formula for calculating area
• The Exterior Angle Theorem
• The Angle Sum Property
• The Basic Proportionality Theorem
• The Similarity and Congruence in Triangles
• The Pythagorean Theorem

These theorems clarify relationships between angles and sides within triangles. Another key plane shape is the quadrilateral, which is a polygon with four sides and four vertices.

Solid Geometry

Solid shapes in geometry are three-dimensional figures characterized by length, width, and height. Various types of solids exist, including cylinders, cubes, spheres, cones, cuboids, prisms, and pyramids, each of which occupies space and has distinct features:

• Characteristics: Solids are defined by their vertices (corner points), faces (flat surfaces), and edges (lines connecting vertices).
• Platonic Solids and Polyhedrons: In Euclidean space, the five Platonic solids and various polyhedrons exhibit unique and interesting properties, contributing to the study of solid geometry.
• Nets and Solid Construction: Nets of plane shapes can be folded to form solids, providing a bridge between two-dimensional and three-dimensional geometry.

Measurement in Geometry

Measurement in geometry plays a crucial role in understanding and quantifying the properties of various geometric figures. Here are the key aspects:

1. Length and Distance:
   Measurement of length and distance is fundamental to geometry, helping to define the size of line segments, the distance between points, and the perimeters of shapes.
2. Area:
   Area measures the 2d-space enclosed by a figure, such as squares, rectangles, circles, and polygons. Formulas like 𝐴=𝑙×𝑤 for a rectangle or 𝐴=1/2×𝑏×ℎ for a triangle simplify these calculations.
3. Volume:
   Volume measures the three-dimensional space occupied by a solid shape, such as cubes, spheres, or cylinders. For instance, the volume of a cube is 𝑉=𝑠³ (where 𝑠s is the length of a side), while the volume of a cylinder is 𝑉=𝜋𝑟²ℎ (where 𝑟r is the radius of its base and ℎ its height).
4. Angles:
   Angles are another key measurement in geometry, defined in degrees or radians. Angles help characterize the relationships between intersecting lines or the internal angles of polygons.
5. Coordinate Systems:
   In analytic geometry, measurements are often facilitated by coordinate systems, which provide a way to quantify positions and distances between points using numerical coordinates.

Geometry Formulas

Geometry formulas are essential tools that help quantify the properties of various geometric figures. Here are key formulas for different shapes:

1. Area:
   • Rectangle: 𝐴=𝑙×𝑤
   • Triangle: 𝐴=1/2×𝑏×ℎ
   • Circle: 𝐴=𝜋𝑟²
   • Parallelogram: 𝐴=𝑏×ℎ
2. Perimeter:
   • Rectangle: 𝑃=2(𝑙+𝑤)P=2(l+w)
   • Triangle: 𝑃=𝑎+𝑏+𝑐 (where 𝑎,𝑏, and 𝑐 are the lengths of the sides)
   • Circle: 𝐶=2𝜋𝑟 (Circumference)
3. Volume:
   • Cube: 𝑉=𝑠³
   • Rectangular Prism: 𝑉=𝑙×𝑤×ℎ
   • Cylinder: 𝑉=𝜋𝑟²ℎ
   • Sphere: 𝑉=43𝜋𝑟³
   • Cone: 𝑉=13𝜋𝑟²ℎ
4. Surface Area:
   • Cube: 𝑆𝐴=6𝑠²
   • Rectangular Prism: 𝑆𝐴=2𝑙𝑤+2𝑙ℎ+2𝑤ℎ
   • Sphere: 𝑆𝐴=4𝜋𝑟²
   • Cylinder: 𝑆𝐴=2𝜋𝑟(ℎ+𝑟)
5. Pythagorean Theorem:
   • In a right triangle with legs a and b, and hypotenuse 𝑐: 𝑎²+𝑏²=𝑐²

Shape	Formulas
Right Triangle	Pythagorean Theorem: 𝑏²+ℎ²=𝑐² (where 𝑏 is base, ℎ is height, 𝑐 is hypotenuse) Area: 𝐴=1/2𝑏×ℎ Perimeter: 𝑃=𝑏+ℎ+𝑐
Triangle	Perimeter: 𝑃=𝑎+𝑏+𝑐 Area: 𝐴=1/2𝑏×ℎ (where 𝑎,𝑏,𝑐a are sides)
Rectangle	Perimeter: 𝑃=2(𝑙+𝑤) Area: 𝐴=𝑙𝑤 Diagonal: 𝑑=√𝑙²+𝑤²(where 𝑙l is length, 𝑤w is width)
Parallelogram	Perimeter: 𝑃=2(𝑎+𝑏) (where 𝑎,𝑏 are sides) Area: 𝐴=𝑏×ℎ Height: ℎ=𝐴𝑏​ Base: 𝑏=𝐴ℎ​
Trapezium	Area: 𝐴=12(𝑎+𝑏)ℎ (where 𝑎,𝑏 are parallel sides, ℎ is the distance between them)
Circle	Circumference: 𝐶=2𝜋𝑟 Area: 𝐴=𝜋𝑟² Diameter: 𝑑=2𝑟 (where r is radius)
Square	Perimeter: 𝑃=4𝑎 Area: 𝐴=𝑎² Diagonal: 𝑑=𝑎² Side: 𝑎=𝐴​
Arc	Arc Length: 𝐿=𝑟𝜃(where 𝜃 is the central angle in radians, 𝑟 is radius)
Cube	Area: 𝐴=6𝑎² Volume: 𝑉=𝑎³ Edge: 𝑎=𝑉³​ Space Diagonal: 𝑑=𝑎³
Cuboid	Surface Area: 𝐴=2(𝑙𝑏+𝑏ℎ+ℎ𝑙) Volume: 𝑉=𝑙𝑏ℎ Space Diagonal: 𝑑=√𝑙²+𝑏²+ℎ²​ (where 𝑙 is length, 𝑏 is breadth, ℎ is height)
Cylinder	Total Surface Area: 𝐴=2𝜋𝑟ℎ+2𝜋𝑟² Curved Surface Area: 𝐴𝑐=2𝜋𝑟ℎ Volume: 𝑉=𝜋𝑟²ℎ Base Area: 𝐴𝑏=𝜋𝑟² Radius: 𝑟=𝑉𝜋ℎr=πhV​​
Cone	Total Surface Area: 𝐴=𝜋𝑟(𝑟+𝑙)=𝜋𝑟[𝑟+ℎ²+𝑟²] Curved Surface Area: 𝐴𝑐=𝜋𝑟𝑙 Volume: 𝑉=13𝜋𝑟²ℎ Slant Height: 𝑙=ℎ²+𝑟² Base Area: 𝐴𝑏=𝜋𝑟²
Sphere	Surface Area: 𝐴A=4πr² Volume: 𝑉=43𝜋𝑟³ Diameter: 𝑑=2𝑟

Problem 1

A right triangle has a base of 6 units and a height of 8 units. Calculate its area, perimeter, and the length of the hypotenuse.

Solution:

• Area:
  𝐴=1/2×6×8=24 square units

• Hypotenuse:
  ℎ=√ 6²+8²=√36+64=√100=10 units

• Perimeter:
  𝑃=6+8+10=24 units

Problem 2

A rectangle has a length of 10 units and a width of 4 units. Find its area, perimeter, and the length of its diagonal.

Solution:

• Area:
  𝐴=10×4=40 square units

• Perimeter:
  𝑃=2(10+4)=2×14=28 units

• Diagonal:
  𝑑=√10²+4²=√100+16=√116≈10.77 units

Problem 3

A circle has a radius of 7 units. Calculate its area and circumference.

Solution:

• Area:
  𝐴=𝜋𝑟²=𝜋×7²=𝜋×49≈153.94 square units

• Circumference:
  𝐶=2𝜋𝑟=2×𝜋×7=14×𝜋≈43.98units

Problem 4

A trapezium has two parallel sides of length 8 units and 4 units, with a distance of 5 units between them. Find its area.

Solution:

• Area:
  𝐴=1/2(8+4)×5=1/2×12×5=30 square units

Problem 5

A cylinder has a radius of 3 units and a height of 7 units. Find its volume and total surface area.

Solution:

• Volume:
  𝑉=𝜋𝑟²ℎ=𝜋×3²×7=𝜋×9×7=63×𝜋≈197.92 cubic units

FAQs

Is Geometry Harder Than Algebra?

Geometry and algebra differ in approach. While algebra deals with abstract symbols and equations, geometry focuses on shapes, figures, and spatial relationships. Which is harder depends on individual preferences: those comfortable with visual and spatial reasoning may find geometry easier, while algebra may suit others better.

What Is the Basic Math Geometry?

Basic math geometry involves the study of shapes, sizes, and spatial relationships in two-dimensional and three-dimensional spaces. This includes foundational concepts like points, lines, angles, and planes, as well as formulas for calculating areas, perimeters, and volumes of various figures like triangles, rectangles, and circles.

What Grade Level Is Geometry?

Geometry is typically introduced around 8th to 10th grade, depending on the educational curriculum. In these grades, students learn about plane and solid geometry, exploring the properties of various shapes, theorems, and formulas, which provides a foundation for more advanced studies.

Is Geometry 10th Grade?

In many educational systems, geometry is often taught in 10th grade. This course covers a range of topics, including basic geometric principles, properties of shapes, and proofs, along with formulas for calculating area, volume, and other measurements, providing students with foundational geometric knowledge.

What Is the Hardest Math Class?

The hardest math class varies by individual and curriculum. For many, advanced classes like calculus, linear algebra, or differential equations can pose significant challenges due to abstract concepts and complex calculations. However, difficulty depends on the student’s background, skills, and comfort with different types of math.