Calculus

Calculus is a crucial branch of mathematics that deals with the concepts of rate of change and motion. The two main pillars of calculus are derivatives and integrals:

1. Derivatives: The derivative of a function measures its rate of change at a specific point. It provides insight into how the function behaves in a local context.
2. Integrals: The integral of a function measures the area under its curve, accumulating the discrete values of the function over a range of values. This helps in understanding the total effect or accumulation over a given range.

Calculus is also known as infinitesimal calculus or “the calculus of infinitesimals,” referring to the study of continuous changes using quantities nearly equal to zero but not exactly zero. This classical approach helps to analyze and understand the continuous changes in function

What is Calculus?

Calculus in mathematics is essential for constructing mathematical models that provide optimal solutions.Calculus focuses on some important topics covered in math such as differentiation, integration, limits, functions, and so on. Calculus, a branch of mathematics

Calculus in Mathematics

Branches of Calculus

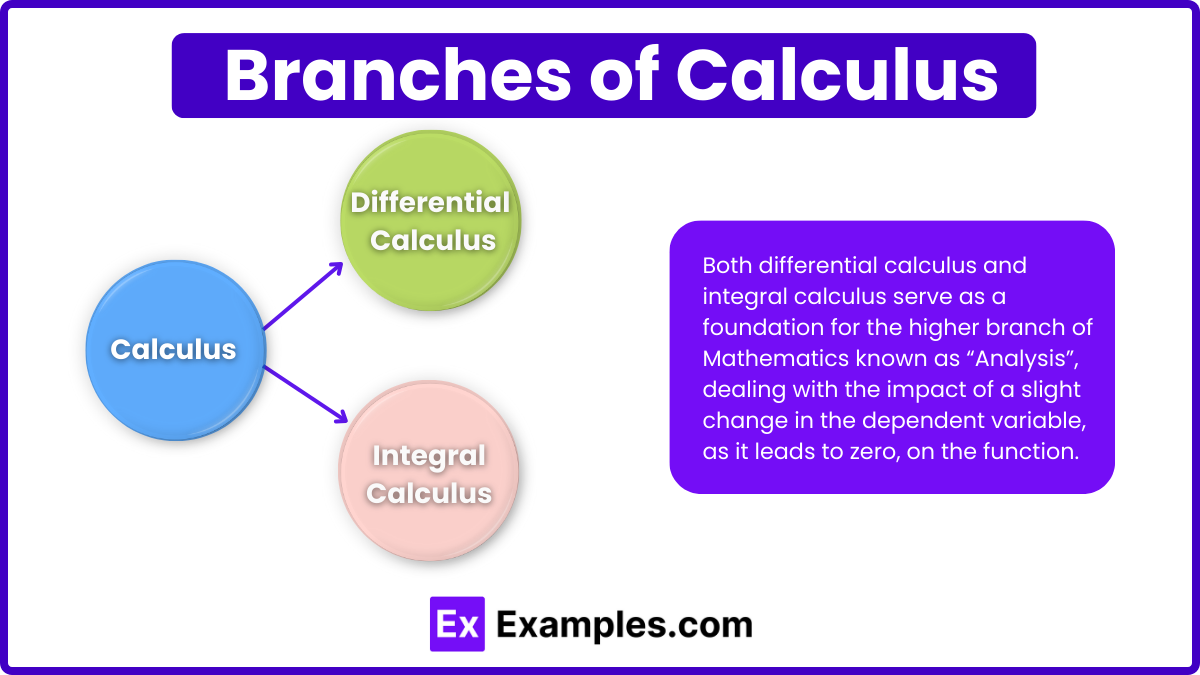
Calculus is a fundamental branch of mathematics that deals with the study of rates of change and the accumulation of quantities. It is divided into two main areas:

1. Differential Calculus: This deals with the concept of a derivative, which measures how a function changes as its input changes. In simpler terms, the derivative gives the rate of change of a function at any given point. This concept is crucial for understanding how variables are related and how they interact over time, making it essential for various fields like physics, engineering, and economics.
2. Integral Calculus: This involves the concept of an integral, which represents the accumulation of quantities, such as area under a curve or the total accumulated value over time. Integrals are used to compute areas, volumes, and other quantities that accumulate over a range.

Functions of Calculus

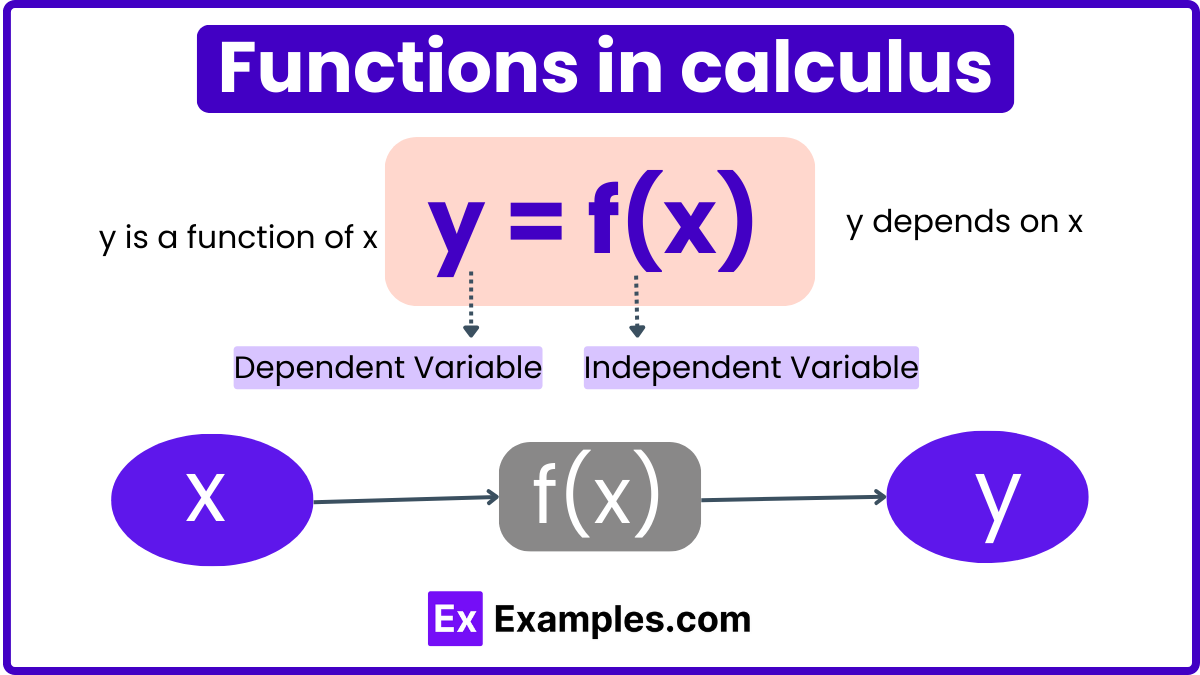
In calculus, functions describe the relationship between two variables: the independent variable and the dependent variable. Let’s explore this concept more clearly:

1. Independent Variable: This is the input or variable that can be freely chosen. It’s often denoted by 𝑥x or 𝑡t in equations. The independent variable represents factors that influence or drive the dependent variable. For example, in a function modeling the distance traveled by a car over time, time would be the independent variable.
2. Dependent Variable: This is the output or result that depends on the independent variable. It’s usually denoted by 𝑦y or 𝑓(𝑥)f(x). The dependent variable reflects how the independent variable affects it. In the car example, distance would be the dependent variable, as it changes in response to the time elapsed.

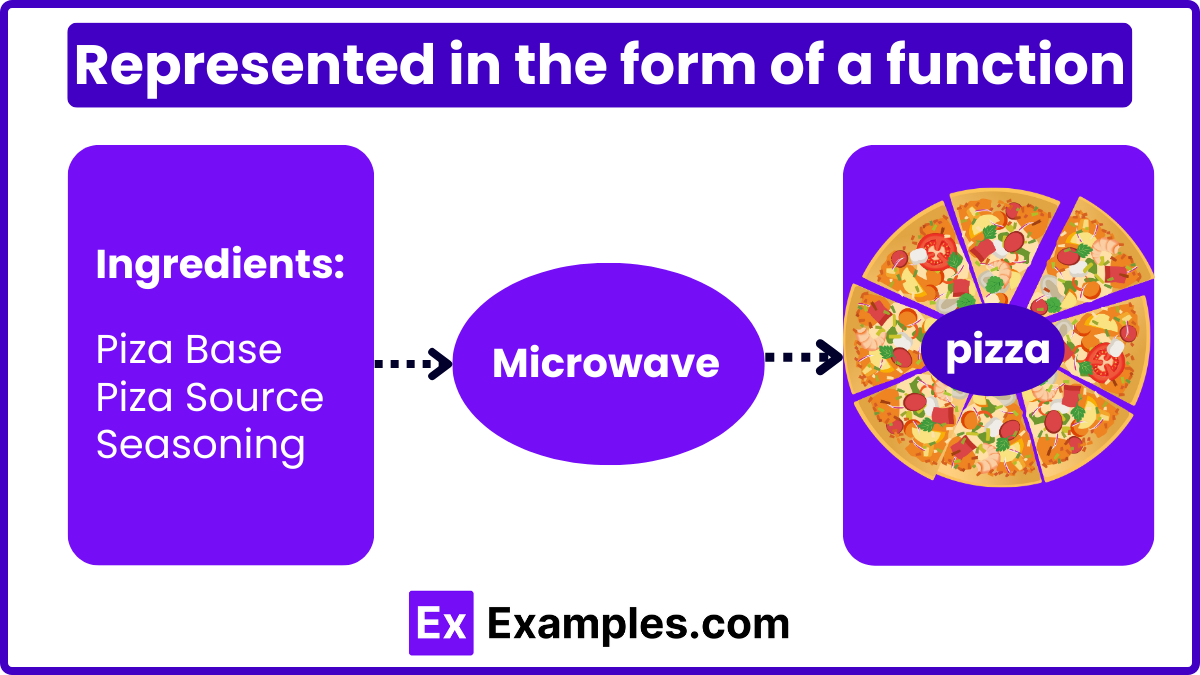
Let’s simplify the concept of a function using the example of making a pizza:

1. Inputs: Just like a function has inputs, making a pizza also starts with essential ingredients. For instance, to make a pizza, you need:
   • A pizza base
   • Pizza sauce
   • Cheese
   • Seasonings
2. Function: The process of making a pizza can be viewed as a function that takes these ingredients (inputs) and transforms them into a final product. The “pizza-making function” involves steps such as assembling the ingredients, applying the sauce, adding cheese, sprinkling seasonings, and baking the pizza.
3. Output: The output of this function is the finished pizza, ready to enjoy. Similarly, in calculus, the output of a function depends on how it processes its inputs.

Let’s take another example

Suppose that: y = x³

Value of x	Value of y
1	1
2	9
9	729
11	1331

Differential Calculus

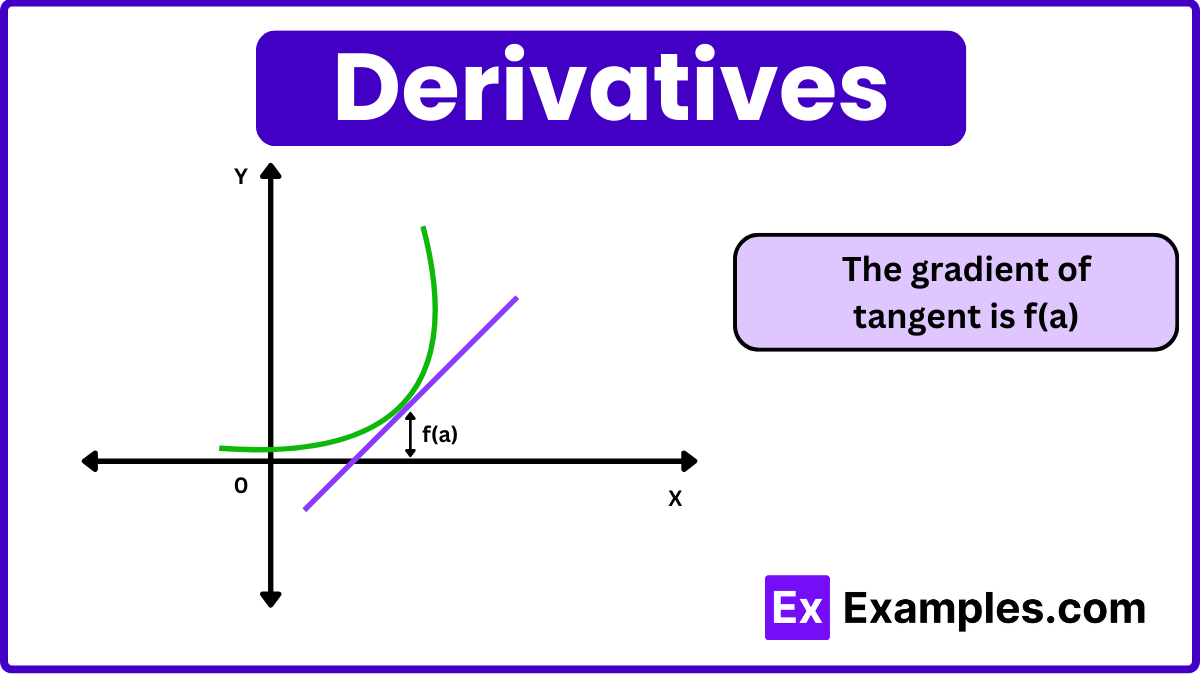
Differential calculus deals with finding the rate of change of a function with respect to its variables. Here are its key components:

1. Derivatives: Derivatives measure the instantaneous rate of change of a function. For a function 𝑓(𝑥), the derivative with respect to 𝑥 is denoted by 𝑑𝑓/𝑑𝑥​ or 𝑓′(𝑥). The process of finding a derivative is called differentiation.
   • Optimal Solutions: Derivatives help find the maxima and minima of functions, allowing us to optimize solutions in various fields such as economics, physics, and engineering.
   • Deltas and Differentials: In calculus, 𝑑𝑥 and 𝑑𝑦 are known as differentials, representing small changes in variables 𝑥 and 𝑦 respectively.
2. Limits: Limits describe the value a function approaches as its input nears a specific point. They provide the foundation for derivatives and continuity. The limit of a function 𝑓(𝑥) as 𝑥 approaches 𝑐 is expressed as:

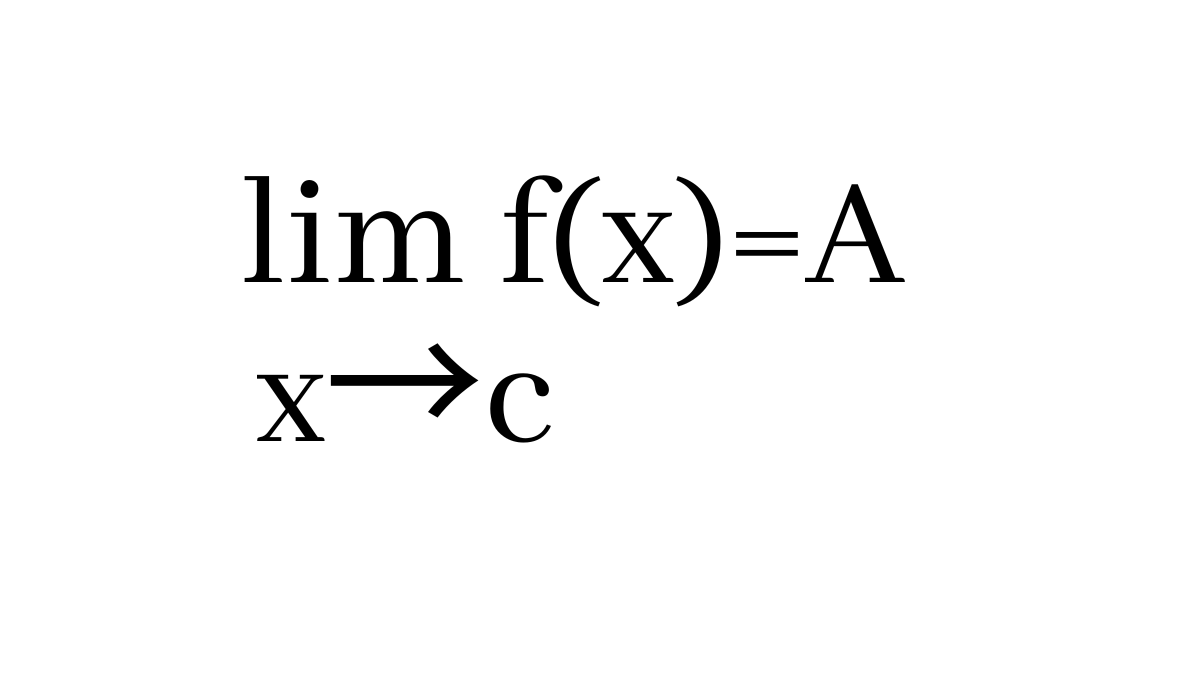
This means the function 𝑓(𝑥) approaches 𝐴 as 𝑥 gets closer to 𝑐.

1. Continuity: A function 𝑓(𝑥) is continuous at 𝑥=𝑎 if the following conditions are met:
   • 𝑓(𝑎) is defined,
   • lim⁡ₓ→꜀𝑓(𝑥)exists,
   • lim⁡ₓ→꜀𝑓(𝑥)=𝑓(𝑎)
2. Continuity and Differentiability: If a function is differentiable at a point, it is also continuous at that point. However, the reverse is not necessarily true: a function can be continuous at a point without being differentiable there.

Integral Calculus

Integral calculus is the study of integrals and their properties, offering powerful tools for various applications:

1. Integration: Integration is the reverse process of differentiation. While differentiation breaks down a function into smaller parts, integration combines these parts to form a whole. It is especially useful for:
   • Reconstructing Functions: Integration can calculate a function 𝑓(𝑥) from its derivative 𝑓′(𝑥).
   • Calculating Areas: Integration is a key method for finding the area under a curve of a given function.

Indefinite Integral: An indefinite integral doesn’t specify upper or lower limits, representing a general form of integration. Because of this, it includes an integration constant 𝐶:

∫f(x)dx=F(x)+C

Here, 𝐹(𝑥) is the antiderivative of 𝑓(𝑥), meaning 𝐹′(𝑥)=𝑓(𝑥).

Definite Integral: A definite integral has specific upper and lower limits, allowing it to compute the exact area under a curve between these bounds. It’s represented as:

∫ₐᵇ ​f(x) dx=F(b)−F(a)

This gives the area between the function 𝑓(𝑥) and the x-axis from 𝑥=𝑎 to 𝑥=𝑏.

Calculus Formula

Calculus formulas can be broadly divided into the following six broad sets of formulas. The six broad formulas are related to limits, differentiation, integration, definite integrals, application of differentiation, and differential equations.

Limits Formulas: Limit formulas assist in finding the value a function approaches as its input nears a specific point, allowing for precise approximations of the function’s behavior at that point.

lim_ₓ→₀ (x^ⁿ – a^ⁿ )(x – a) = na^{⁽ⁿ ⁻ ¹⁾}
limₓ→₀ (sin x)/x = 1
lim_ₓ→₀ (tan x)/x = 1
limₓ→₀ (e^ˣ – 1)/x = 1
limₓ→₀ (aˣ – 1)/x = log_ₑᵃ
lim_ₓ→∞ (1 + (1/x))ˣ = e
lim_ₓ→₀ (1 + x)¹/ˣ = e
lim_ₓ→₀ (1 + (a/x))ˣ = eᵃ

Differentiation Formulas: Differentiation Formulas are applicable for algebraic expressions, trigonometric ratios, inverse trigonometry, and exponential terms.

d/dx (xⁿ ) = nxⁿ ⁻ ¹
d/dx (Constant) = 0
d/dx (eˣ) = eˣ
d/dx (aˣ = a · ln a
d/dx (ln x) = 1/x
d/dx (sin x) = cos x
d/dx (cos x) = -sin x
d/dx (tan x) = sec²x
d/dx (cot x) = -cosec²x
d/dx (sec x) = sec x · tan x
d/dx (cosec x) = -cosec x · cot x

Integration Formula: Integrals formulas can be derived from differentiation formulas, and are complimentary to differentiation formulas.

∫ xⁿ dx = xⁿ⁺¹/(n + 1) + C
∫ 1 dx = x + C
∫ e^x dx = e^x + C
∫(1/x) dx = ln |x| + C
∫ aˣ dx = (aˣ/log a) + C
∫ cos x dx = sin x + C
∫ sin x dx = -cos x + C
∫ sec²x dx = tan x + C
∫ cosec²x dx = -cot x + C
∫ sec x tan x dx = sec x + C
∫ cosec x cot x dx = -cosec x + C

Definite Integrals Formulas:

∫ᵇₐ f'(x) dx = f(b) – f(a), this is known as fundamental theorem of calculus
∫ᵇₐ f(x) dx = ∫ᵇₐ f(t) dt
∫ᵇₐ f(x) dx = – ∫ᵃ₆f(x) dx
∫ᵇₐ f(x) dx = ∫ᶜₐ f(x) dx + ∫ᵇ꜀ f(x) dx
∫ᵇₐ f(x) dx = ∫ᵇₐ f(a + b – x) dx
∫ᵇ₀ f(x) dx = ∫ᵃ₀  f(a – x) dx
∫ᵇ₋ₐ f(x) dx = 2∫ᵃ₀ f(x) dx, f is an even function
∫ᵇ₋ₐ f(x) dx = 0 , f is an odd function

Application of Differentiation Formulas: 

Differentiation formulas are valuable for a range of applications. They help approximate and estimate values, and can be used to find equations of tangents and normals to a curve at a given point. Additionally, they allow us to calculate maxima and minima, enabling optimization in various fields. Differentiation is also essential for understanding the rates of change in numerous physical events, from motion and growth to economic trends and more.

dy/dx = (dy/dt)/(dx/dt)
Equation of a Tangent: y – y_₁ = dy/dx · (x – x₁)
Equation of a Normal: y – y₁ = -1/(dy/dx) · (x – x₁)

Differential Equations Formula: Differential equations are equations that involve derivatives, capturing the relationship between changing variables. In these equations, the unknown function 𝑦 is represented as a function of the variable 𝑥. The derivative 𝑑𝑦/𝑑𝑥​ serves as a key component of the equation, describing the rate at which 𝑦 changes concerning 𝑥. Differential equations are fundamental tools for modeling dynamic systems and capturing how variables interact over time.

Homogeneous Differential Equation: f(λx, λy) = λⁿf(x, y)
Linear Differential Equation: dy/dx + Py = Q. The general solution of linear differential equation is y.e^{– ∫ᴾ ᵈˣ} = ∫(Q · e^{∫ᴾ ᵈˣ} ) dx + C

Practice Problems

Question:

A function 𝑓(𝑥) is defined as 𝑓(𝑥)=3𝑥²−4𝑥+1

1. Calculate the first derivative of this function.
2. Determine the value of the derivative when 𝑥=2
3. Interpret the meaning of this value in the context of the function.

Answer:

1. The first derivative of the function 𝑓(𝑥) is:

f′'(x) = d​/dx(3x²−4x+1) = 6x−4

2. Substituting 𝑥=2x=2 into the derivative:

f′'(2)=6(2)−4=12−4=8

1. The value 𝑓′(2)=8 represents the instantaneous rate of change of the function 𝑓(𝑥) at 𝑥=2. In other words, it indicates how quickly the value of 𝑓(𝑥) is increasing or decreasing at that point. Here, it shows that the function is increasing at a rate of 8 units per unit change in 𝑥 when 𝑥=2.

Question: Evaluate the definite integral ∫³₁(2𝑥+1) 𝑑𝑥

Answer: The definite integral is computed by finding the antiderivative of the function 2𝑥+1 and then evaluating it at the specified limits:

∫³₁(2x+1)dx = [x²+x]³₁

Evaluating at 𝑥=3 and 𝑥=1:

=(3²+3)−(1²+1)

= (9+3)−(1+1)

= 12−2

= 10

Therefore, the value of the definite integral ∫​³₁(2x+1)dx is 10.

Question: Solve the differential equation 𝑑𝑦/𝑑𝑥=2𝑥 by finding the general solution.

Answer: This is a first-order differential equation, which can be solved by integrating both sides:

𝑑𝑦/𝑑𝑥 = 2𝑥 ⟹ dy = 2x dx

Integrating the right side with respect to 𝑥:

∫dy = ∫2x dx

y=x²+C

Therefore, the general solution to the differential equation 𝑑𝑦/𝑑𝑥=2𝑥 is 𝑦=𝑥²+𝐶, where C is the integration constant.

FAQs

Is Calculus Very Hard?

Calculus can be challenging initially due to its abstract nature and concepts like limits, derivatives, and integrals. However, with practice, it becomes more intuitive, as it provides tools for solving real-world problems and understanding the relationships between changing variables.

What Is Calculus in Simple Terms?

Calculus is the branch of mathematics that deals with change and motion. It consists of two main areas: differential calculus, which examines how functions change at a specific point, and integral calculus, which accumulates or aggregates quantities to compute total values or areas.

What Is Calculus vs. Algebra?

Algebra focuses on manipulating and solving equations with known and unknown variables, using operations such as addition and multiplication. Calculus builds on algebra, exploring how functions change over time, how they can be integrated to compute areas, and how to model and optimize relationships between variables.

What Is the Basic Calculus For?

Basic calculus helps understand and model changes in various fields. It finds the rate of change of functions, accumulates quantities over time, and provides solutions for optimizing systems. Applications include science, engineering, economics, and finance, helping to solve complex problems and model dynamic systems.

What’s Harder, Algebra or Calculus?

Calculus may be more challenging than algebra for some, as it introduces new concepts like limits, derivatives, and integrals. However, algebra provides foundational skills needed for calculus. The difficulty depends on an individual’s familiarity with abstract concepts and mathematical reasoning.