What is the standard form of a quadratic equation?
ax^2 + bx + c = 0
ax^2 + b = c
x^2 + b = c
ax + b = c


There are many proven mathematical equations we can observe in our everyday life that has many practical uses and applications. The quadratic equation is one of the most well-known types of math equation people will encounter in their lives.
A quadratic equation is a polynomial equation of the form ax²+bx+c=0 , where a, b, and c are constants, and a≠0 .It represents a parabolic curve in a graph and is crucial in various mathematical and real-world applications. Solutions to quadratic equations can be found using methods such as factoring, completing the square, or the quadratic formula.

The quadratic equation is termed univariate because it involves only one variable, x. The exponents of x are non-negative integers, classifying it as a equation of polynomials. The highest power of x in a quadratic equation is 2, hence it is called a quadratic polynomial.
The solutions to this equation are the values of x that satisfy it, also known as the zeros or roots of the polynomial. In the case of a quadratic equation, there are typically two such roots. Substituting these root values back into the left-hand side of the equation will result in zero, confirming them as zeros of the polynomial
Factoring: This involves expressing the quadratic equation ax²+bx+c=0 as the product of two binomials. This method works well when the equation can be easily factored into simpler binomials. If the quadratic can be factored, you set each factor equal to zero and solve for x.
Completing the Square: Completing the square transforms the quadratic equation into a perfect square trinomial, making it easier to solve. This method involves:
Quadratic Formula: This is a universal method that can solve any quadratic equation. The formula is derived from completing the square of the general quadratic equation and is given by:
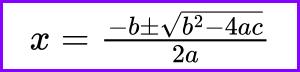
Here, a, b, and c are the coefficients of the equation ax²+bx+c=0. The term under the square root, b²−4ac, is known as the discriminant and provides information about the nature and number of the roots.
Graphical Method: By graphing the quadratic equation y=ax²+bx+c, you can visually find the roots of the equation (the points where the graph crosses the x-axis). This method is useful for getting an approximate idea of the solutions and understanding the behavior of the quadratic function.
Basic Quadratic Equation: x²−5x+6=0 This equation can be factored into (x−2)(x−3)=0, with solutions x=2 and x=3.
Quadratic with Negative Coefficients: −3x²+12x−9=0 Factoring out the common factor, it simplifies to −3(x²−4x+3)=0 or further to −3(x−1)(x−3)=0, with roots x=1.
Quadratic with a Leading Coefficient Greater Than One: 2x²−8x+6=0 This equation can be simplified by factoring or using the quadratic formula, yielding roots which simplify to x=1 and x=3 after factoring as 2(x−1)(x−3)=0.
Quadratic with No Real Roots: x²+4x+8=0 Using the quadratic formula, the discriminant (b²−4ac) is negative (16−32=−16), indicating that the roots are complex numbers.
Quadratic as a Model of Projectile Motion: h(t)=−16t²+40t+5 Here, h(t) models the height of a projectile at time t, with a=−16, b=40, and c=5. The roots of the equation, found by setting h(t)=0, tell us when the projectile is at ground level.
Quadratic Relation in Geometry: x²+y²=25 This is the equation of a circle with radius 5, centered at the origin. While not a quadratic in the standard form, it shows the quadratic relationship between x and y coordinates of points on the circle.
Quadratic equations are widely used to solve various real-life problems. When addressing word problems, common applications of quadratic equations include scenarios involving speed, as well as geometric calculations for areas. Here are some specific examples:
The quadratic equation has many practical applications that range from the prices of products, services, and commodities to the range or speed of an object being pushed by mechanical energy and electrical energy. Therefore it is important to know how to use quadratic equations in various themes, tones, and contexts. If you want to learn more about quadratic equations and how to use them, you may use any of the links above.
Problem 1: Solve the quadratic equation x²−7x+10=0
Problem 2: A ball is thrown upwards with an initial velocity of 20 meters per second from a height of 5 meters. The height h of the ball at time t seconds can be modeled by the equation h=−5t²+20t+5. Determine when the ball will hit the ground.
Solution to Problem 1: Factoring the quadratic equation, we get: x²−7x+10=(x−2)(x−5)=0 Thus, x=2 or x=5.
Solution to Problem 2: To find when the ball hits the ground, set h=0:
0=−5t²+20t+5
Using the quadratic formula,
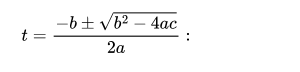


The two types of quadratic formulas are:
The Quadratic Formula for solving equations: x=−b±(b²−4ac)/2a
Three methods to solve quadratic equations are:
Factoring
Using the quadratic formula
Completing the square
The general formula of a quadratic equation is ax²+bx+c=0
No, a quadratic equation can have at most two roots, which might be real or complex, but cannot exceed two distinct solutions.

There are many proven mathematical equations we can observe in our everyday life that has many practical uses and applications. The quadratic equation is one of the most well-known types of math equation people will encounter in their lives.
A quadratic equation is a polynomial equation of the form ax²+bx+c=0 , where a, b, and c are constants, and a≠0 .It represents a parabolic curve in a graph and is crucial in various mathematical and real-world applications. Solutions to quadratic equations can be found using methods such as factoring, completing the square, or the quadratic formula.

The quadratic equation is termed univariate because it involves only one variable, x. The exponents of x are non-negative integers, classifying it as a equation of polynomials. The highest power of x in a quadratic equation is 2, hence it is called a quadratic polynomial.
The solutions to this equation are the values of x that satisfy it, also known as the zeros or roots of the polynomial. In the case of a quadratic equation, there are typically two such roots. Substituting these root values back into the left-hand side of the equation will result in zero, confirming them as zeros of the polynomial
Factoring: This involves expressing the quadratic equation ax²+bx+c=0 as the product of two binomials. This method works well when the equation can be easily factored into simpler binomials. If the quadratic can be factored, you set each factor equal to zero and solve for x.
Completing the Square: Completing the square transforms the quadratic equation into a perfect square trinomial, making it easier to solve. This method involves:
Rearranging the equations to isolate the x² and x terms on one side.
Adding and subtracting the same value to balance the equation and form a perfect square on one side.
Taking the square root of both sides and solving for x.
Quadratic Formula: This is a universal method that can solve any quadratic equation. The formula is derived from completing the square of the general quadratic equation and is given by:
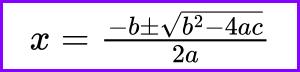
Here, a, b, and c are the coefficients of the equation ax²+bx+c=0. The term under the square root, b²−4ac, is known as the discriminant and provides information about the nature and number of the roots.
Graphical Method: By graphing the quadratic equation y=ax²+bx+c, you can visually find the roots of the equation (the points where the graph crosses the x-axis). This method is useful for getting an approximate idea of the solutions and understanding the behavior of the quadratic function.
Basic Quadratic Equation: x²−5x+6=0 This equation can be factored into (x−2)(x−3)=0, with solutions x=2 and x=3.
Quadratic with Negative Coefficients: −3x²+12x−9=0 Factoring out the common factor, it simplifies to −3(x²−4x+3)=0 or further to −3(x−1)(x−3)=0, with roots x=1.
Quadratic with a Leading Coefficient Greater Than One: 2x²−8x+6=0 This equation can be simplified by factoring or using the quadratic formula, yielding roots which simplify to x=1 and x=3 after factoring as 2(x−1)(x−3)=0.
Quadratic with No Real Roots: x²+4x+8=0 Using the quadratic formula, the discriminant (b²−4ac) is negative (16−32=−16), indicating that the roots are complex numbers.
Quadratic as a Model of Projectile Motion: h(t)=−16t²+40t+5 Here, h(t) models the height of a projectile at time t, with a=−16, b=40, and c=5. The roots of the equation, found by setting h(t)=0, tell us when the projectile is at ground level.
Quadratic Relation in Geometry: x²+y²=25 This is the equation of a circle with radius 5, centered at the origin. While not a quadratic in the standard form, it shows the quadratic relationship between x and y coordinates of points on the circle.
Quadratic equations are widely used to solve various real-life problems. When addressing word problems, common applications of quadratic equations include scenarios involving speed, as well as geometric calculations for areas. Here are some specific examples:
Geometry Problems: Quadratic equations are instrumental in determining the areas of quadrilaterals such as rectangles, parallelograms, and others, where dimensions might depend on quadratic relationships.
Motion Problems: These involve scenarios related to distance, speed, and time, where the relationships can often be described by quadratic equations due to acceleration components or varying speeds.

ncert.nic.in

alamo.edu

math.utah.edu

uww.edu

caps.unm.edu

sites.math.washington.edu

hec.ca

math.uiowa.edu

scg.ac.uk
The quadratic equation has many practical applications that range from the prices of products, services, and commodities to the range or speed of an object being pushed by mechanical energy and electrical energy. Therefore it is important to know how to use quadratic equations in various themes, tones, and contexts. If you want to learn more about quadratic equations and how to use them, you may use any of the links above.
Problem 1: Solve the quadratic equation x²−7x+10=0
Problem 2: A ball is thrown upwards with an initial velocity of 20 meters per second from a height of 5 meters. The height h of the ball at time t seconds can be modeled by the equation h=−5t²+20t+5. Determine when the ball will hit the ground.
Solution to Problem 1: Factoring the quadratic equation, we get: x²−7x+10=(x−2)(x−5)=0 Thus, x=2 or x=5.
Solution to Problem 2: To find when the ball hits the ground, set h=0:
0=−5t²+20t+5
Using the quadratic formula,
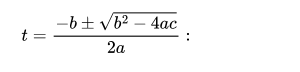


The two types of quadratic formulas are:
The Quadratic Formula for solving equations: x=−b±(b²−4ac)/2a
Three methods to solve quadratic equations are:
Factoring
Using the quadratic formula
Completing the square
The general formula of a quadratic equation is ax²+bx+c=0
No, a quadratic equation can have at most two roots, which might be real or complex, but cannot exceed two distinct solutions.
Text prompt
Add Tone
10 Examples of Public speaking
20 Examples of Gas lighting
What is the standard form of a quadratic equation?
ax^2 + bx + c = 0
ax^2 + b = c
x^2 + b = c
ax + b = c
Which formula is used to find the roots of a quadratic equation?
x = \frac{-b \pm \sqrt{b^2 + 4ac}}{2a}
x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}
x = \frac{-b \pm \sqrt{4ac - b^2}}{2a}
x = \frac{-b \pm \sqrt{b^2 - 4a}}{2c}
What does the discriminant b^2 - 4ac tell us about the roots of a quadratic equation?
The number of real roots
The sum of the roots
The product of the roots
The vertex of the parabola
For the quadratic equation x^2 - 4x + 4 = 0 , what are the roots?
x = 1, x = 4
x = -2, x = -2
x = 2, x = 2
x = -1, x = -4
How can you find the vertex of a parabola given by the quadratic equation y = ax^2 + bx + c ?
\left(-\frac{b}{2a}, -\frac{b^2 - 4ac}{4a}\right)
\left(-\frac{b}{2a}, \frac{b^2 - 4ac}{4a}\right)
\left(-\frac{b}{2a}, \frac{c - b^2}{4a}\right)
\left(\frac{b}{2a}, \frac{c - b^2}{4a}\right)
Which of the following is a perfect square trinomial?
x^2 + 6x + 9
x^2 + 5x + 6
x^2 - 7x + 12
x^2 + 4x + 4
If a quadratic equation has roots 3 and -2 , what is the quadratic equation in its factored form?
(x - 3)(x + 2)
(x + 3)(x - 2)
(x - 3)(x - 2)
(x + 3)(x + 2)
What is the sum of the roots of the quadratic equation x^2 - 8x + 15 = 0 ?
15
-8
8
-15
What is the product of the roots of the quadratic equation 2x^2 - 3x + 1 = 0 ?
\frac{1}{2}
1
\frac{3}{2}
2
What is the axis of symmetry for the quadratic equation y = 4x^2 - 12x + 9 ?
x = 3
x = -3
x = 2
x = -2
Before you leave, take our quick quiz to enhance your learning!

