Laws of Maths

What is Laws of Maths?

The “Laws of Maths” or “Mathematical Laws” refer to fundamental principles that provide the foundational framework for understanding and solving mathematical problems.

1. Arithmetic Laws:

Commutative Law:

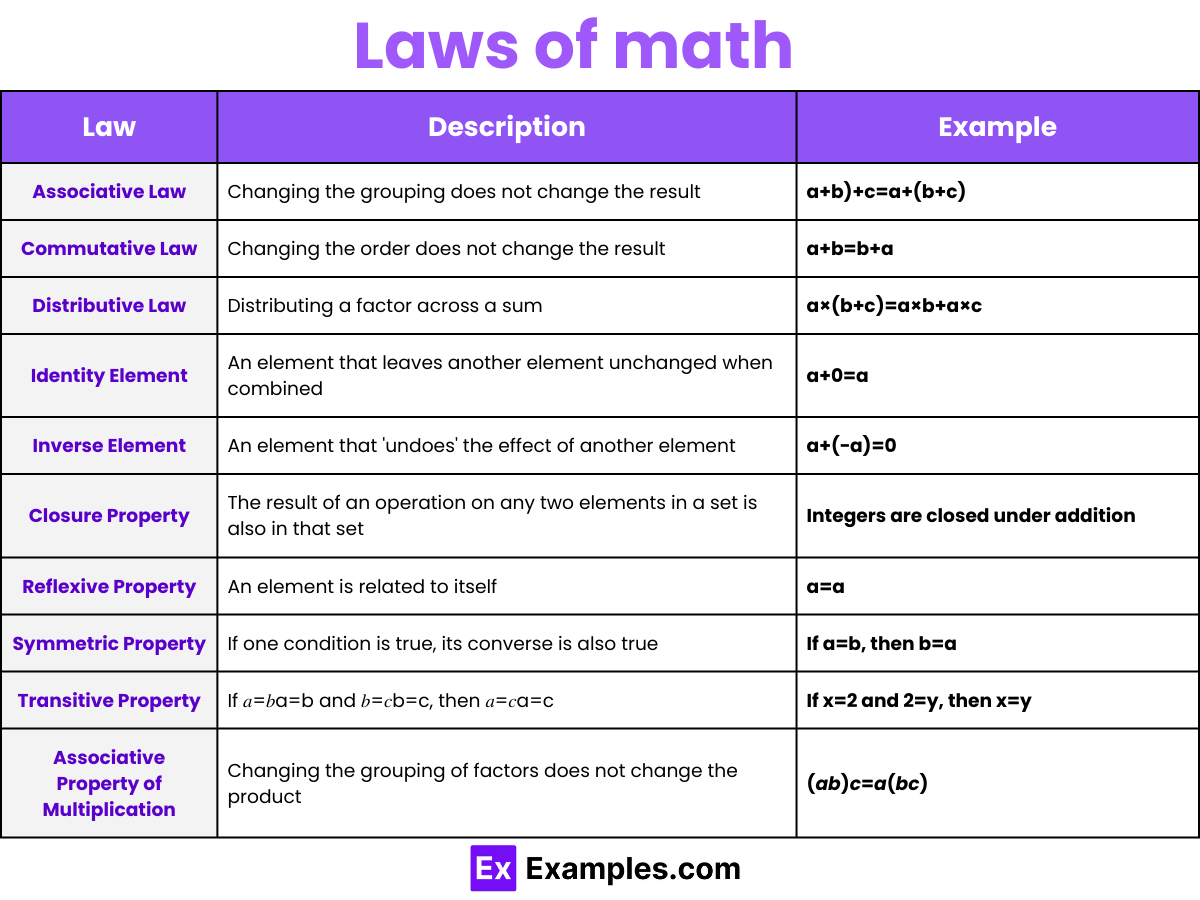
The Commutative Law is a fundamental principle in mathematics that applies to addition and multiplication. It states that the order of numbers in these operations does not affect the result. This law simplifies mathematical calculations and provides consistency. Here’s a detailed look:

Commutative Law of Addition:

• Definition: Changing the order of addends does not change the sum.
  • 𝑎+𝑏=𝑏+𝑎
  • For example, 3+4=4+3 both give 7.

Commutative Law of Multiplication:

• Definition: Changing the order of factors does not change the product.
  • 𝑎×𝑏=𝑏×𝑎
  • For example, 5×2=2×5 both give 10.

Associative Law

The Associative Law is a fundamental principle in mathematics that applies to addition and multiplication. It states that the way in which numbers are grouped in these operations does not affect the result. This law simplifies complex calculations by allowing us to regroup numbers without altering the outcome. Here’s a detailed look:

Associative Law of Addition:

• Definition: Changing the grouping of addends does not change the sum.
  • (𝑎+𝑏)+𝑐=𝑎+(𝑏+𝑐)
  • For example, (1+2)+3=1+(2+3) both give 6.

Associative Law of Multiplication:

• Definition: Changing the grouping of factors does not change the product.
  • (𝑎×𝑏)×𝑐=𝑎×(𝑏×𝑐)
  • For example, (2×3)×4=2×(3×4) both give 24.

Distributive Law:

The Distributive Law is a key mathematical principle that links multiplication and addition. It states that multiplying a number by a sum is the same as multiplying the number by each addend separately and then adding the products together. Here’s a detailed look:

Distributive Law:

• Definition: The law states that for any numbers 𝑎,𝑏,𝑐a,b,c:
  • 𝑎(𝑏+𝑐)=𝑎𝑏+𝑎𝑐
  • This means that 𝑎a multiplies both 𝑏 and 𝑐 individually, and the products are then summed.

Example:

• Let’s consider 3(2+4)
  • Step 1: Apply the Distributive Law: 3(2+4)=3×2+3×4
  • Step 2: Multiply each number individually:
    • 3×2=6
    • 3×4=12
  • Step 3: Sum the results: 6+12=18

2. Algebraic Laws:

Algebraic Laws are fundamental principles that provide a structured framework for handling algebraic expressions and equation. These laws simplify and guide calculations in algebra, ensuring consistent and reliable results. Here are key algebraic laws:

1. Zero Product Law:

Definition: If the product of two numbers is zero, then at least one of the numbers must be zero.

•  𝑎𝑏=0  ⟹ 𝑎=0 or 𝑏=0
• For example, if (𝑥−3)(𝑥+2)=0, then either 𝑥−3=0 or 𝑥+2=0, leading to solutions 𝑥=3 or 𝑥=−2.

2. Laws of Exponents:

Product of Powers: Multiplying two powers with the same base adds their exponents.

• (𝑎ᵐ)ⁿ=𝑎ᵐ×𝑛(aᵐ)ⁿ=aᵐˣⁿ
• For example, (2²)³=2⁶.

3. Laws of Logarithms:

Logarithmic Identity: The logarithm of a number raised to an exponent is the exponent times the logarithm of the base.

log⁡𝑏(𝑎ⁿ)=𝑛⋅log⁡𝑏(𝑎)

Logarithmic Addition: The logarithm of a product is the sum of the logarithms of its factors.

log⁡𝑏(𝑎𝑏)=log⁡𝑏(𝑎)+log⁡𝑏(𝑏)

3. Laws of Logic:

Laws of Logic are fundamental principles that provide a framework for reasoning and constructing valid arguments. They form the foundation for logical thinking and help ensure that arguments and statements are coherent and consistent. Here are key laws of logic:

1. Law of Identity:

• Definition: An object or statement is equal to itself.
  • 𝑎=𝑎
• Application: This law affirms that any entity or proposition remains consistent, reinforcing coherent reasoning.

2. Law of Non-Contradiction:

• Definition: A statement cannot be both true and false simultaneously.
  • ¬(𝑎 and ¬𝑎)
  • For example, if a proposition states, “It is raining,” it cannot simultaneously be true that “It is not raining.”
• Application: This law prevents contradictory reasoning, ensuring clarity and consistency in arguments.

3. Law of Excluded Middle:

• Definition: A statement is either true or false, with no middle ground.
  • 𝑎 or ¬𝑎
• Application: This law ensures binary logic, which is fundamental to many areas, including computer science and mathematics.

4. Geometric Laws:

1. Pythagorean Theorem:

• Definition: In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the two other sides.
  • 𝑎²+𝑏²=𝑐²For example, if a triangle has legs of length 3 and 4, then the hypotenuse is 32+42=25=5²

2. Laws of Angles:

• Interior Angles of a Triangle: The interior angles of a triangle always sum to 180 degrees.
  • 𝛼+𝛽+𝛾=180⁰
• Supplementary Angles: Two angles that form a straight line (180 degrees) are supplementary.
  • For example, if angle 𝐴 is 120 degrees, then angle 𝐵 is 60 degrees to make a straight line.

3. Circle Theorems:

• Central Angle Theorem: An angle at the center of a circle formed by two radii is twice the inscribed angle on the circumference subtended by the same arc.
• Tangent-Secant Theorem: If a tangent and secant intersect at a point outside a circle, then the square of the tangent segment is equal to the product of the secant segments.

4. Law of Cosines:

• Definition: For any triangle with sides 𝑎,𝑏,𝑐 and opposite angles 𝐴,𝐵,𝐶 respectively:
  • 𝑐2=𝑎2+𝑏2−2𝑎𝑏cos⁡(𝐶)
• Application: This law generalizes the Pythagorean Theorem for non-right triangles.

Tips for using these laws of Math

1. Break Down Problems: Use the Commutative, Associative, and Distributive Laws to break down complex equations into simpler steps, allowing for easier manipulation and solving.
2. Apply Logical Consistency: The Laws of Logic ensure that your statements and arguments remain coherent. Apply these consistently when constructing mathematical proofs or solving problems.
3. Use Geometric Relationships: The Pythagorean Theorem and other geometric laws provide tools for understanding shapes and spatial relationships. Leverage these to simplify and solve geometry problems effectively.
4. Factoring Quadratics: The Zero Product Law is essential when solving quadratic equations. Factor them into linear expressions, and apply the law to find solutions.
5. Practice Regularly: Strengthen your understanding by applying these laws in various contexts, from arithmetic to algebra and geometry, solidifying your grasp and expanding your problem-solving skills

Practice Problems

Question 1:

Explain the Commutative Law with examples for both addition and multiplication.

Answer: The Commutative Law states that the order of numbers does not affect the result for addition or multiplication.

• Commutative Law of Addition: 𝑎+𝑏=𝑏+𝑎
  • Example: 3+5=5+3both yield 8.
• Commutative Law of Multiplication: 𝑎×𝑏=𝑏×𝑎
  • Example: 4×6=6×4 both yield 24.

This law simplifies calculations by allowing flexibility in the order of operations, providing consistency and reducing the steps required for arithmetic tasks.

Question 2:

Define the Distributive Law and demonstrate how it simplifies the expression 4(3+2)4(3+2).

Answer: The Distributive Law states that multiplying a number by a sum is equivalent to multiplying the number by each addend separately and then summing the products: 𝑎(𝑏+𝑐)=𝑎𝑏+𝑎𝑐a(b+c)=ab+ac.

Applying this law to 4(3+2)

• 4(3+2)=4×3+4×2
• =12+8
• =20

Thus, the Distributive Law simplifies expressions by breaking them down into manageable steps, allowing easy manipulation and solving of algebraic equations.

FAQs

What are Mathematical Laws?

Mathematical laws are foundational principles that define relationships and operations between numbers, equations, and logical statements. They provide a consistent framework for solving problems, simplifying calculations, and understanding complex mathematical concepts, ensuring coherent and reliable results in arithmetic, algebra, geometry, and beyond.

What are the Three Laws of Math?

The three primary laws of math include:

• Commutative Law: Order of addition or multiplication does not affect the result.
• Associative Law: Grouping of numbers does not change the sum or product.
• Distributive Law: Multiplication distributes over addition.

What are the 4 Rules of Math?

The four rules of math refer to basic arithmetic operation:

1. Addition: Combining numbers to form a sum.
2. Subtraction: Finding the difference between numbers.
3. Multiplication: Repeated addition of a number.
4. Division: Splitting a number into equal parts.

What is Rule 5 in Math?

Rule 5 in math can refer to a specific rule related to exponents:

• Laws of Exponents: For any number 𝑎a and powers 𝑚m and 𝑛n:
  • (𝑎ᵐ)ⁿ=𝑎ᵐ×𝑛(aᵐ)ⁿ=aᵐˣⁿ This generalizes to many mathematical expressions and ensures consistent calculations.