What is 12 × 15?
160
170
180
190

Multiplication is a fundamental mathematical operation, representing the process of adding a number to itself a certain number of times. It’s not just a building block for math education but a critical tool in daily life and advanced science. Multiplication stands as one of the primary mathematical operations, sharing this core status with addition, subtraction, and division.This guide unveils its intricacies, applications, and tips for mastery, making multiplication accessible to learners at all levels
What is Multiplication?
Multiplication stands as one of the primary mathematical operations, sharing this core status with addition, subtraction, and division. Essentially, to multiply means to add together equal-sized groups repeatedly. This operation serves as a fundamental building block in mathematics, facilitating the calculation of numerous equal parts or quantities in a streamlined manner.

The multiplication symbol, denoted as “×,” serves as the mathematical operator indicating multiplication between two numbers or expressions. It is a cross-shaped sign that signifies the operation of taking one number and adding it to itself a certain number of times, as determined by the second number. For example, in the expression “4 × 3,” the “×” symbol instructs us to multiply 4 by 3, resulting in 12. This symbol is universally recognized in mathematics to represent the concept of multiplication.
The formula for multiplication is straightforward, involving two numbers or variables that are multiplied together to find their product. Represented symbolically, it is:
Product=a×b
Product = Multiplicand × Multiplier
Where:
Example:
8(multiplicand) × 5 (multiplier) = 40 (product)
Identify the Numbers: Choose the two numbers you want to multiply. This method is easiest with single-digit numbers, but it can also apply to specific cases of larger numbers.
Multiply Each Pair of Digits: If you’re dealing with single-digit numbers, simply multiply them together. For example, 3×4=12. If your numbers are larger but carefully chosen (or the circumstances work out such that) no single multiplication step results in a number greater than 9, you can apply the same principle.
Write the Product: Since there’s no need to regroup (or carry), you can directly write down the answer obtained from your multiplication.
Multiplication using a number line is a visual method that helps illustrate the concept of multiplication as repeated addition. This technique is especially useful for teaching young learners or those new to the concept of multiplication. Here’s how to perform multiplication using a number line:
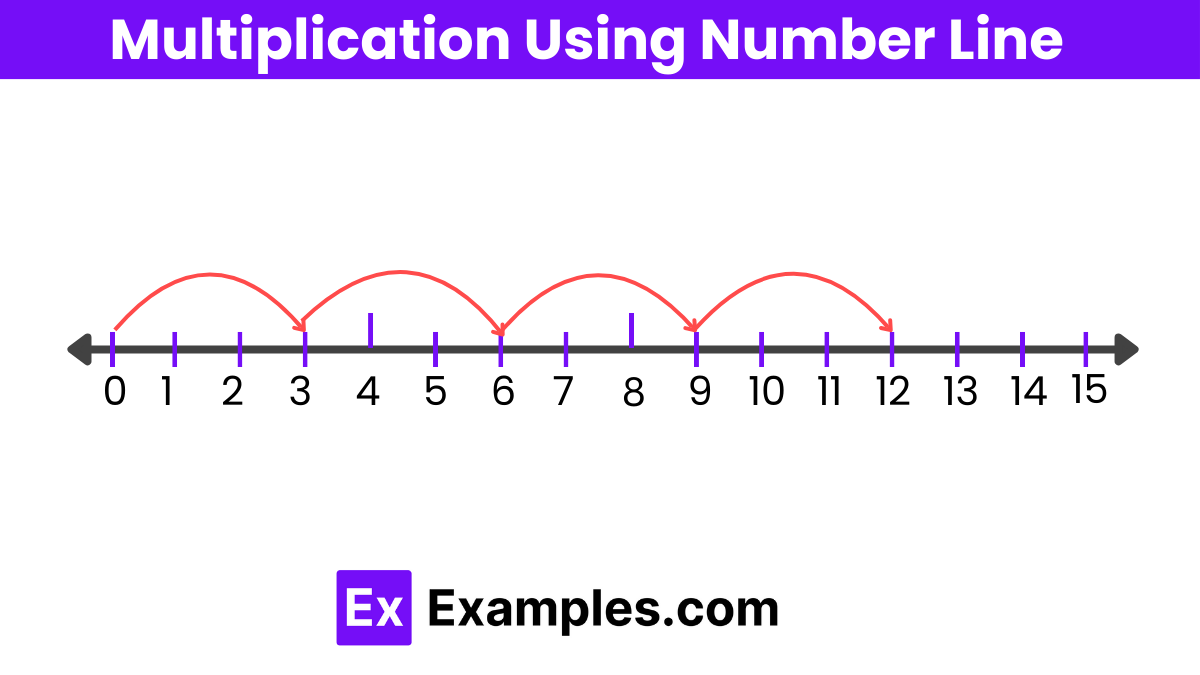
Make Hops on the Number Line: Start at zero. For each multiplication operation, make hops equal to the value of the multiplicand. Each hop should span a number of spaces on the number line equal to the multiplicand.

Question: A landscaper plants 8 rows of flowers in a garden. Each row contains 9 flowers. How many flowers are there in total?
Answer: To find the total number of flowers, multiply the number of flowers per row by the number of rows: 8 rows×9 flowers/row=72 flowers Total Flowers: 72
Question: A factory produces 250 car parts each day. How many car parts are produced in 20 days?
Answer: Multiply the number of car parts produced each day by the number of days: 250 parts/day×20 days=5000 parts Total Parts Produced: 5000
Question: Each box of tea bags contains 15 tea bags. If a store sells 36 boxes, how many tea bags were sold?
Answer: Multiply the number of tea bags per box by the number of boxes sold: 15 tea bags/box×36 boxes=540 tea bags Total Tea Bags Sold: 540
Question: A parking lot has 45 spaces. On a particular day, if 32 cars are parked in each space, how many cars are in the parking lot?
Answer: Multiply the number of spaces by the number of cars per space: 45 spaces×32 cars/space=1440 cars Total Cars Parked: 1440
Question: A concert hall has 24 rows of seats. Each row has 42 seats. How many seats are in the concert hall?
Answer: Multiply the number of rows by the number of seats per row: 24 rows×42 seats/row=1008 seats Total Seats in Concert Hall: 1008
Question: A school cafeteria serves lunch to 18 classes each day. If each class has 26 students, how many students in total are served lunch?
Answer: Multiply the number of classes by the number of students per class: 18 classes×26 students/class=468 students Total Students Served: 468
The terms multiplicand and multiplier are factors in a multiplication equation. The multiplicand is the number being multiplied, while the multiplier is the quantity by which the multiplicand is multiplied. For instance, in 4×3, 4 is the multiplicand, and 3 is the multiplier, yielding a product of 12.
To explain multiplication to a child, describe it as repeated addition. For example, if you have 3 groups of 4 apples, multiplication tells you the total number of apples. You simply add the number in each group together: 4+4+4=12 apples. This shows that 3×4=12.
For kids, “multiply” means combining equal groups to find out how many items there are altogether. It is like adding the same number several times. For example, if you have 5 groups of 2 cookies, multiplying 5×25×2 tells you that there are 10 cookies in total.
Multiplier math involves using one number (the multiplier) to increase another number (the multiplicand) repeatedly. The process is simple: multiply the multiplicand by the multiplier to get the product. For instance, multiplying 6 (multiplicand) by 4 (multiplier) means adding 6 to itself 4 times, resulting in 24.
In Grade 2, multiplication is introduced as a method for quick addition of equal groups. Students learn to interpret multiplication as repeated addition, such as seeing 5×35×3 as adding three 5s (5+5+5). This foundational concept helps them understand how multiplication facilitates efficient counting and problem-solving.
Text prompt
Add Tone
10 Examples of Public speaking
20 Examples of Gas lighting
What is 12 × 15?
160
170
180
190
Calculate the product of 23 and 8.
184
186
188
190
What is the result of multiplying 9 by 16?
132
144
156
168
Find the product of 7 and 13.
81
85
91
95
What is 14 multiplied by 12?
158
168
178
188
Calculate 17 × 19.
313
323
333
343
What is the product of 25 and 11?
265
275
285
290
Find the result of multiplying 6 by 24.
134
144
154
164
What is 32 multiplied by 5?
140
150
160
170
Calculate the product of 13 and 13.
159
169
179
189
Before you leave, take our quick quiz to enhance your learning!

