Addition
Addition, the fundamental building block of arithmetic, involves combining two or more numbers to find their total. This guide aims to simplify addition through engaging examples and practical tips, making it accessible to learners of all levels. Whether you’re teaching basic single-digit addition or exploring more complex problems, our resource is packed with strategies to enhance understanding and foster a love for mathematics. By mastering addition, students lay the groundwork for future success in math, developing skills crucial for problem-solving and logical thinking.
What is Addition?
Addition is a basic arithmetic operation that combines two or more quantities to find their total sum. It’s the first and most essential concept introduced in mathematics, serving as the foundation for more advanced topics. Understanding addition is crucial for everyday tasks, from simple calculations to complex financial planning. It involves adding together numbers or amounts to get a total, symbolized by the plus sign (+). For example, adding 2 and 3 results in a sum of 5 (2 + 3 = 5). Through addition, students learn to count, measure, and analyze data, making it a vital skill in both academic and real-world settings.
Addition Symbol with terms
The addition symbol, denoted as “+”, is a mathematical sign used to indicate the operation of adding two or more quantities. It is one of the most recognizable and widely used symbols in mathematics, appearing in everything from elementary arithmetic to complex algebraic equations.Whenever we perform significantly large numbers or more items, then we can use the sigma symbol (∑).
- Addend: A number involved in an addition operation.
- Sum: The result of adding two or more addends.
- Plus Sign (+): The symbol that denotes addition.
- Equals Sign (=): Indicates that the values on either side are equal.
The Role of the Plus Sign in Mathematics
- Basic Arithmetic: In its most basic form, the plus sign is used to add numbers, as in “3 + 4 = 7.” It signifies the operation of combining quantities to find their total.
- Algebra: In algebra, the plus sign is used to add variables and constants, as well as to indicate positive numbers.
- Equations and Inequalities: The symbol appears in equations and inequalities to denote addition on either side of the equation or inequality.Vector Addition: In physics and engineering, the plus sign is used to denote vector addition, where it represents the sum of vectors in terms of magnitude and direction.
Parts of Addition
The components of an addition operation are detailed in the following figure:
Addition Table
The following figure highlights the method of adding simple numbers, facilitating the creation the individual addition tables for numbers ranging from 1 to 10.
Properties of Addition
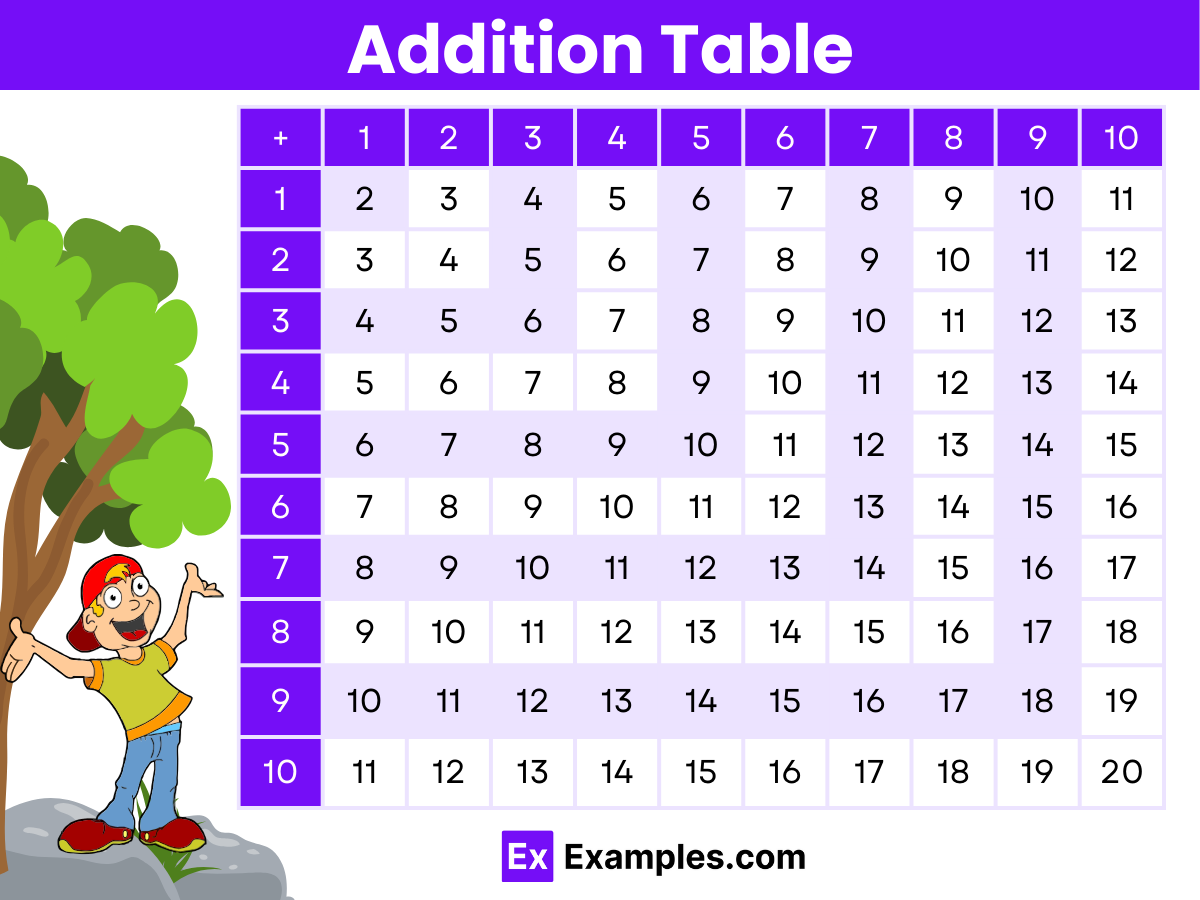
Addition, a fundamental operation in mathematics, is governed by several key properties that help us understand how numbers interact when they are combined. These properties are not only crucial for basic arithmetic but also play a significant role in more advanced mathematical concepts and operations. Let’s delve into these properties:
Commutative Property of Addition
The Commutative Property of Addition states that changing the order of the addends does not affect the sum. This means that if you are adding two numbers, it doesn’t matter in which order you add them; the result will always be the same.
- Example: 5 + 3 = 3 + 5
Associative Property of Addition
The Associative Property of Addition indicates that when adding three or more numbers, the way the numbers are grouped (or associated) does not change the sum. This property allows us to add or group numbers in any order, which is particularly useful for simplifying calculations.
- Example: (4 + 2) + 3 = 4 + (2 + 3)
Identity Property of Addition
The Identity Property of Addition describes how adding zero to any number leaves the number unchanged. Zero is known as the “additive identity” because it is the only number that can be added to another number without changing its value.
- Example: 7 + 0 = 7
Distributive Property of Addition over Multiplication
The Distributive Property connects addition and multiplication. It states that multiplying a number by a sum is the same as multiplying each addend by the number and then adding the products. This property is essential for simplifying expressions and solving equations.
- Example: 3 * (4 + 5) = (3 * 4) + (3 * 5)
Zero Property of Addition
While not as commonly listed among the basic properties, the Zero Property of Addition emphasizes the unique role of 0 in the addition operation. It complements the Identity Property by highlighting 0’s ability to not alter the value of another number when added together.
- Example: Any number + 0 = That same number
Methods of Addition
There are various strategies and methods to add numbers in maths and they are:
- Addition Using Counting
- Addition on Number Line
- Addition with Regrouping
- Addition without Regrouping
Addition Using Counting
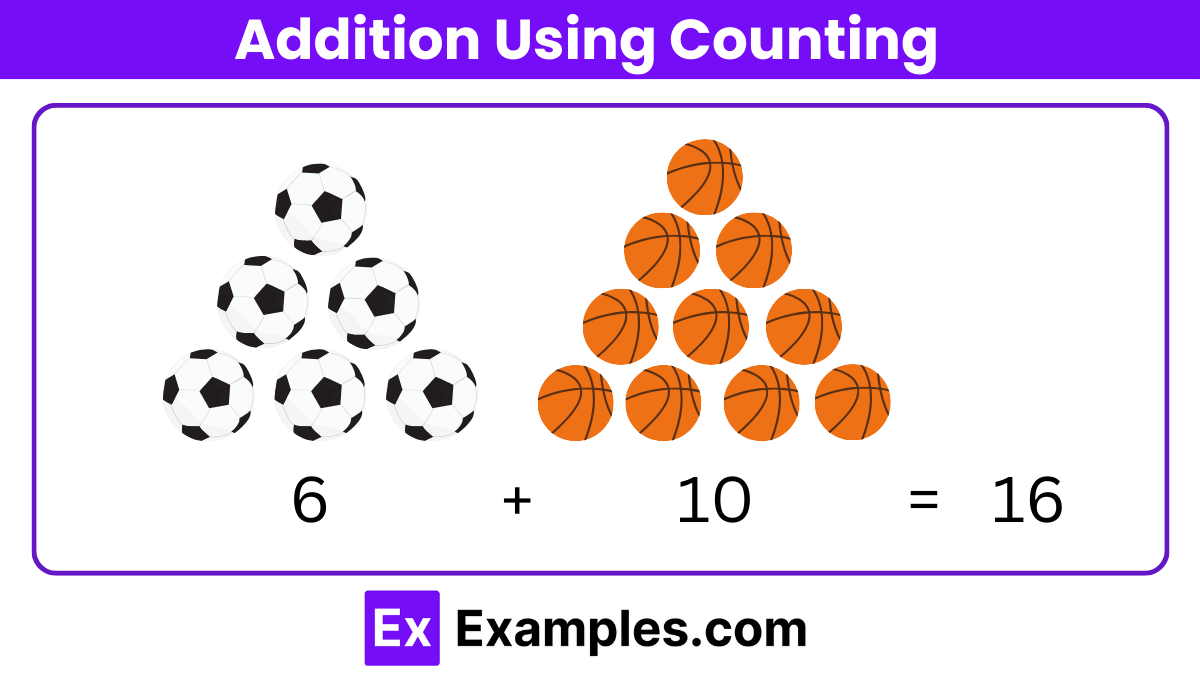
In the figure given below, 6 yellow balls and 10 purple balls are given. By counting the number of each coloure
Addition on Number Line
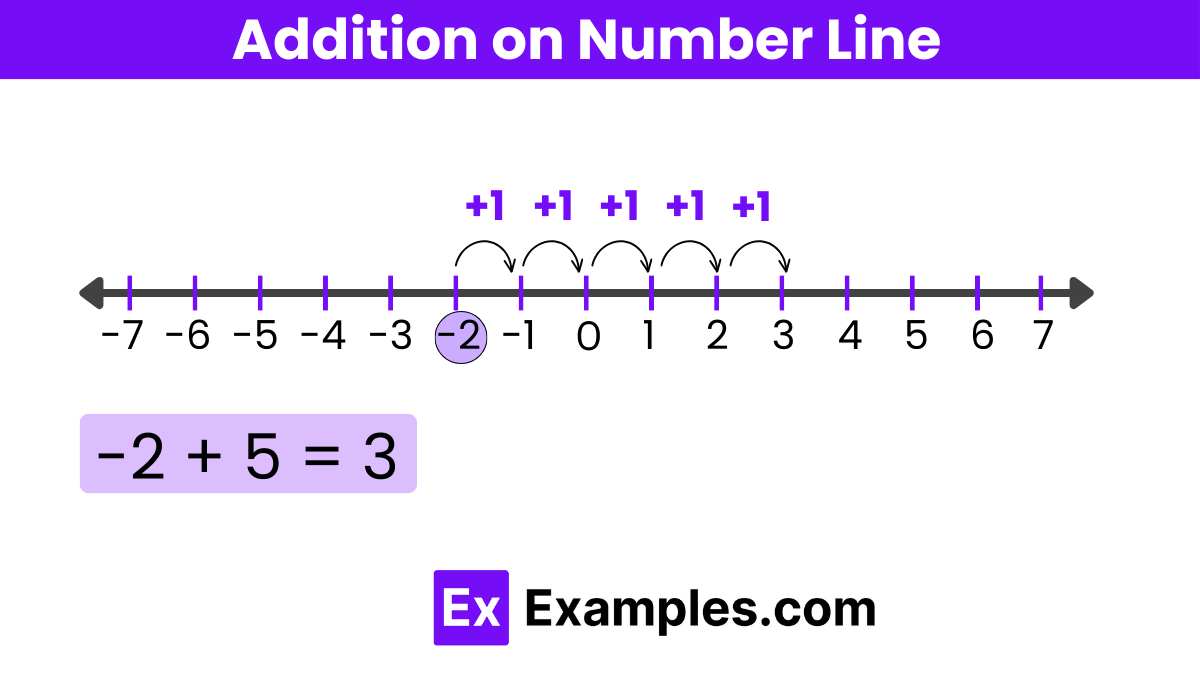
A number line is a visual representation of numbers on a straight line, where each point on the line corresponds to a number. It serves as a powerful tool for understanding and performing various mathematical operations, including addition. Addition on a number line involves moving to the right of a given point to represent an increase in value.
- Start at the First Number: Identify the first number in the addition equation and locate its position on the number line. This point serves as your starting position.
- Move Right for the Second Number: Determine the value of the second number (the addend) you are adding to the first. From the starting point on the number line, move to the right by a number of units equal to the value of the second number. The direction to the right indicates an increase in value.
- Find the Sum: The point where you land after moving to the right represents the sum of the two numbers. This final position on the number line shows the result of the addition operation.
Addition with Regrouping
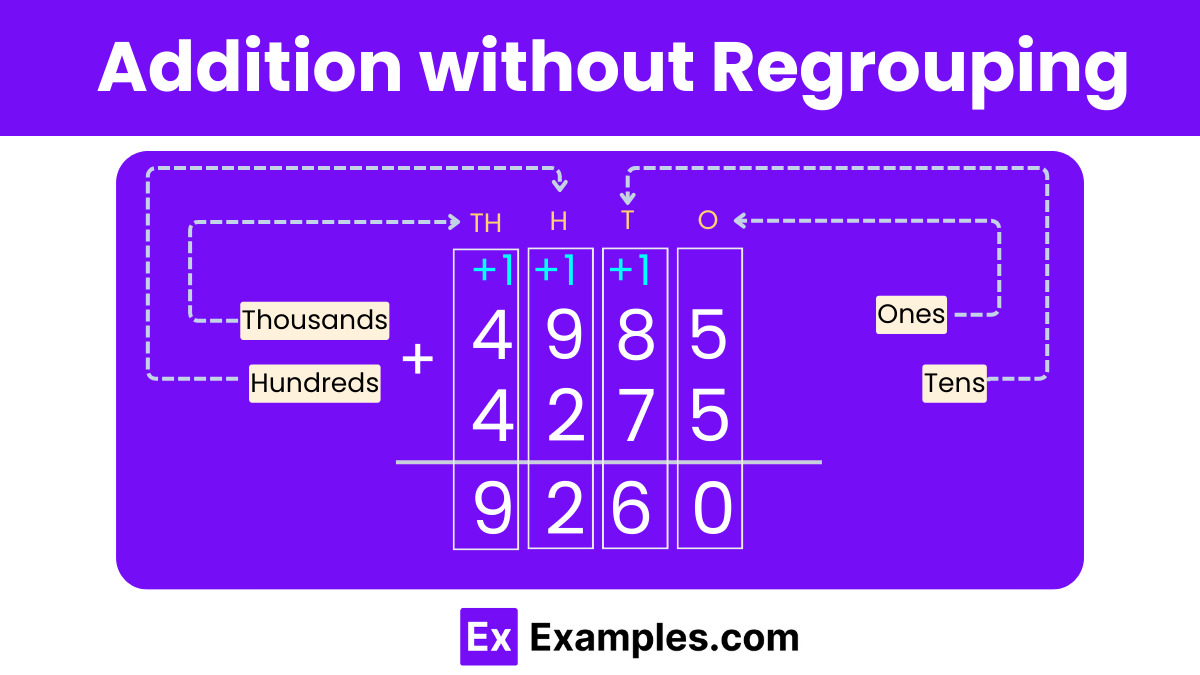
As described previously, adding single-digit numbers on a number line is quite straightforward. However, when it comes to adding numbers that consist of two or more digits, the strategy involves a technique known as regrouping. In mathematics, regrouping is essentially the method of rearranging digits according to their place values—such as tens, hundreds, or thousands—to simplify operations like addition and subtraction when dealing with multi-digit numbers. This technique ensures that digits of similar place values are grouped together, facilitating easier calculation and combination of these larger numbers
Let’s have a look at the example given below:
Example: Add two numbers 49 and 52.
Solution:
When adding digits in the ones column, starting from the lower number and moving upwards, we encounter the sum of 9 + 2, which equals 11.
Given that only a single digit up to 9 can occupy the ones place, the entirety of 13 cannot be placed there. Therefore, we position the ones digit (1) in the ones column and carry over the remaining digit (1 from 11) to the next higher place value, which is the tens column.
The next step involves adding the digits in the tens column: 4 + 5. It’s crucial not to overlook the addition of the carried over digit, resulting in 4 + 5 + 1.
The sum here is 10, which we then write in the tens column, culminating in an overall total of 101.
This method of addition, involving carrying over or regrouping, applies equally to numbers with three or more digits.
Moreover, beyond number lines and regrouping, there are alternative methods for adding numbers, such as using finger counting for lesser sums.
Additionally, for further practice, consider utilizing addition worksheets available through various resources
When adding digits in the ones column, starting from the lower number and moving upwards, we encounter the sum of 9 + 2, which equals 11.
Given that only a single digit up to 9 can occupy the ones place, the entirety of 13 cannot be placed there. Therefore, we position the ones digit (1) in the ones column and carry over the remaining digit (1 from 11) to the next higher place value, which is the tens column.
The next step involves adding the digits in the tens column: 4 + 5. It’s crucial not to overlook the addition of the carried over digit, resulting in 4 + 5 + 1.
The sum here is 10, which we then write in the tens column, culminating in an overall total of 101.
This method of addition, involving carrying over or regrouping, applies equally to numbers with three or more digits.
Moreover, beyond number lines and regrouping, there are alternative methods for adding numbers, such as using finger counting for lesser sums.
Additionally, for further practice, consider utilizing addition worksheets available through various resources
Addition without Regrouping
When adding numbers and the total in any column exceeds 9, we employ regrouping, dividing the sum into tens and ones. The digit representing tens is carried over to the next left column, while the digit in the ones place is recorded in the current column. This process, essentially, involves noting the ‘ones place digit’ in its respective column and shifting the ‘tens place digit’ to the column immediately to its left. To better grasp the concept of adding numbers through regrouping, let’s explore it through an illustrative example.
Example: Add 4985 and 4275.
Solution: Let us follow the given steps and try to relate them with the following figure.
- Step 1: Start with the digits in ones place. (5 + 5 = 10). Here the sum is 10. The tens digit of the sum, that is, 1, will be carried to the preceding column.
- Step 2: Add the digits in the tens column along with the carryover 1. This means, 1 (carry-over) + 8 + 7 = 16. Here the sum is 16. The tens digit of the sum, that is, 1, will be carried to the hundreds column.
- Step 3: Now, add the digits in the hundreds place along with the carryover digit 1. This means, 1 (carry-over) + 9 + 2 = 12. Here the sum is 12. The tens digit of the sum, that is, 1, will be carried to the thousands column.
- Step 4: Now, add the digits in the thousands place along with the carryover digit 1, that is, 1 (carry-over) + 4+ 4= 9
- Step 5: Therefore, the sum of 4985 + 4275= 9260
Tricks of Addition Using Fingers
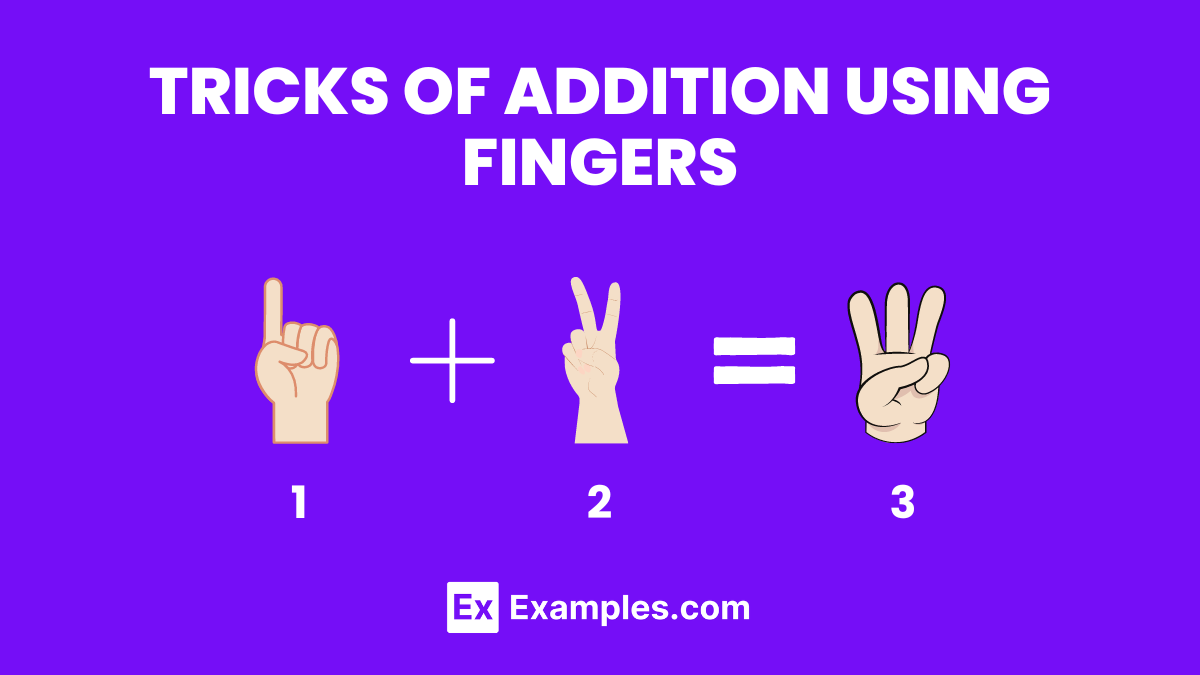
Using fingers to add numbers is a practical and visual method, especially effective for young learners or when a calculator isn’t handy.
Steps to use fingers for addition:
1) Assign each finger a value (1 through 10).
2) For single-digit addition, raise the number of fingers corresponding to each number being added.
3) Count the total number of raised fingers for the sum.
Example: For 4 + 3, raise four fingers on one hand and three on the other, totaling seven fingers raised, which equals 7. This method is particularly useful for quick calculations and reinforcing the concept of addition for beginners.
Rules for Addition
Understanding the basic rules of addition is crucial for both teachers aiming to impart this knowledge and students looking to enhance their mathematical skills. Addition is a fundamental arithmetic operation that combines two or more numbers to form a total sum. Here are some key points to keep in mind:
- Start with smaller numbers: Begin by adding single-digit numbers to grasp the concept.
- Use visual aids: Counters, blocks, or drawings can help visualize the process.
- Move left to right: Add numbers from the rightmost digit (units) and move towards the left (tens, hundreds).
- Carry over when necessary: If the sum of any column exceeds nine, carry over to the next column.
- Practice regularly: Consistent practice with varied problems enhances understanding and speed.
Addition of One-Digit Numbers
Adding one-digit numbers is the foundation of arithmetic. This skill is essential for young learners as it sets the stage for more complex calculations. Here are some strategies to make the process engaging and effective:
- Use counting objects: Utilize beads, blocks, or fingers to represent numbers visually.
- Memorize basic facts: Encourage memorization of sums up to 10 to speed up calculation.
- Interactive games: Incorporate educational games that require quick addition to make learning fun.
- Repeat practice: Consistent repetition ensures mastery of these fundamental sums.
- Real-life examples: Use examples like adding apples or books to make the concept relatable.
Example: 5 + 3 = 8. This simple addition can be visualized by counting five objects, then adding three more, totaling eight.
Addition for Two-Digit Numbers
Adding two-digit numbers introduces the concept of carrying over, a crucial step in understanding larger calculations. Here’s how to approach it:
- Align the numbers vertically: Ensure the units and tens digits are in the correct columns.
- Add the units first: Start with the rightmost column and move left.
- Carry over: If the sum of the units column is 10 or more, carry over to the tens column.
- Add the tens: Include any carried over amount in this sum.
- Use place value understanding: Reinforce the concept of tens and units during the process.
Example: 34 + 27 = 61. Add the units column (4 + 7 = 11, carry the 1), then the tens column (3 + 2 + 1 = 6).
Addition for Three-Digit Numbers
As students progress, adding three-digit numbers further solidifies their arithmetic foundation. Here’s a structured approach:
- Line up the numbers: Ensure hundreds, tens, and units are correctly aligned.
- Start from the right: Begin with the units column, then move to tens, and finally hundreds.
- Carry over: Apply the carry-over principle when sums exceed nine.
- Reinforce place value: Continuously emphasize the value of each digit according to its position.
- Use real-life scenarios: Integrate examples like adding money or distances to make the concept tangible.
Example: 256 + 378 = 634. Start with the units (6 + 8 = 14, carry 1), move to tens (5 + 7 + 1 = 13, carry 1), and finish with hundreds (2 + 3 + 1 = 6).
This guide offers a structured approach to teaching addition, catering to the needs of educators and learners aiming for a comprehensive understanding of basic arithmetic operations.
Word Problems on Addition
Word problems in mathematics help students apply their understanding of mathematical concepts to real-world situations. Addition word problems often involve scenarios where quantities are combined, requiring the solver to perform addition to find the solution. Below are some examples of addition word problems across different contexts.
Problem 1: Fruit Market
Samantha went to the fruit market to buy apples and oranges. She bought 15 apples and 22 oranges. How many pieces of fruit did Samantha buy in total?
Solution: To find the total number of fruits Samantha bought, add the number of apples to the number of oranges: 15 apples + 22 oranges = 37 fruits. Samantha bought a total of 37 fruits.
Problem 2: Saving Money
Lucas has been saving money for a new bicycle. At the start of the month, he had $75 in his savings. By the end of the month, he managed to save an additional $50. How much money does Lucas have now in his savings?
Solution: To find out how much money Lucas has now, add his initial savings to the amount he saved this month: $75 + $50 = $125. Lucas now has $125 in his savings.
Problem 3: Library Books
A school library had 328 books in its collection. This week, the librarian added 47 new books to the collection. How many books are there in the library now?
Solution: To find the total number of books in the library now, add the number of new books to the existing collection: 328 books + 47 books = 375 books. The library now has a total of 375 books.
Problem 4: Birthday Party Invitations
For her birthday party, Maria sent invitations to 12 of her friends from school and 8 of her cousins. How many invitations did Maria send out in total?
Solution: To determine the total number of invitations Maria sent out, add the number of friends to the number of cousins she invited: 12 friends + 8 cousins = 20 invitations. Maria sent out a total of 20 invitations.
Problem 5: Classroom Chairs
A classroom had 24 chairs. To accommodate more students, the school provided an additional 16 chairs for the classroom. How many chairs are there in the classroom now?
Solution: To find the current number of chairs in the classroom, add the additional chairs to the original number: 24 chairs + 16 chairs = 40 chairs. The classroom now has a total of 40 chairs.
FAQs
What Is the Addition Equation?
An addition equation is a mathematical statement that represents the sum of two or more numbers, using the plus sign (+) and equals sign (=), such as 2 + 3 = 5. It illustrates how when numbers are combined, they form a total.
What Is Addition Class 5?
In Class 5, addition involves more complex problems, including large numbers, decimals, and fractions. Students learn to apply addition in varied contexts, enhancing their problem-solving and numerical skills.
Is Addition a Formula?
Addition itself is not a formula but a basic arithmetic operation. It follows the simple principle of combining numbers to get a sum, without a specific formulaic structure like those seen in algebra or calculus.
How Do You Solve by Addition Method?
To solve by the addition method, especially in systems of equations, align the equations and add them together. This method aims to eliminate one variable, making it easier to solve for the remaining variable.
How to Add Fractions?
To add fractions, ensure they have a common denominator. If they do not, find the least common denominator, adjust the fractions accordingly, and then add the numerators. The denominator remains the same
Understanding and mastering addition is crucial for students, laying the groundwork for all future mathematical learning. By employing diverse teaching strategies and resources, educators can foster a deep, practical understanding of addition, equipping students with essential skills for academic success and everyday life.
Share :
