Least squares

What is Least Square Method?

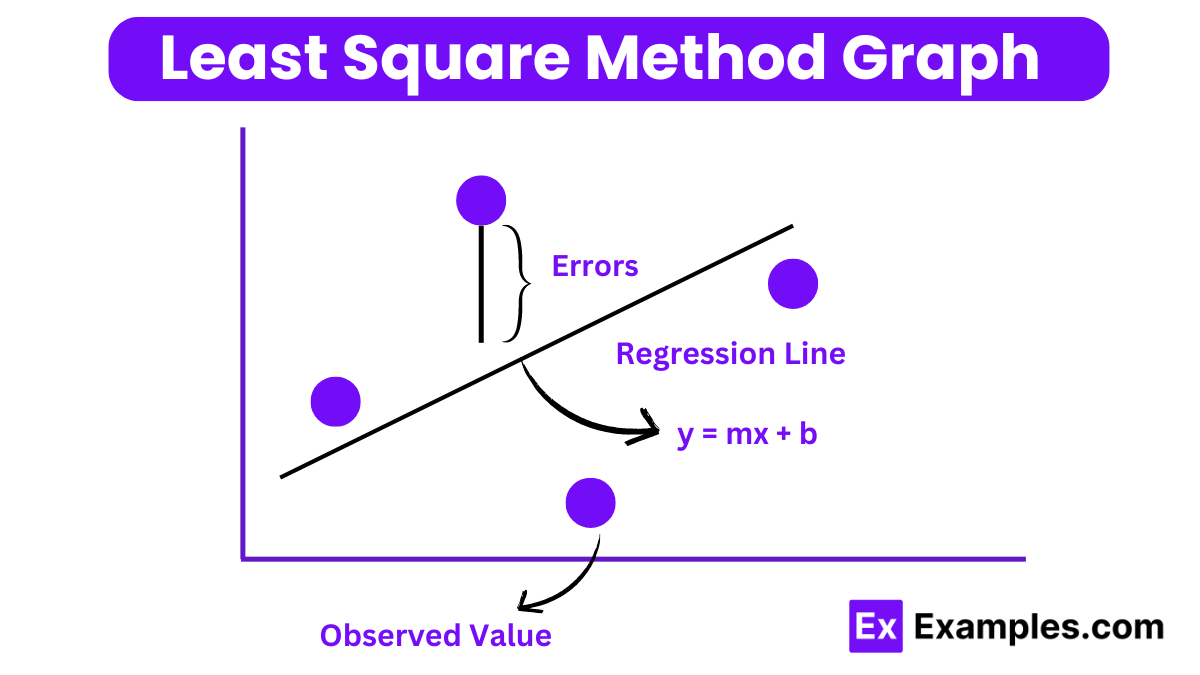
The Least Square Method is a statistical technique used to determine the best fit line for a set of data points by minimizing the sum of the squares of the vertical deviations (residuals) from each data point to the line. This approach is widely used in regression analysis to estimate the parameters of a linear model, aiming to reduce the difference between the observed values and the values predicted by the model. It is applicable in various fields for fitting a model to data, thereby enabling predictions and inferences about the relationships between variables

Least Square Method Formula

The formula for the Least Square Method, particularly in the context of fitting a linear regression line y=mx+b to a set of data points, involves calculating the slope (m) and the y-intercept (b) of the line that minimizes the sum of squared differences between the observed values and the values predicted by the line. The formulas are as follows:

Slope(m):

m=[n(∑xy)−(∑x)(∑y)​]/[n(∑x²)−(∑x)²]

Y-intercept:

b=[(∑y)−m(∑x)]/n

Where:

• n is the number of data points,
• ∑x is the sum of all x-values,
• ∑y is the sum of all y-values,
• ∑xy is the sum of the product of each pair of x and y values, and
• ∑x² is the sum of the squares of x-values.

Least Square Method Graph

In linear regression, the line of best fit is depicted as a straight line in the diagram below:

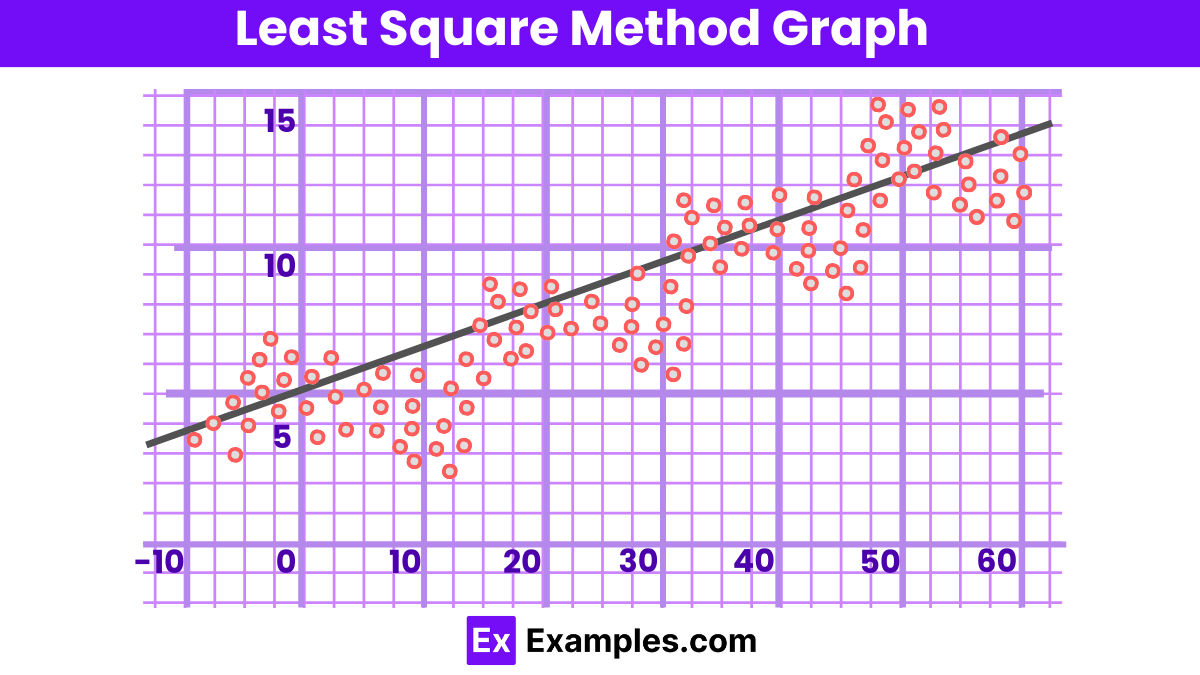
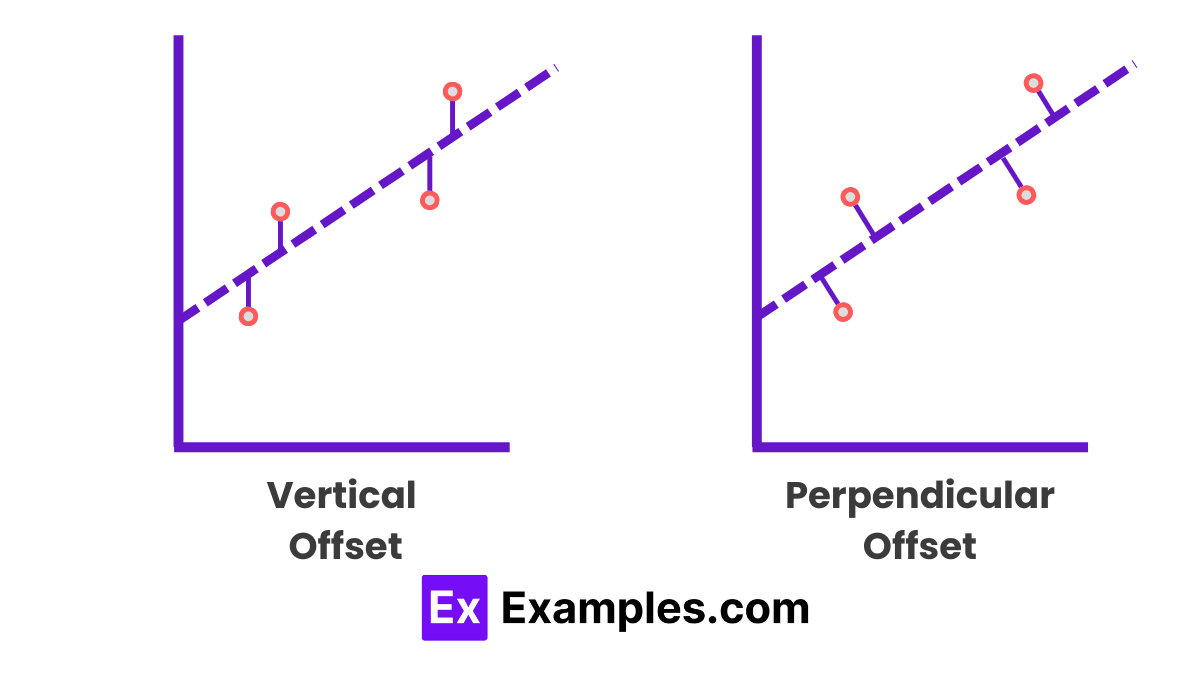
To minimize the given data points, the method involves reducing the residuals or offsets of each point from the line, typically using vertical offsets for surface, polynomial, and hyperplane problems, and perpendicular offsets in standard practice.

Limitations of the Least-Square Method

The least-square method, while widely used for data analysis and prediction, comes with its set of limitations:

• Sensitivity to Outliers: The least squares method is highly sensitive to outliers. Since it minimizes the sum of the squares of the residuals, even a single outlier can significantly skew the results by disproportionately influencing the best-fit line.
• Assumption of Linearity: This method assumes a linear relationship between the independent and dependent variables. It may not provide accurate models or predictions for data that inherently exhibits a non-linear relationship.
• Homoscedasticity Requirement: Least squares assumes that the variance of the error terms is constant across all levels of the independent variables. If the data exhibits heteroscedasticity (variance of the errors is not constant), the method may not perform well.
• Independence of Errors: The method assumes that the errors of the prediction are uncorrelated with each other. If there is autocorrelation (errors from one prediction are correlated with errors from another), the estimations may be biased.
• Normal Distribution of Errors: For statistical inference using the least squares estimates to be valid, the errors are assumed to be normally distributed. This assumption may not hold true for all datasets, affecting the reliability of hypothesis tests and confidence intervals.

Solved Example

Question 1: Given a set of data points (xi​,yi​) for i=1,2,…,n, find the equation of the line y=mx+b that best fits these points using the least squares method.

Answer 1: To find the best fitting line y=mx+b, we use the least squares method formulas to calculate the slope m and y-intercept b:

Calculate the mean of the x-values (xˉ) and the mean of the y-values (yˉ​).

The slope m is given by:

m=[∑ⁿᵢ₌₁​(xᵢ−xˉ)(yᵢ−yˉ​)] / [∑ⁿᵢ₌₁(xᵢ−xˉ)²]

The y-intercept b is calculated using: b=yˉ​−mxˉ

Thus, the equation of the line is y=mx+b.

Question 2: Assuming the data points (1,2),(2,3), and (3,5) are to be fitted with a straight line using the least squares method, calculate the slope and y-intercept of this line.

Answer 2:

Calculate the mean of the x-values (xˉ=2) and the mean of the y-values (yˉ​=3.33).

Using the formula for the slope:

m=[(1−2)(2−3.33)+(2−2)(3−3.33)+(3−2)(5−3.33)] / [(1−2)²+(2−2)²+(3−2)²]

m=1.5

Calculate the y-intercept:

b=3.33−(1.5×2)=0.33

Therefore, the equation of the line is y=1.5x+0.33y=1.5x+0.33.

Question 3: Explain why the least squares method is preferred for fitting a line to a set of data points in comparison to other methods.

Answer 3: The least squares method is preferred because it minimizes the sum of the squares of the vertical distances (residuals) between the observed values and the values predicted by the model. This approach is statistically justified, as it produces the best possible estimates of the slope and intercept for linear regression, assuming the residuals are normally distributed and homoscedastic. It is efficient, minimizing prediction errors, and widely applicable, making it a standard method in linear regression analysis.

Short Questions

1. What is the formula for the slope (m) in the least squares method for a linear fit?

• Formula: m=∑(xi​−x)²∑(xi​−x)(yi​−y​)​
• Answer: This formula calculates the slope of the best-fit line by dividing the covariance of x and y variables by the variance of x, using the least squares method.

2. How do you calculate the y-intercept (b) in the least squares regression line equation?

• Formula: b=y​ˉ−mxˉ
• Answer: The y-intercept of the least squares regression line is found by subtracting the product of the slope (m) and the mean of x values (‾x) from the mean of y values (‾y​).

3. What is the least squares criterion for a best-fit line?

• Formula: Minimize ∑(yᵢ​−(mxᵢ​+b))²
• Answer: The least squares criterion aims to minimize the sum of the squares of the vertical distances (residuals) between the observed values (yᵢ​​) and the values predicted by the model (mxᵢ​+b).

4. How is the coefficient of determination (R²) calculated in the context of the least squares method?

• Formula: R²=1−[∑(yᵢ​​−y^​ᵢ​)² / ∑(yᵢ​​−yˉ​)²]
• Answer: R²measures the proportion of the variance in the dependent variable that is predictable from the independent variable(s) in the least squares regression, calculated by one minus the ratio of the sum of squared residuals to the total sum of squares.

5. Write the equation for a least squares regression line.

• Formula: y=mx+b
• Answer: This is the general form of the least squares regression line, where y is the predicted value, m is the slope, x is the independent variable, and b is the y-intercept

FAQs

What is Least Squares for Dummies?

Least squares is a statistical method used to determine the best-fit line through a set of points by minimizing the sum of the squares of the vertical distances (residuals) between the points and the line. This technique is widely used in data fitting.

What is the Rules of Least Squares?

The primary rule of least squares is to find the parameters of the line (slope and intercept) that minimize the sum of the squared differences between the observed values and the values predicted by the line. This ensures the best possible accuracy of the model.

How Do You Use the Least Square Method?

To use the least square method, first calculate the slope and intercept of the best-fit line using the formulas derived from the data points. Then, apply these parameters to predict values or analyze the relationship between variables, ensuring the residuals are minimized.

What is Least Squares for Dummies? (Repeated)

Least squares is an approach to fitting a mathematical model to data by minimizing the differences between observed values and the values predicted by the model. It’s ideal for finding the line of best fit in linear regression.

What is the Rules of Least Squares? (Repeated)

The fundamental rule in least squares involves adjusting the model parameters to minimize the sum of squared residuals, ensuring that the fitted line represents the best approximation of the observed data.

How Do You Use the Least Square Method? (Repeated)

Employing the least square method involves identifying the linear equation that best models the data by minimizing the square of the difference between observed and predicted values, typically used for predicting outcomes or understanding relationships.