Perimeter of a Rectangle – 10+ Examples, Definition, Formula, How to find, Usage

The perimeter of a shape is the total distance around its edge. To calculate the perimeter of a rectangle, we add up the lengths of all its sides. However, because each pair of opposite sides in a rectangle is equal, we just need to know the rectangle’s length and width. The formula for the perimeter of a rectangle is to multiply the sum of the length and width by two. Perimeter is measured in units like meters, centimeters, inches, or feet.

What is the Perimeter of a Rectangle?

Perimeter of a Rectangle Formula

To calculate the perimeter of a rectangle, you can use a simple mathematical formula. The formula is based on the properties of a rectangle, where opposite sides are equal in length. Here is how you determine the perimeter:

This formula means that you first add the length and the width of the rectangle. After getting the total of these two dimensions, you multiply the result by two. This calculation gives you the total distance around the rectangle.

How to Find the Perimeter of a Rectangle?

1. Identify the Dimensions: Determine the length and the width of the rectangle. These are usually given in problems or can be measured if you’re dealing with a physical object.
2. Use the Perimeter Formula: Apply the formula for the perimeter of a rectangle, which is: Perimeter = 2 × (Length + Width)This formula works because a rectangle has two sets of opposite sides that are each equal in length. By adding the length and the width together and then doubling that sum, you capture the total distance around the rectangle.
3. Calculate: Plug the measurements of the length and width into the formula. Add these two figures together, then multiply the sum by two to get the perimeter.
4. Express in Units: Ensure that the perimeter is expressed in the same units as the measurements for length and width (such as meters, feet, or inches).

Example:

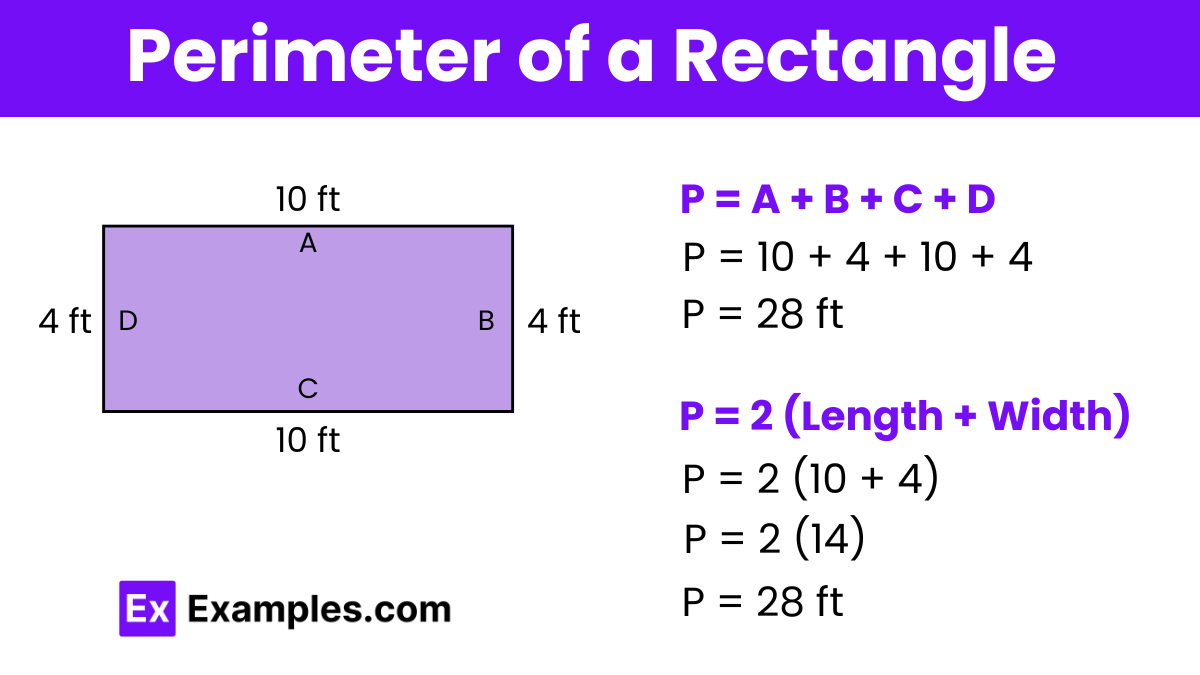
Suppose a rectangle has a length of 10 feet and a width of 4 feet. Here’s how you would calculate the perimeter:

• Perimeter = 2 × (10 feet + 4 feet) = 2 × 14 feet = 28 feet

So, the perimeter of this rectangle is 28 feet. This calculation is useful for various practical applications, such as figuring out the amount of material needed for a border or fence around the rectangle.

Examples using Perimeter of Rectangle Formula

Example 1: Basic Calculation

Problem: A rectangle has a length of 6 meters and a width of 2 meters. What is the perimeter?

Solution:

• Formula: Perimeter = 2 × (Length + Width)
• Calculation: Perimeter = 2 × (6 m + 2 m) = 2 × 8 m = 16 meters
• Answer: The perimeter of the rectangle is 16 meters.

Example 2: Finding the Required Material

Problem: You need to install a fence around a rectangular garden that measures 15 feet in length and 10 feet in width. How much fencing material will you need?

Solution:

• Formula: Perimeter = 2 × (Length + Width)
• Calculation: Perimeter = 2 × (15 ft + 10 ft) = 2 × 25 ft = 50 feet
• Answer: You will need 50 feet of fencing material.

Example 3: Framing a Picture

Problem: A rectangular picture measures 8 inches by 5 inches. How much framing material is needed to frame the picture?

Solution:

• Formula: Perimeter = 2 × (Length + Width)
• Calculation: Perimeter = 2 × (8 in + 5 in) = 2 × 13 in = 26 inches
• Answer: You need 26 inches of framing material.

Example 4: Sizing a Classroom Border

Problem: A teacher wants to put a decorative border around a rectangular bulletin board that is 12 feet long and 7 feet wide. Calculate the amount of border required.

Solution:

• Formula: Perimeter = 2 × (Length + Width)
• Calculation: Perimeter = 2 × (12 ft + 7 ft) = 2 × 19 ft = 38 feet
• Answer: 38 feet of decorative border is required.

Usage of Perimeter of a Rectangle

1. Construction and Building Projects

In construction, knowing the perimeter of rectangular areas like rooms, gardens, or plots of land helps in estimating the amount of materials needed. For example, builders calculate the perimeter to determine the length of fencing required, or the amount of baseboard needed to cover the edges of a room.

2. Crafts and Framing

In crafting, especially when creating frames, the perimeter measurement helps in cutting the right amount of framing material to ensure each side is covered perfectly. Whether it’s a picture frame or a crafted box, the perimeter tells you exactly how much material you’ll need around the edges.

3. Fabrication and Manufacturing

In the manufacturing sector, knowing the perimeter of items can be crucial for fabricating everything from the material needed for the edges of a rectangular metal plate to the trim around textile pieces. This helps in minimizing waste and optimizing the use of materials.

4. Interior Design and Decoration

Interior designers use the perimeter of floors and walls to calculate the quantities of materials needed for projects. This could include the amount of paint required to cover the borders of a room, or the length of decorative trim or crown molding.

5. Agriculture and Landscaping

Farmers and landscapers often calculate the perimeter of rectangular fields and plots to figure out the quantities of materials needed for tasks like installing irrigation systems, fencing, and pathways. Knowing the perimeter helps in budgeting and resource allocation.

6. Educational Purposes

In educational settings, teachers use the concept of perimeter to help students understand geometry, measurement, and arithmetic operations. It serves as a practical example to illustrate the application of mathematical concepts in real life.

7. Sports and Recreational Areas

Calculating the perimeter of rectangular sports fields, such as soccer fields or tennis courts, helps in planning the layout and ensuring the correct dimensions for boundary lines or nets.

Relationship Between Area and Perimeter of a Rectangle

The area and perimeter of a rectangle are related through the rectangle’s length and width, but they do not directly influence each other. Changing one dimension affects both the area and the perimeter, but the extent of their change depends on how the dimensions are altered. Here are a few key insights:

1. Proportional Changes: If you increase or decrease both the length and the width of a rectangle by the same proportion, the area changes more dramatically than the perimeter. The area is a product of the two dimensions (making it grow or shrink exponentially), while the perimeter is a sum of the two dimensions.
2. Independent Variations: Increasing one dimension (length or width) while keeping the other constant will increase both the area and the perimeter, but at different rates. The area will increase linearly with the increase in one dimension, while the perimeter’s increase is also linear but less dramatic.
3. Geometric Interpretation: A smaller perimeter does not necessarily mean a smaller area, and vice versa. For instance, two rectangles can have the same perimeter but very different areas, depending on their length-to-width ratios.

Practical Example

Consider two rectangles:

• Rectangle A: Length = 4 m, Width = 3 m
• Rectangle B: Length = 6 m, Width = 1 m

Both rectangles have the same perimeter:

• Perimeter of A = 2 × (4 m + 3 m) = 14 m
• Perimeter of B = 2 × (6 m + 1 m) = 14 m

However, their areas are different:

• Area of A = 4 m × 3 m = 12 m²
• Area of B = 6 m × 1 m = 6 m²

FAQs

How do you find the perimeter area of a rectangle?

To find the perimeter of a rectangle, add the lengths of all four sides: formula is 2×(length+width).

What is an example of a perimeter?

An example of a perimeter is measuring the total length around a garden to determine how much fencing is needed.

How do you explain perimeter to a child?

Explain perimeter to a child as the measurement around the edge of a shape, like tracing the outline with a string.

How do you find the perimeter for kids?

Teach kids to find the perimeter by adding up the lengths of all the sides of the shape they’re measuring.

What does a perimeter look like in math?

In math, a perimeter appears as a line measurement around a two-dimensional shape, represented by numbers indicating its total length.