Area

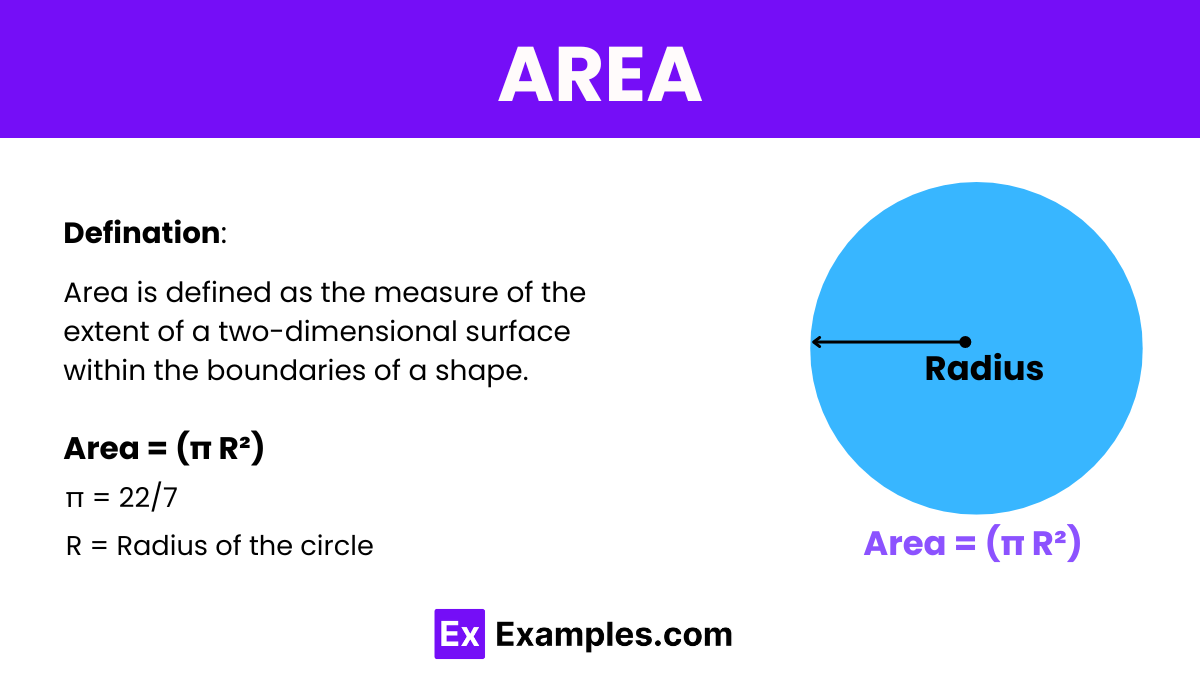
Area is a mathematical concept that describes the size of a two-dimensional surface. It is quantified in square units, reflecting the size of the surface. The calculation methods and formulas for area vary depending on the shape, such as using length times width for rectangles or base times height divided by two for triangles. Area is a fundamental concept used in geometry, science, engineering, and daily life to determine how much space a shape covers.

What Is a Area?

Area is defined as the measure of the extent of a two-dimensional surface within the boundaries of a shape

It is calculated by multiplying the length and width of a shape or by other formulas specific to different shapes, such as circles or triangles. The result is expressed in square units, such as square meters or square feet, indicating the total space enclosed within the boundaries of the shape. Area is a critical measure in various fields, including architecture, land development, and interior design, where understanding the extent of surfaces is essential.

Tools to Measure Area

1. Aerial Drones: Equipped with cameras and GPS, drones can capture images of large tracts of land from above. Software can then analyze these images to calculate area, useful in agriculture, surveying, and environmental monitoring.
2. 3D Scanners: These devices can scan the environment in three dimensions and are useful in calculating the surface area of irregular objects or terrains. This technology is invaluable in industries like manufacturing, where surface area measurements can affect material properties and dynamics.
3. Stereoplotters: Used in photogrammetry, stereoplotters allow for the measurement of areas from stereoscopic aerial photographs by plotting points in a 3D space, which is essential for topographic mapping.
4. Satellite Imaging: Satellite images are used to measure large areas such as forests, bodies of water, or agricultural fields. Software analyzes the images to calculate areas based on the pixels that each represents.
5. Ground Penetrating Radar (GPR): While traditionally used to detect objects underground, GPR can be adapted to measure the area by scanning surface boundaries, especially in uneven terrain.
6. Hydrographic Survey Equipment: Used to measure and calculate areas underwater, such as the bed of a lake, river, or sea, often using sonar technology.

Formulas for Calculating Area

Shape	Formula
Square	Area = side²
Rectangle	Area = length × width
Triangle	Area = 1/2 × base × height
Circle	Area = π × radius²
Trapezoid	Area = 1/2 × (base1+base2) × height
Parallelogram	Area = base × height
Ellipse	Area = π × radius1 × radius2
Rhombus	Area=1/2 × diagonal1 × diagonal2

Difference Between Area and Perimeter

Aspect	Area	Perimeter
Definition	Area is the measure of the space inside a two-dimensional shape.	Perimeter is the total length of the edges or boundary of a shape.
Measurement Units	Measured in square units (e.g., square meters, square feet).	Measured in linear units (e.g., meters, feet).
Calculation	Involves multiplication or more complex mathematical formulas depending on the shape (e.g., length × width for rectangles, π × radius² for circles).	Involves addition of all the side lengths of a shape.
Purpose	Used to determine the amount of material needed to cover a shape, such as flooring or paint.	Used to find the length of material needed to enclose a shape, such as fencing around a yard.
Dependency	Area calculation depends on the shape’s dimensions but not on its position or orientation.	Perimeter measurement is independent of the shape’s position but depends solely on the length of its sides.
Shape Impact	Two shapes with the same perimeter can have different areas.	Two shapes with the same area can have different perimeters.
Practical Example	Calculating the amount of carpet needed to cover a room.	Determining the amount of molding required to go around the edges of that room.

Units of Measurement for Area

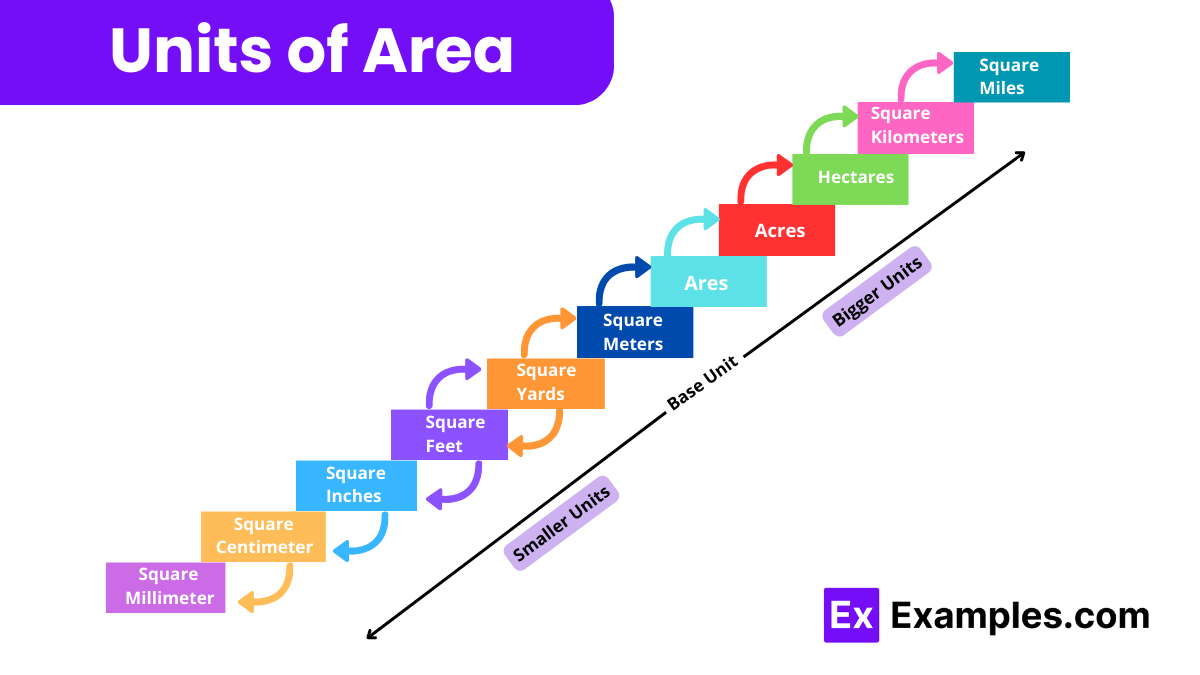
The measurement of area is expressed in units that are derived from the square of a length unit. Here’s a look at the common units used to measure area:

• Square Meters (m²): The most common unit of area in the metric system, used widely around the world to measure smaller plots of land, rooms, or large furniture surfaces.
• Hectares (ha): Primarily used in agriculture and forestry, one hectare is equivalent to 10,000 square meters (100m x 100m). It’s useful for measuring larger tracts of land.
• Square Kilometers (km²): Used for measuring larger areas, such as geographical regions or cities. One square kilometer equals one million square meters.
• Square Centimeters (cm²): Used to measure smaller areas in more detailed contexts, such as textiles or drawings.
• Square Millimeters (mm²): Used in smaller, precise measurements such as in some scientific research or engineering contexts.
• Acres: Predominantly used in the United States, the United Kingdom, and a few other countries, an acre is about 4,046.86 square meters or about 0.4047 hectares. It’s commonly used for measuring land properties.
• Square Feet (ft²): Often used in the United States and the UK for real estate purposes, particularly for describing the area of smaller residential or commercial properties.
• Square Yards (yd²): Less commonly used than square feet, but still relevant in fabric measurement, land area, and carpeting.
• Square Inches (in²): Used for measuring small areas, such as paper, tablet screens, and photographic prints.
• Square Miles (mi²): Used for large land areas, such as counties or states in the United States.
• Ares (a): One are is 100 square meters. It’s less common but sometimes used in land measurement in some European countries.

Methods for Calculating Area

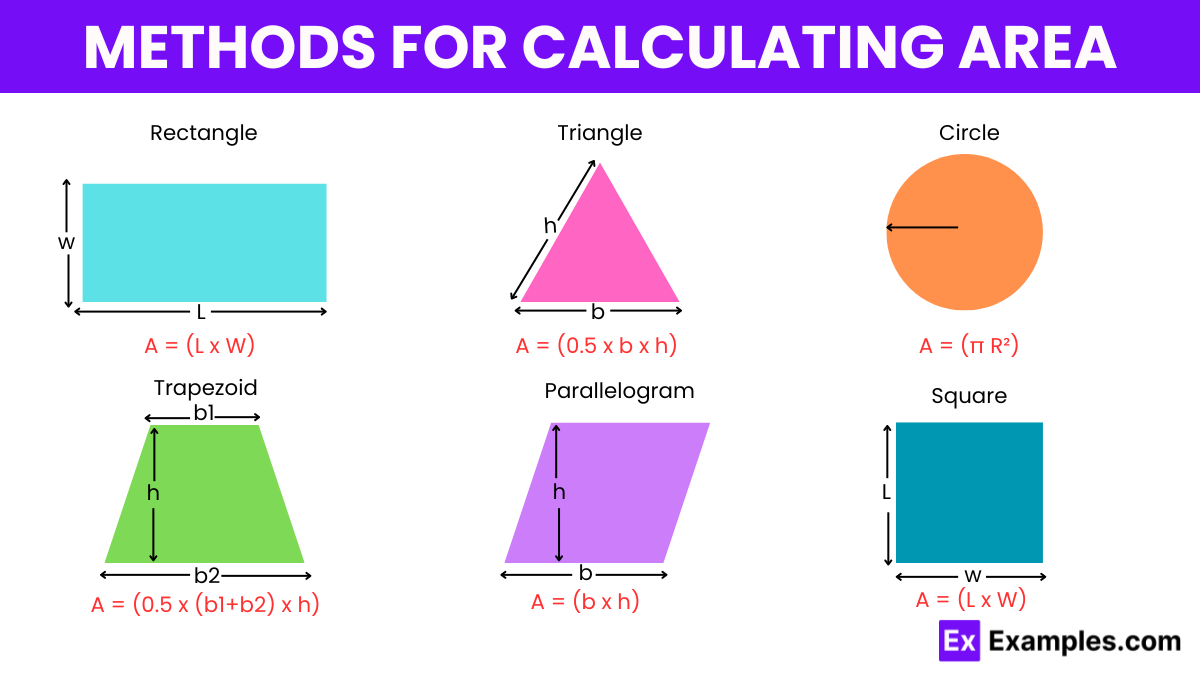
Calculating the area of various shapes requires different methods depending on the geometry of the shape. Here’s an overview of how to calculate the area for some common shapes:

Rectangle/Square:

• Formula: Area = Length × Width.
• For squares, since all sides are equal, Area = Side × Side.

Triangle:

• Formula: Area = 0.5 × Base × Height.
• This formula applies to all triangles, regardless of type (right, equilateral, isosceles, or scalene).

Circle:

• Formula: Area = π × Radius².
• π (Pi) is approximately 3.14159.

Trapezoid:

• Formula: Area = 0.5 × (Base₁ + Base₂) × Height.
• This uses the heights and the lengths of the two parallel sides.

Parallelogram:

• Formula: Area = Base × Height.
• The height is the perpendicular distance between the parallel sides.

Irregular Shapes:

• Method: Divide the shape into a combination of simpler shapes whose areas can be calculated, then sum these areas. Alternatively, use geometric or numerical methods like the shoelace formula or Monte Carlo simulations.

Sector of a Circle:

• Formula: Area = 0.5 × Radius² × Angle (in radians).
• The angle must be in radians for this formula to be correct.

Annulus (Ring):

• Formula: Area = π × (Outer Radius² – Inner Radius²).
• This calculates the area of the space between two concentric circles.

Surface Area of 3D Objects:

• For three-dimensional objects like spheres, cylinders, and cubes, the surface area is the total area covering the object’s surface.
• Examples:
• Sphere: Area = 4π × Radius².
• Cylinder: Area = 2π × Radius × (Height + Radius)

Challenges in Area Calculation

Calculating the area can present various challenges depending on the complexity and accessibility of the shape or region in question. Here are some common challenges:

1. Irregular Shapes: Measuring areas of irregularly shaped fields or plots can be complex, requiring more sophisticated methods like triangulation or integration.
2. Scale and Precision: For very large or small areas, maintaining accuracy in measurements and calculations can be difficult, impacting the precision of the area calculated.
3. Topography: In real-world scenarios like land measurement, uneven terrain or obstacles can make it hard to measure and calculate the exact area.
4. Measurement Tools: Limited access to accurate tools or reliance on outdated methods can result in errors in the calculation of areas.
5. Mathematical Complexity: Some shapes require advanced mathematics for area calculation, such as integration for curves and shapes with non-linear boundaries, which might not be straightforward for all users.

Uses of Area

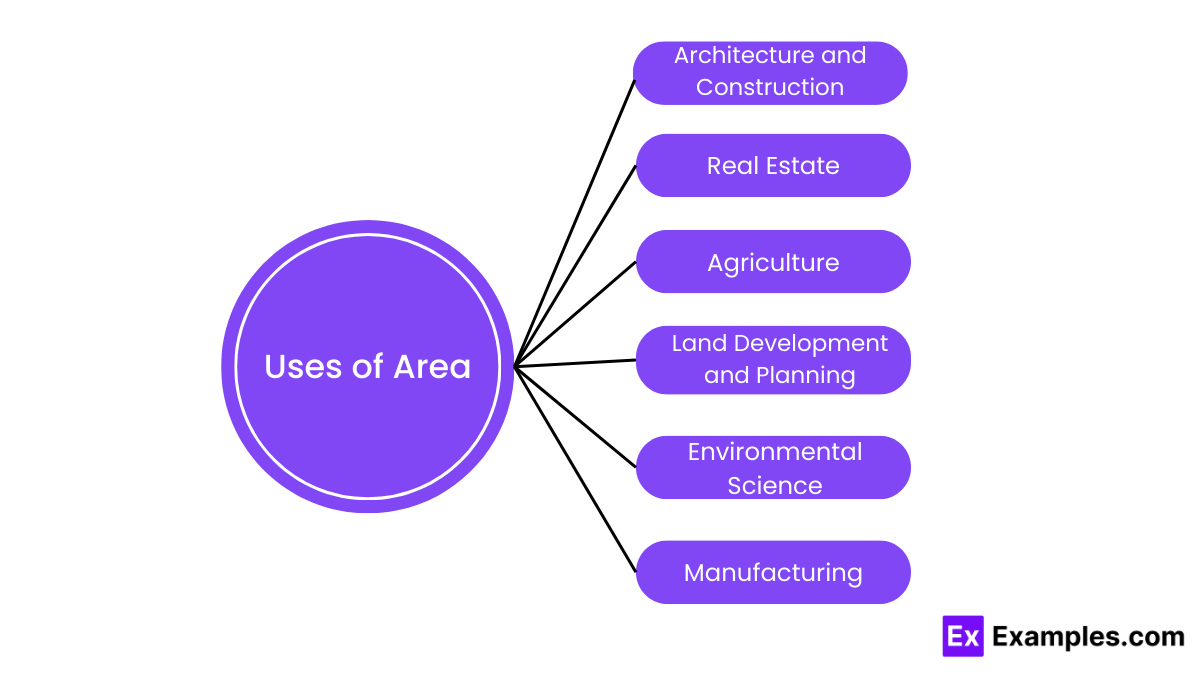
The concept of area is used in numerous fields and applications, reflecting its fundamental importance across various disciplines. Here are some key uses of area:

1. Architecture and Construction: Architects and builders use area calculations to design buildings and structures, determining the amount of materials needed for construction, such as flooring, roofing, and paint.
2. Real Estate: Area measurements are crucial in the real estate industry to determine the size of properties, which influences their market value and utility.
3. Agriculture: Farmers need to know the area of their land to manage irrigation systems, calculate seeding requirements, and estimate potential yields.
4. Land Development and Planning: Urban planners use area calculations to design community layouts, including placement of parks, residential areas, and commercial zones.
5. Environmental Science: Area calculations help in environmental conservation, such as estimating the size of protected areas, assessing deforestation impacts, and managing habitats.
6. Manufacturing: In manufacturing, knowing the area of materials is essential for cutting raw materials into pieces with minimal waste.

FAQ’S

What is area of shape?

The area of a shape is the measure of the surface it covers, expressed in square units like square meters or square feet. It quantifies the two-dimensional space enclosed.

How is area measured?

Area is measured by calculating the space within the boundaries of a shape using specific formulas or tools, depending on the shape’s geometry and size.

What shape has the most area?

Among basic shapes, the circle has the most area relative to its perimeter, making it the most efficient shape for enclosing space.