Rectangle – Definition, Shape, Properties, Formulas, Types

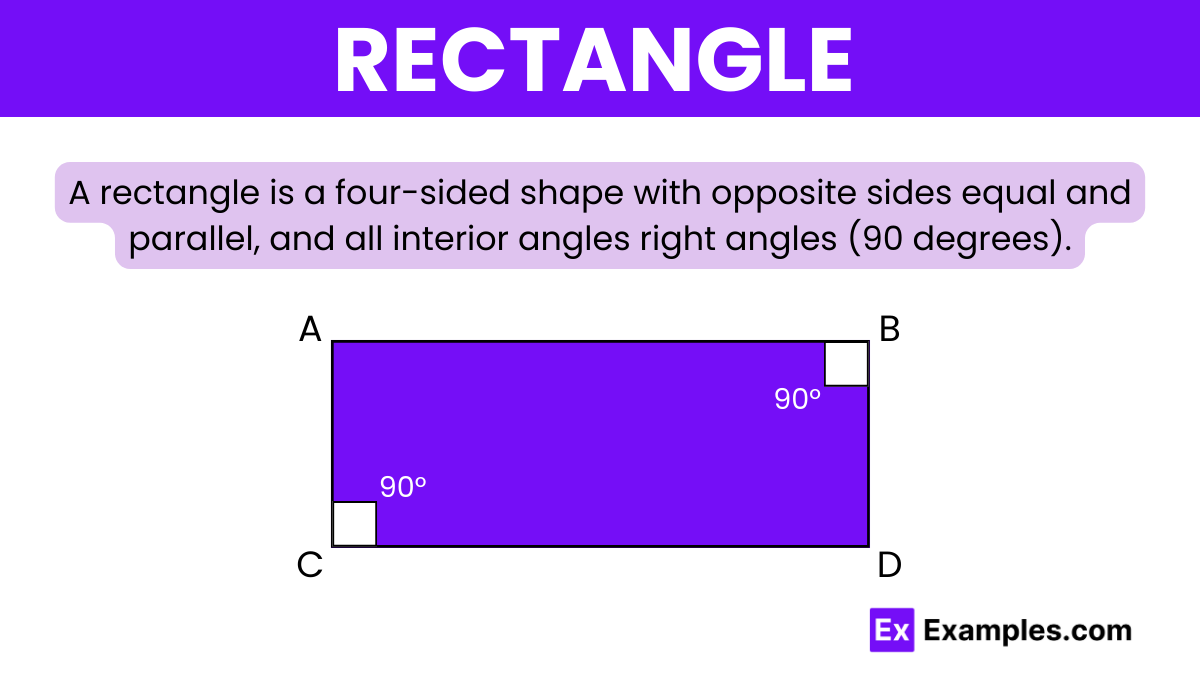
A rectangle is a four-sided shape where every angle is the same and opposite sides are the same length and run parallel to each other. We see objects shaped like rectangles all around us. To describe a rectangle, we use two measurements: its length and its width. The length is the longer side, while the width is the shorter side.

What is Rectangle?

Shape of Rectangle

A rectangle is a simple shape with four sides and four corners, where every corner is a sharp 90-degree angle. This means the sides facing each other are exactly the same length and run perfectly parallel. The longer sides are known as the length and the shorter sides as the width.

Rectangles are everywhere around us! Think about doors, books, smartphones, and TVs—these are all everyday objects shaped like rectangles. This common shape is not only easy to recognize but also fundamental in both daily life and various fields such as architecture, art, and mathematics.

Length and Width of Rectangle

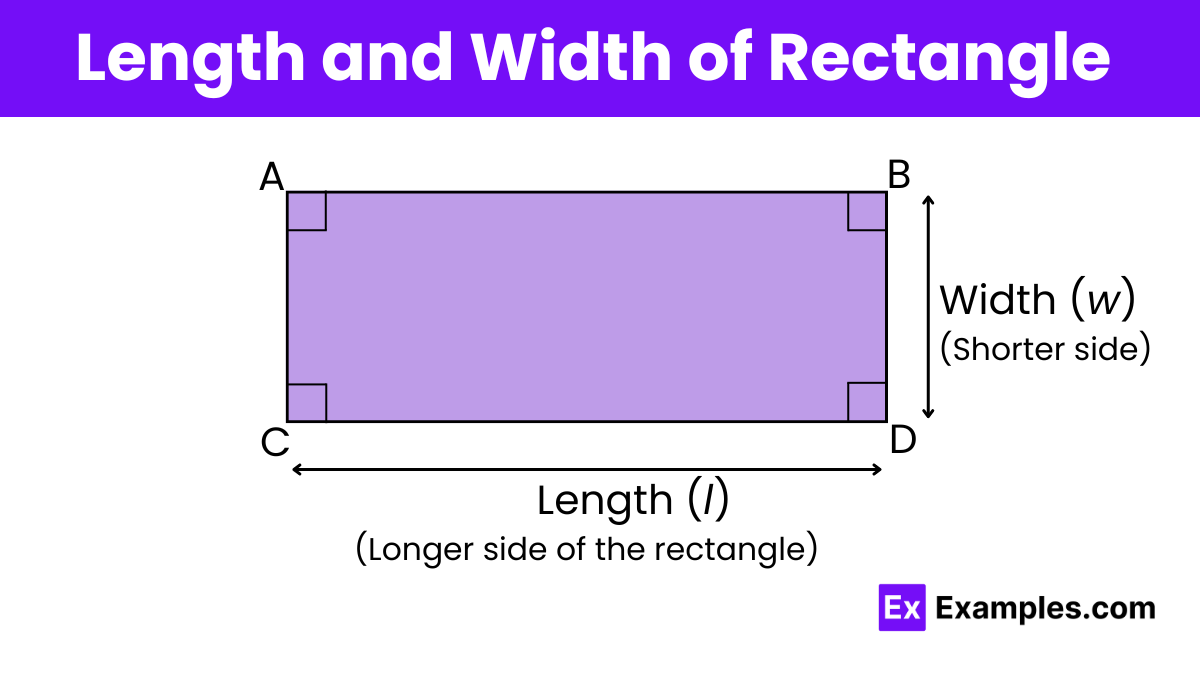
In a rectangle, the length and width (also known as breadth) are the two key measurements that define its shape. The length refers to the longer side of the rectangle, while the width refers to the shorter side. These dimensions give us a clear understanding of the size and proportion of the rectangle.

When measuring a rectangle, the length typically runs horizontally, and the width runs vertically when drawn on paper or displayed on a screen. These dimensions are crucial for calculations involving area and perimeter, helping us understand how much space the rectangle covers and how much material might be needed to outline it. Rectangles are practical in design and construction because their predictable measurements make planning and building easier.

Properties of a Rectangle

Rectangle Formulas

1. Area: The area of a rectangle is calculated by multiplying the length by the width.
   • Formula: Area = length×width
2. Perimeter: The perimeter of a rectangle is the total distance around the boundary of the shape. It is calculated by adding together the lengths of all four sides.
   • Formula: Perimeter = 2×(length+width)
3. Diagonal Length: The length of each diagonal in a rectangle can be calculated using the Pythagorean theorem, as the rectangle’s diagonals create right triangles with the length and width.
   • Formula: Diagonal = √length²+width²

Diagonal of a Rectangle

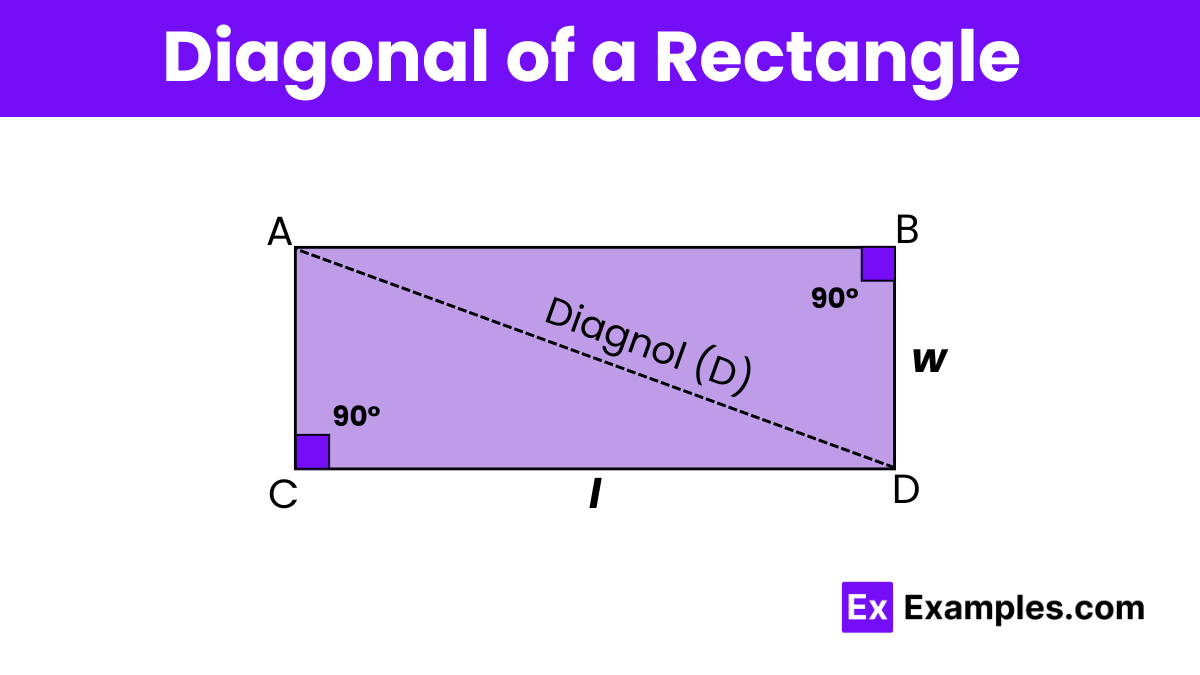
The diagonal of a rectangle is a line that connects two opposite corners, or vertices, that aren’t next to each other. In a rectangle, you can see this with diagonals AC and BD, which are the same length. Each diagonal splits the rectangle into two right-angled triangles, with the diagonal acting as the longest side, called the hypotenuse, and the rectangle’s length and width as the triangle’s other two sides.

Diagonal of Rectangle Formula

To find the length of a rectangle’s diagonal, we use the Pythagoras theorem. Imagine you have a rectangle with a length ‘l’ and a width ‘w’. Let ‘d’ be the length of the diagonal. According to the Pythagoras theorem, in triangle ABD, the equation would be d² = l²+w². By taking the square root of both sides, you get d = √l²+w²​. This gives us the formula to calculate the diagonal of a rectangle:

Types of Rectangle

1. Square: A square is a highly symmetrical type of rectangle where all four sides are equal in length. This uniformity means each of the angles is also a right angle (90 degrees), like in other rectangles. Squares stand out because of their equal sides and because they possess both the properties of a rectangle and a rhombus (a shape with all sides equal but not necessarily having right angles). Due to their symmetry, squares are often used in design and architecture, providing a sense of balance and uniformity.

2. Golden Rectangle: The golden rectangle is a rectangle whose side lengths are in the golden ratio, approximately 1:1.618. This type of rectangle is famous for its aesthetic appeal and has been used in various art forms and architectural designs throughout history. The golden rectangle is believed to be visually pleasing and naturally occurring in nature, making it a favorite choice for artists and architects. The unique property of a golden rectangle is that when a square is removed from it, the leftover rectangle is also a golden rectangle, allowing this division to continue indefinitely.

3. Credit Card Rectangle: This rectangle has a standardized aspect ratio of approximately 1:1.586, mirroring the dimensions of a credit card. The size and shape are designed to fit perfectly into wallets and card slots, making it a practical application of rectangular design in everyday life. The credit card rectangle is also a great example of how rectangles are used in functional design, ensuring compatibility with various devices and holders.

4. Standard Rectangle: A standard rectangle, simply referred to as a rectangle, is any shape with four sides where the opposite sides are equal in length and all interior angles are right angles. This category covers a wide range of rectangles without a fixed ratio between the length and width, making it the most general and commonly recognized type. Standard rectangles are everywhere, from paper sheets to smartphone screens, illustrating how versatile and fundamental this shape is in both practical and theoretical applications.

5. Fibonacci Rectangle: Constructed using the Fibonacci sequence, this rectangle is made by piecing together squares whose sides are Fibonacci numbers, and the resulting shape approaches the golden rectangle as more squares are added. This type also exhibits aesthetically pleasing properties and is used in theoretical mathematics and design.

Components of Rectangle

A rectangle is a fundamental shape in geometry, consisting of several key components that define its structure and properties. Here’s an overview of the main components of a rectangle:

1. Sides:
   • A rectangle has four sides. The opposite sides of a rectangle are equal in length and parallel to each other. There are two longer sides (length) and two shorter sides (width).
2. Vertices:
   • The rectangle has four vertices, or corners, where the sides meet. Each vertex forms a right angle, meaning each angle is 90 degrees.
3. Angles:
   • There are four interior angles in a rectangle, each measuring exactly 90 degrees. The consistency of right angles is a defining characteristic of rectangles.
4. Diagonals:
   • A rectangle contains two diagonals that crisscross the shape, connecting opposite vertices. The diagonals are equal in length and bisect each other, which means they cut each other exactly in half at the center of the rectangle.
5. Perimeter:
   • The perimeter is the total distance around the outside of the rectangle. It is calculated by adding together the lengths of all four sides. The formula for the perimeter of a rectangle is 2×(length+width).
6. Area:
   • The area represents the total space contained within the rectangle. It is calculated by multiplying the length by the width. The formula for the area of a rectangle is length×width.

When will children learn about rectangles?

1. Preschool (Ages 3-4):
   • At this stage, children are introduced to simple shapes through play and informal learning. They start recognizing and naming shapes like circles, squares, triangles, and rectangles. Activities might include sorting shapes or identifying shapes in everyday objects.
2. Kindergarten (Ages 5-6):
   • In kindergarten, children learn more formally about different shapes, including rectangles. They explore the properties of shapes, such as the number of sides and angles. Teachers might use shape blocks, drawing exercises, and interactive games to reinforce these concepts.
3. Elementary School (Ages 6-10):
   • As they progress through elementary school, students delve deeper into the properties and mathematics of shapes. They learn about the area and perimeter of rectangles, understand the concept of right angles, and start using shapes in mathematical problems and geometry lessons. Activities could include using rulers to draw rectangles and calculate their area and perimeter.
4. Middle School (Ages 11-13):
   • By middle school, students expand their knowledge of geometry to include more complex concepts involving rectangles and other polygons. They might learn about the Pythagorean theorem, using it to calculate the diagonals of rectangles, and explore concepts like scale and proportion using rectangular shapes.

Which shape is a rectangle?

A rectangle is a four-sided shape with opposite sides equal and all angles at 90 degrees.

Why does a rectangle have 4 sides?

A rectangle has four sides to form a closed, two-dimensional shape with opposite sides equal and parallel, fulfilling the properties of a quadrilateral.

Is a rectangle never a rhombus?

Typically, a rectangle is not a rhombus because its sides are of unequal lengths, unlike a rhombus where all sides are equal.

Is an oblong a rectangle?

Yes, an oblong is a type of rectangle with length significantly greater than width, often referred to in everyday language.

Is A rectangle a parallelogram?

Yes, a rectangle is a type of parallelogram with the added property that all its angles are right angles.

Are rectangles always trapezoids?

Technically, rectangles can be considered trapezoids with one pair of parallel sides, though this classification is not commonly used.

Can a square be a rectangle?

Yes, a square is a special type of rectangle where all four sides are equal in length and all angles are 90 degrees.