Factors of 20

The factors of a number is fundamental in mathematics. The number 20 is a composite number, meaning it has several factors. Factors are numbers that divide the original number exactly without leaving a remainder. For 20, these include 1, 2, 4, 5, 10, and 20. Knowing the factors of 20 is useful in various mathematical applications, such as simplifying fractions, finding common denominators, and solving algebraic equations. Exploring the factors of 20 can also provide insight into its divisibility and the relationships between numbers, enhancing your overall grasp of number theory and arithmetic.

What are the Factors of 20?

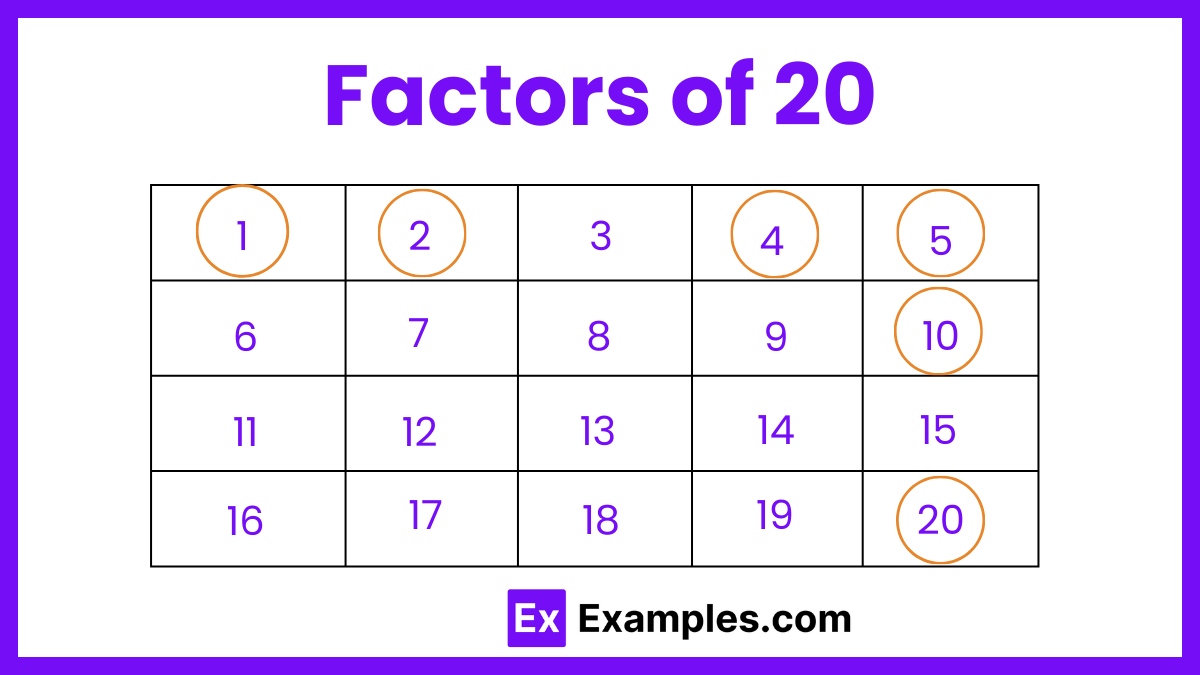
The factors of 20 are 1, 2, 4, 5, 10, and 20. These numbers divide 20 exactly without leaving a remainder. Understanding the factors helps in simplifying fractions and solving mathematical problems. As a composite number, 20 has multiple factors, making it useful for various applications in arithmetic and number theory.

Factors Pairs of 20

The factor pairs of 20 are as follows:

• (1, 20): When 1 is multiplied by 20, the product is 20.
• (2, 10): When 2 is multiplied by 10, the product is 20.
• (4, 5): When 4 is multiplied by 5, the product is 20.
• (-1, -20): When -1 is multiplied by -20, the product is 20.
• (-2, -10): When -2 is multiplied by -10, the product is 20.
• (-4, -5): When -4 is multiplied by -5, the product is 20.

These pairs include both positive and negative factors, all resulting in the product of 20.

How to Calculate Prime Factors of 20?

Calculating the prime factors of a number involves breaking it down into its basic prime number components. Prime numbers are those that have no divisors other than 1 and themselves. For composite numbers like 20, this process helps in understanding its structure and simplifying mathematical operations. Here’s how you can calculate the prime factors of 20.

Step 1: Start with the Smallest Prime Number

• Begin with the smallest prime number, which is 2. Check if 20 is divisible by 2.

Step 2: Divide by the Smallest Prime

Since 20 is even, it is divisible by 2. Divide 20 by 2 to get 10.
20 ÷ 2 = 10

Step 3: Continue with the Quotient

Now take the quotient (10) and check if it is divisible by 2. Since 10 is also even, divide by 2 again.
10 ÷ 2 = 5

Step 4: Move to the Next Prime Number

Now, take the new quotient (5). Check if it is divisible by 2. Since 5 is not even, it is not divisible by 2.
Move to the next smallest prime number, which is 3. 5 is not divisible by 3 either.

Step 5: Confirm the Remaining Number is Prime

The next prime number is 5. Since 5 is a prime number and is divisible by itself, the process ends here.
5 ÷ 5 = 1

Step 6: List All Prime Factors

The prime factors of 20 are the prime numbers you used in the division process: 2, 2, and 5.
Therefore, the prime factorization of 20 is 2 × 2 × 5 or 2²×5.

Factors of 20: Examples

Example 1: Identifying Factors of 20

• Problem: Determine the factors of 20.
• Solution: The factors of 20 are the numbers that divide 20 exactly without leaving a remainder. These numbers are 1, 2, 4, 5, 10, and 20.
• Answer: 1, 2, 4, 5, 10, 20

Example 2: Sum of Factors of 20

• Problem: Find the sum of all factors of 20.
• Solution: The factors of 20 are 1, 2, 4, 5, 10, and 20. Add these factors together: 1 + 2 + 4 + 5 + 10 + 20 = 42.
• Answer: 42

Example 3: Product of Factor Pairs of 20

• Problem: Calculate the product of factor pairs (2 and 10) of 20.
• Solution: Multiply the pair of factors: 2 × 10 = 20.
• Answer: 20

Example 4: Prime Factorization of 20

• Problem: Perform the prime factorization of 20.
• Solution: Divide 20 by the smallest prime number (2) to get 10, then divide 10 by 2 to get 5. Since 5 is a prime number, the prime factorization of 20 is 2 × 2 × 5, or 2²×5.
• Answer: 2²×5

Example 5: Checking Divisibility by Factors of 20

• Problem: Verify if 20 is divisible by 4.
• Solution: Divide 20 by 4. Since 20 ÷ 4 = 5, which is a whole number, 20 is divisible by 4.
• Answer: Yes, 20 is divisible by 4.

Factors of 20 : Tips

The factors of a number is crucial for various mathematical applications. The number 20 is a composite number with multiple factors. These factors can be useful in simplifying fractions, solving equations, and understanding number theory. Here are some tips to help you work with the factors of 20 effectively.

1. Identify all factors: Remember that the factors of 20 are 1, 2, 4, 5, 10, and 20. These numbers divide 20 exactly without leaving a remainder.
2. Understand factor pairs: Factor pairs of 20 are (1, 20), (2, 10), and (4, 5). These pairs multiply together to give 20.
3. Use prime factorization: The prime factors of 20 are 2 and 5. The prime factorization is 22×522×5.
4. Simplify fractions: Use the factors of 20 to simplify fractions where 20 is the numerator or denominator. For example, 20/40 simplifies to 1/2.
5. Solve equations: Recognize that factors can help solve equations involving 20, such as finding the roots of quadratic equations.
6. Check divisibility: Use the factors to quickly determine if 20 is divisible by another number, such as 2, 4, 5, and 10.
7. Apply in real-world problems: Use factors in practical applications like dividing items into equal groups or understanding ratios.
8. Enhance number theory skills: Studying the factors of 20 can improve your understanding of divisibility rules, prime numbers, and composite numbers.

What is the sum of the factors of 20?

The sum of the factors of 20 is 1 + 2 + 4 + 5 + 10 + 20 = 42.

How is the prime factorization of 20 written?

The prime factorization of 20 is written as 2²×5

What is the greatest common factor (GCF) of 20 and 30?

The greatest common factor of 20 and 30 is 10, as 10 is the largest number that divides both 20 and 30 exactly.

What is the product of all the factors of 20?

The product of all the factors of 20 (1, 2, 4, 5, 10, 20) is 1 × 2 × 4 × 5 × 10 × 20 = 8,000.

Is 5 a factor of 20?

Yes, 5 is a factor of 20. When 20 is divided by 5, it results in an integer (20 ÷ 5 = 4), meaning 5 divides 20 exactly without leaving a remainder.

How can knowing the factors of 20 be useful?

Knowing the factors of 20 is useful for simplifying fractions, solving equations, finding common denominators, and understanding properties of numbers in mathematics.