Which number is both rational and real?
4
π
i
√2


Discovering the world of numbers opens doors to understanding fundamental concepts in mathematics. From the simplicity of counting to the complexity of advanced calculations, numbers are the building blocks of mathematical exploration. In this comprehensive guide, we delve into the intricacies of numbers, exploring their properties, classifications, and applications. Whether you’re a student seeking clarity or a curious mind eager to delve deeper, join us on a journey through the fascinating realm of numbers, enriched with vivid examples and practical insights.
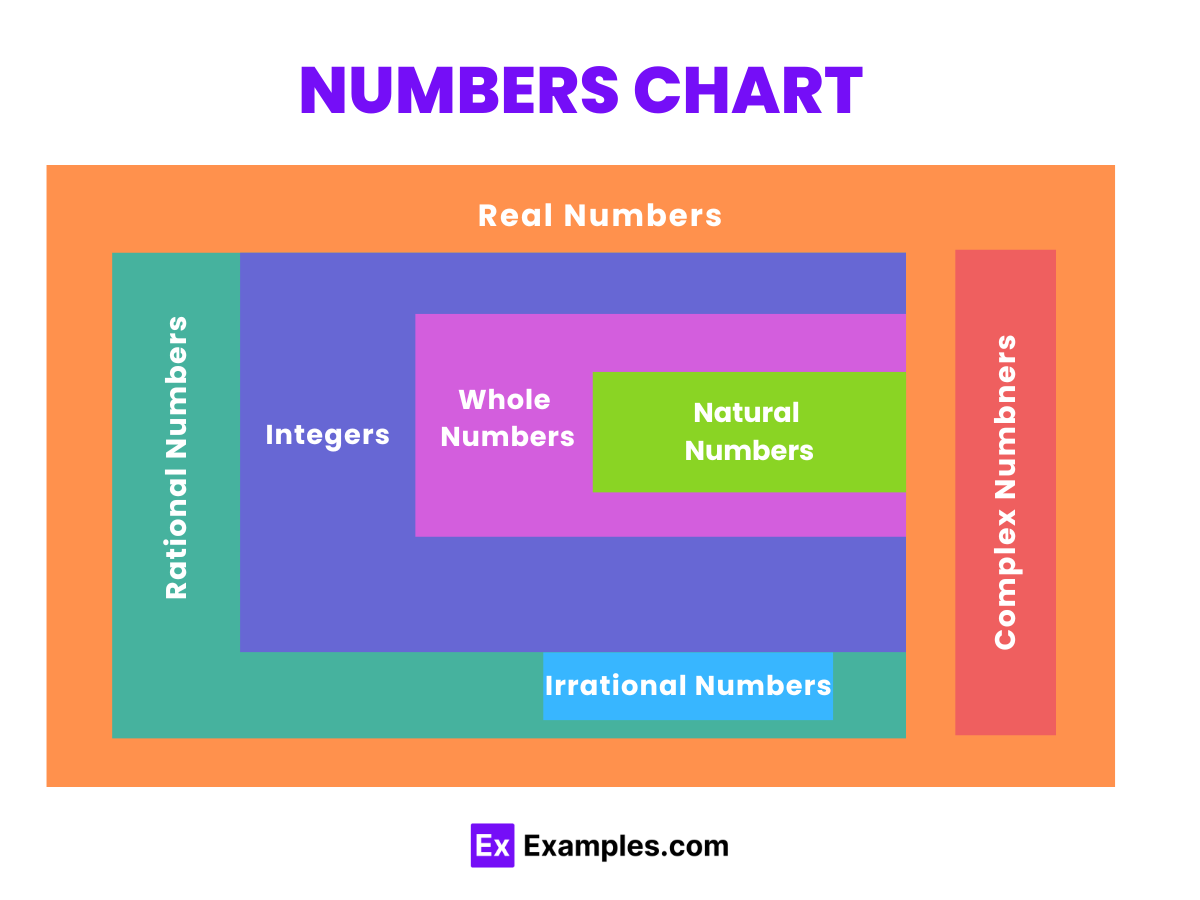
Numbers are the fundamental building blocks of mathematics, used to quantify, measure, label, and order objects in the world around us. They come in various forms, including natural numbers, integers, rational numbers, and irrational numbers, each serving distinct purposes in mathematical calculations and everyday life. From simple counting to representing complex data in science and engineering, numbers enable us to comprehend and interact with the universe. Understanding the different types of numbers and their properties is crucial for students embarking on their mathematical education journey, providing the tools needed for problem-solving and logical reasoning.
Counting numbers, also known as natural numbers, start from 1 and go on infinitely (1, 2, 3, …). They are the basic set of numbers used for counting objects and represent quantities in real life. For example, counting the number of students in a classroom or the number of apples in a basket employs counting numbers. These numbers are foundational in mathematics, teaching basic arithmetic operations like addition and subtraction.
The number zero (0) holds a unique position in the world of numbers. It acts as a placeholder in our number system and represents the absence of quantity. Unlike counting numbers, zero signifies no value and is crucial for performing arithmetic operations, particularly in subtraction and indicating starting points. For instance, the temperature at which water freezes is 0°C, highlighting zero’s role in measurement scales.
Natural numbers, also known as counting numbers, are the set of positive integers starting from 1 and moving upwards infinitely (1, 2, 3, …). They do not include zero or any fractional, decimal, or negative numbers.
Examples: 1, 2, 3, 100, 101
Whole numbers include all natural numbers along with zero (0, 1, 2, 3, …). They are used in counting and do not include fractions or decimals.
Examples: 0, 1, 2, 50, 60
Integers encompass all whole numbers and their negative counterparts (… -3, -2, -1, 0, 1, 2, 3, …). They can represent quantities above or below zero.
Examples: -5, -4, 0, 10, 15
Rational numbers are any numbers that can be expressed as the quotient or fraction of two integers, where the denominator is not zero. They can be positive, negative, or zero.
Examples: 1/2, -3/4, 0.75 (since 0.75 = 3/4)
Irrational numbers cannot be expressed as a simple fraction or quotient of two integers. They have non-repeating, non-terminating decimal expansions.
Examples: ?2, ? (Pi), e (Euler’s number)
Description: Real numbers include all rational and irrational numbers, covering all possible magnitudes and including zero. They can represent any value along the number line.
Examples: -?3, 0, 4/5, ?5, ?
Complex numbers consist of a real part and an imaginary part and are represented as a + bi, where “a” and “b” are real numbers, and “i” is the square root of -1.
Examples: 2 + 3i, -1 + 2i
Prime numbers are natural numbers greater than 1 that have no divisors other than 1 and themselves.
Examples: 2, 3, 5, 7, 11
Composite numbers are natural numbers greater than 1 that are not prime, meaning they have divisors other than 1 and themselves.
Examples: 4, 6, 8, 9, 10
This classification highlights the diversity within the world of numbers, each type with its own unique properties and applications in various fields of mathematics and science.
| Number | In Words | Number | In Words |
|---|---|---|---|
| 1 | One | 11 | Eleven |
| 2 | Two | 12 | Twelve |
| 3 | Three | 13 | Thirteen |
| 4 | Four | 14 | Fourteen |
| 5 | Five | 15 | Fifteen |
| 6 | Six | 16 | Sixteen |
| 7 | Seven | 17 | Seventeen |
| 8 | Eight | 18 | Eighteen |
| 9 | Nine | 19 | Nineteen |
| 10 | Ten | 20 | Twenty |
| 21 | Twenty-One | 31 | Thirty-One |
| 22 | Twenty-Two | 32 | Thirty-Two |
| 23 | Twenty-Three | 33 | Thirty-Three |
| 24 | Twenty-Four | 34 | Thirty-Four |
| 25 | Twenty-Five | 35 | Thirty-Five |
| 26 | Twenty-Six | 36 | Thirty-Six |
| 27 | Twenty-Seven | 37 | Thirty-Seven |
| 28 | Twenty-Eight | 38 | Thirty-Eight |
| 29 | Twenty-Nine | 39 | Thirty-Nine |
| 30 | Thirty | 40 | Forty |
| 41 | Forty-One | 51 | Fifty-One |
| 42 | Forty-Two | 52 | Fifty-Two |
| 43 | Forty-Three | 53 | Fifty-Three |
| 44 | Forty-Four | 54 | Fifty-Four |
| 45 | Forty-Five | 55 | Fifty-Five |
| 46 | Forty-Six | 56 | Fifty-Six |
| 47 | Forty-Seven | 57 | Fifty-Seven |
| 48 | Forty-Eight | 58 | Fifty-Eight |
| 49 | Forty-Nine | 59 | Fifty-Nine |
| 50 | Fifty | 60 | Sixty |
| 61 | Sixty-One | 71 | Seventy-One |
| 62 | Sixty-Two | 72 | Seventy-Two |
| 63 | Sixty-Three | 73 | Seventy-Three |
| 64 | Sixty-Four | 74 | Seventy-Four |
| 65 | Sixty-Five | 75 | Seventy-Five |
| 66 | Sixty-Six | 76 | Seventy-Six |
| 67 | Sixty-Seven | 77 | Seventy-Seven |
| 68 | Sixty-Eight | 78 | Seventy-Eight |
| 69 | Sixty-Nine | 79 | Seventy-Nine |
| 70 | Seventy | 80 | Eighty |
| 81 | Eighty-One | 91 | Ninety-One |
| 82 | Eighty-Two | 92 | Ninety-Two |
| 83 | Eighty-Three | 93 | Ninety-Three |
| 84 | Eighty-Four | 94 | Ninety-Four |
| 85 | Eighty-Five | 95 | Ninety-Five |
| 86 | Eighty-Six | 96 | Ninety-Six |
| 87 | Eighty-Seven | 97 | Ninety-Seven |
| 88 | Eighty-Eight | 98 | Ninety-Eight |
| 89 | Eighty-Nine | 99 | Ninety-Nine |
| 90 | Ninety | 100 | One Hundred |
A number series is a sequence of numbers following a particular pattern or rule. These series are foundational in understanding mathematical concepts and appear frequently in various mathematical studies, including arithmetic progressions, geometric progressions, and Fibonacci sequences.
1. Cardinal Numbers: Cardinal numbers indicate the quantity of items in a set, such as one, five, ten, etc., quantifying elements in a collection.
2. Ordinal Numbers: Ordinal numbers denote the position or order of items within a sequence, like first, second, third, fourth, etc., specifying rank or sequence.
3. Nominal Numbers: Nominal numbers serve as identifiers or labels without indicating quantity or order, essentially naming or tagging objects without implying numerical value.
4. Pi (?): Pi, approximately 3.14159, is a crucial mathematical constant representing the ratio of a circle’s circumference to its diameter, symbolizing the relationship between the two.
5. Euler’s Number (e): Euler’s number, around 2.7182818, stands as a fundamental irrational number in mathematics, forming the base of natural logarithms and playing a key role in various mathematical contexts.
6. Golden Ratio (?): The golden ratio, roughly 1.618, is an irrational number without a repeating pattern, known for its aesthetic significance in art and architecture, as well as its occurrence in nature and geometry.
Numbers exhibit various properties that are fundamental to arithmetic and algebra. Below are some key properties along with examples to illustrate their application:
This property states that changing the order of numbers in an operation does not change the result.
According to this property, the way numbers are grouped in an operation does not affect the outcome.
This property shows how multiplication is distributed over addition or subtraction.
The identity property states that there is an identity element for each operation that, when applied, does not change the number.
This property indicates that each number has an inverse that, when combined with the original number using an operation, returns the identity element of that operation.
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself.
A composite number is a positive integer greater than 1 that is not prime, meaning it has at least one divisor other than 1 and itself.
Understanding these properties helps in the simplification of mathematical expressions and in solving various mathematical problems more efficiently.
Pre-number math encompasses foundational mathematical concepts taught before introducing formal numbers. It includes understanding shapes, sizes, patterns, and basic counting skills. These concepts are crucial for young learners, as they lay the groundwork for recognizing quantities and developing early arithmetic skills. Activities like sorting objects by color or shape and simple counting games are examples of pre-number math, helping children grasp the basic idea of quantities and relationships between objects.
Number names are the words used to represent numbers. Teaching number names is essential in bridging the gap between the abstract concept of numbers and their practical use. This includes understanding both the cardinal numbers (one, two, three, etc.) that denote quantity and the ordinal numbers (first, second, third, etc.) that indicate position. Number names help in enhancing numerical literacy, allowing individuals to communicate and understand quantities and positions in everyday life.
PEMDAS is an acronym that stands for Parentheses, Exponents, Multiplication and Division (from left to right), Addition and Subtraction (from left to right). It is a mnemonic that helps remember the order of operations in mathematics, ensuring that mathematical expressions are solved correctly and consistently. For example, in the expression 2+3×4, multiplication is performed before addition, resulting in 14, not 20. PEMDAS is fundamental in ensuring accuracy in solving equations and mathematical problems.
Number systems encompass the various ways in which numbers can be organized and represented, catering to different mathematical operations and concepts. These include the familiar decimal system, binary system, and complex numbers, among others, each serving specific roles in mathematics, computing, and science.
| Feature | Cardinal Numbers | Ordinal Numbers |
|---|---|---|
| Definition | Indicate the quantity of items in a set. | Denote the position or order of items within a sequence. |
| Purpose | Used to count how many objects are present. | Used to specify the rank or sequence of objects. |
| Example | Three apples, indicating the count of apples. | Third place in a race, indicating the position. |
| Representation | Represented by numbers like 1, 2, 3… | Represented by first, second, third… |
| Use in Sentences | “I have two dogs.” | “She finished in second place.” |
Consecutive numbers are numbers that follow each other in order, with a difference of one between each pair. For example, 4, 5, and 6 are consecutive because each number is one more than the number before it.
Integers encompass the set of whole numbers including positive numbers, negative numbers, and zero. This category includes numbers like -3, 0, 1, and 2, but excludes fractions and decimals.
Co-prime numbers, also known as relatively prime numbers, are two numbers that have no common factors other than 1. For instance, 8 and 15 are co-prime because their only common divisor is 1.
A perfect number is a positive integer that is equal to the sum of its proper divisors, excluding itself. The smallest perfect number is 6, which is the sum of its divisors 1, 2, and 3.
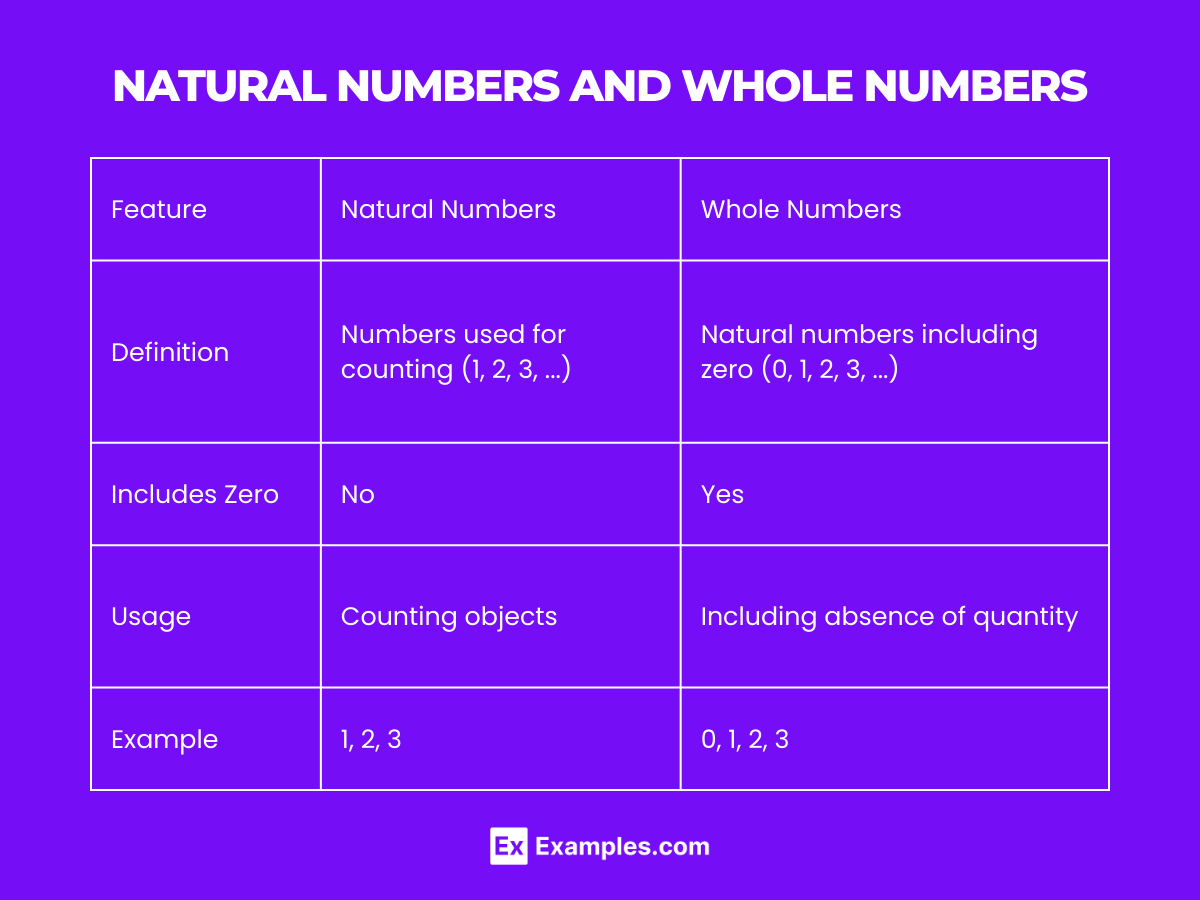
| Feature | Natural Numbers | Whole Numbers |
|---|---|---|
| Definition | Numbers used for counting (1, 2, 3, …) | Natural numbers including zero (0, 1, 2, 3, …) |
| Includes Zero | No | Yes |
| Usage | Counting objects | Including absence of quantity |
| Example | 1, 2, 3 | 0, 1, 2, 3 |
| Feature | Even Numbers | Odd Numbers |
|---|---|---|
| Divisibility | Divisible by 2 | Not divisible by 2 |
| Last Digit | 0, 2, 4, 6, 8 | 1, 3, 5, 7, 9 |
| Examples | 2, 4, 6 | 1, 3, 5 |
| Feature | Prime Numbers | Composite Numbers |
|---|---|---|
| Divisors | Exactly two distinct divisors: 1 and itself | More than two divisors |
| Examples | 2, 3, 5 | 4, 6, 8 |
| Factorization | Cannot be factorized into other numbers | Can be factorized into smaller numbers |
| Feature | Fractions | Decimals |
|---|---|---|
| Representation | Expressed as a ratio of two integers | Expressed in base 10, representing a part of whole |
| Example | 1/2, 3/4 | 0.5, 0.75 |
| Division | Represents division | Result of division |
| Feature | Rational Numbers | Irrational Numbers |
|---|---|---|
| Definition | Can be expressed as a fraction of two integers | Cannot be fully expressed as a fraction |
| Decimal Expansion | Terminating or repeating | Non-terminating, non-repeating |
| Examples | 1/2, -3/4 | ?, ?2 |
Real numbers encompass all the numbers on the number line, including both rational numbers (such as fractions and whole numbers) and irrational numbers (those that cannot be expressed as a fraction). This set forms the foundation of continuous mathematics, applicable in measuring and quantifying real-world quantities and phenomena.
Complex numbers extend beyond real numbers by including a real part and an imaginary part (multiplied by the imaginary unit i, where i2= -1). This allows for the representation and solution of equations that no real number can solve, playing a crucial role in advanced mathematics, engineering, and physics.
Factors of a number are integers that divide into it without leaving a remainder, essentially the building blocks from which the number is constructed. For example, the factors of 6 are 1, 2, 3, and 6. Multiples of a number are obtained by multiplying that number by an integer. For instance, the first few multiples of 3 are 3, 6, 9, 12, etc. Understanding factors and multiples is vital for exploring divisibility, prime factorization, and the Least Common Multiple (LCM) and Greatest Common Divisor (GCD) of numbers.
The Highest Common Factor (HCF), also known as the Greatest Common Divisor (GCD), is the largest number that divides two or more numbers without leaving a remainder. It’s crucial for simplifying fractions to their lowest terms.
Examples:
The Least Common Multiple (LCM) of two or more numbers is the smallest number that is a multiple of all the numbers. It’s used in adding or subtracting fractions with different denominators.
Examples:
Prime Factorization is breaking down a number into the set of prime numbers which, when multiplied together, give the original number. It’s fundamental for finding the LCM and HCF of numbers.
Examples:
These concepts of HCF, LCM, and Prime Factorization are foundational in mathematics, serving various applications in solving problems related to fractions, number theory, and arithmetic operations.
Question: If there are 7 apples in a basket and you add 5 more, how many apples are there in total?
Solution:
Question: In a race, if John finishes before Mike and Mike finishes before Sam, who finishes second?
Solution:
Question: If a soccer player’s jersey number is 10, does it indicate his team’s score or position?
Solution:
Question: What is the approximate circumference of a circle with a diameter of 7 units?
Solution:
Question: Calculate the value of an investment that grows at a rate of 100% per year (continuously compounded) for 1 year with an initial investment of $1.
Solution:
Question: If the length of a rectangle is ? times larger than its width and the width is 8 units, what is the length?
Solution:
These examples demonstrate practical applications and the inherent beauty of numbers, showcasing their relevance across various contexts.
In conclusion, our exploration into the realm of numbers, from the basic cardinal, ordinal, and nominal classifications to the complex concepts of pi, Euler’s number, and the golden ratio, unveils the rich tapestry of mathematics. This guide aims to illuminate the intricate beauty and utility of numbers, equipping educators with the knowledge to inspire a deeper understanding and appreciation of mathematics among students. Through clear examples and engaging explanations, we endeavor to make mathematics an accessible and fascinating subject for learners at all levels.
Text prompt
Add Tone
Types of Numbers
Numbers in Words
Which number is both rational and real?
4
π
i
√2
Identify the complex number in the following set: { 2, −1 , 3i, √4 }.
2
-1
3i
√4
Which of the following numbers is a prime number?
9
15
17
21
Which of the following numbers is not a prime number?
2
3
4
5
Which of the following sets represents natural numbers?
{ -1, 0, 1, 2 }
{ 0, 1, 2, 3 }
{ 1, 2, 3, 4 }
{ -2, -1, 0, 1 }
Which of the following is an example of an integer that is not a whole number?
-3
0
2
4
Which of the following numbers can be expressed as a ratio of two integers?
√5
π
8/3
e
Which of the following numbers is irrational?
7/8
π
0.5
22/7
Which of the following is an example of a complex number?
5
√7
3−2i
π
Which number is both a square and a cube?
64
68
72
76
Before you leave, take our quick quiz to enhance your learning!

