Prime Number – Examples, Properties, Types, Rules
Prime numbers, the building blocks of mathematics. This guide is meticulously crafted to demystify the concept of primes, presenting them through engaging examples that resonate with both educators and students. Designed to make math both accessible and enjoyable, it breaks down the essence of prime numbers using straightforward English. Ideal for classroom instruction, this resource aims to illuminate the unique properties of primes, encouraging a deeper understanding and appreciation of their role in number theory and beyond.
What are Prime Numbers – Definition
Prime numbers are natural numbers greater than 1 that have exactly two distinct positive divisors: 1 and themselves. This means they cannot be evenly divided by any other numbers. Primes are fundamental in mathematics due to their role in various number properties and operations, serving as the “atoms” of the numerical world.
What is the Best Example of Prime Numbers?
The Significance of 2
The number 2 is often heralded as the best example of a prime number because it is the only even prime number. All other even numbers can be divided by 2, making them composite. The uniqueness of 2 highlights the diversity within the prime numbers and its foundational role in the structure of mathematics. It serves as a gateway to understanding the concept of primality and its implications for divisibility, factors, and the broader universe of numbers.
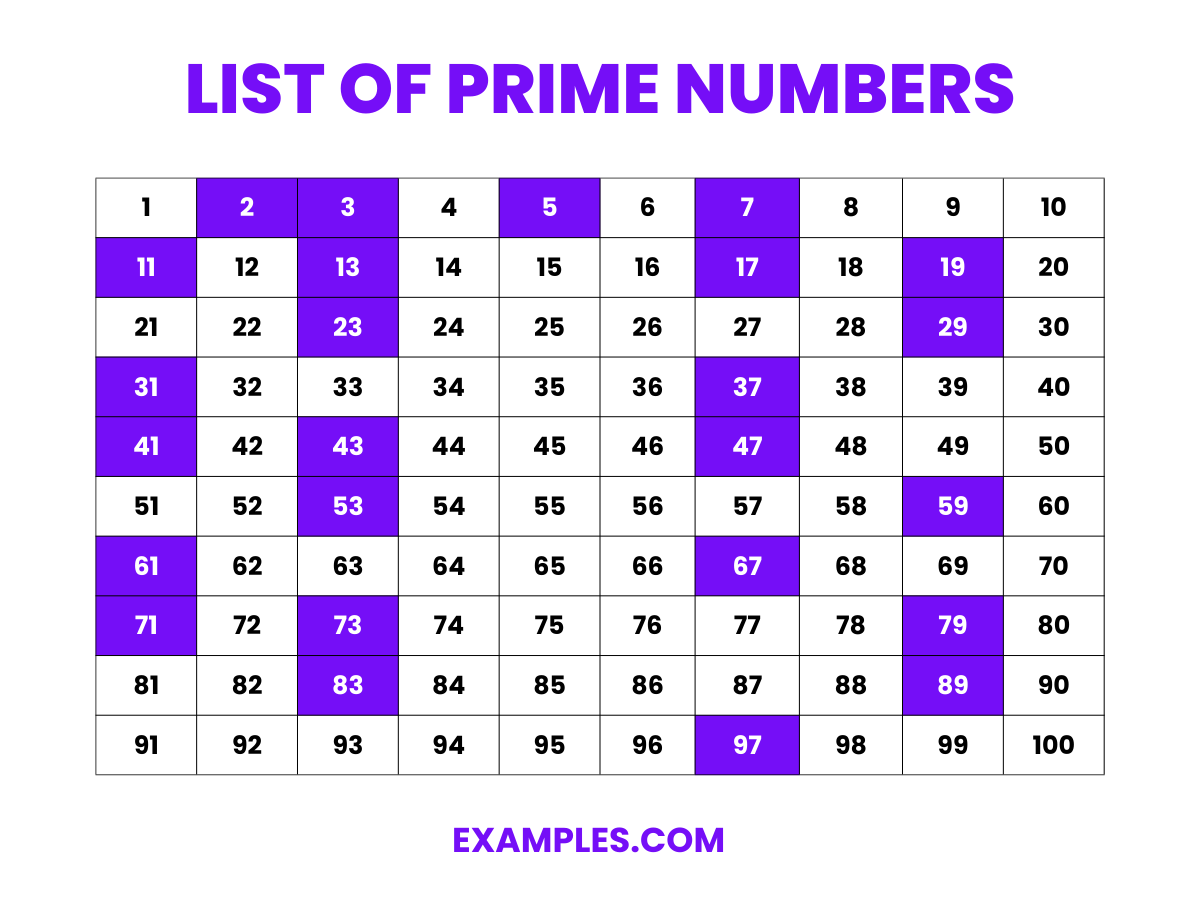
List of Prime Numbers
Unlock the enigmatic world of prime numbers, those unique integers greater than 1 that are divisible only by 1 and themselves. This fascinating concept is a cornerstone of mathematics, pivotal for understanding the fundamentals of number theory, cryptography, and complex problem-solving. Our guide, rich with examples, is crafted to demystify primes for educators and students alike, making this key mathematical concept accessible, engaging, and easy to grasp. Through our tailored explanations, learn how prime numbers not only underpin the structure of mathematics but also how they’re used in real-world applications, enhancing lessons with a blend of theory and practicality.
List of Prime Numbers from 1 -1000
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997.
Types of Prime Numbers
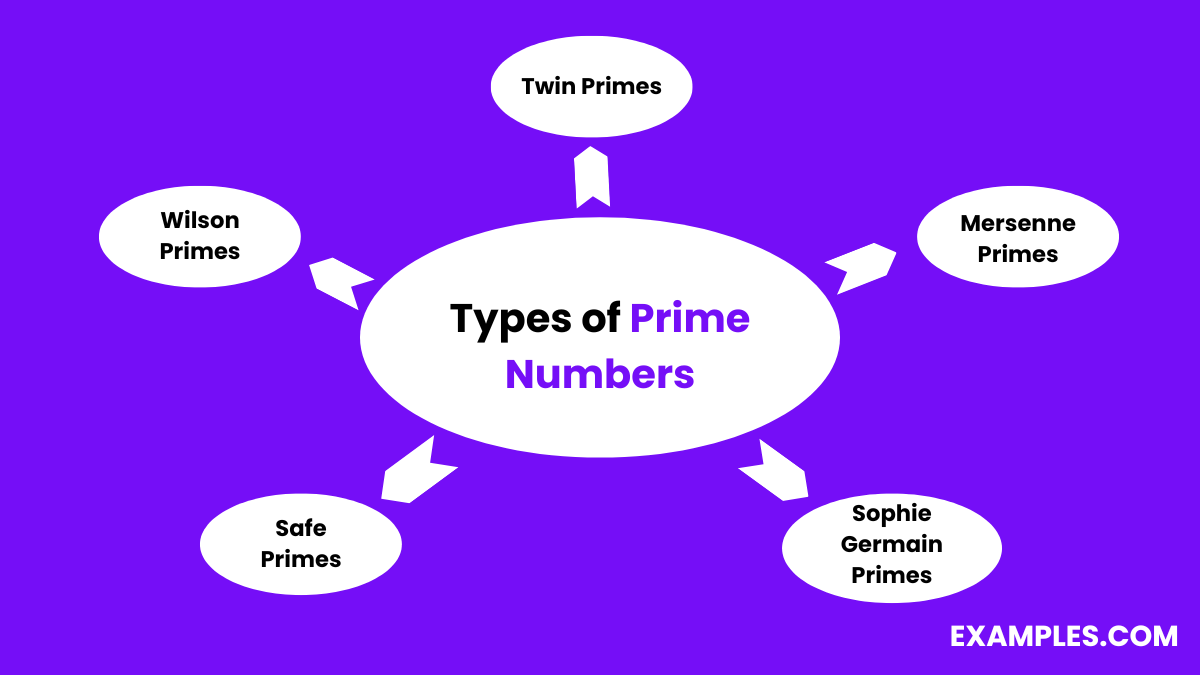
Prime numbers, the indivisible anchors of mathematics, come in various intriguing types, each with unique characteristics and roles in number theory. From twin primes that stand close to each other to mysterious Mersenne primes powering cryptography, understanding these types enriches our grasp of mathematical fundamentals. This exploration not only fascinates educators and students but also lays a foundation for advanced mathematical concepts, showcasing the endless wonders hidden within prime numbers.
Examples
- Twin Primes
- Pairs of primes separated by a single number, like (11, 13).
- Explanation: Highlight the close relationship between certain primes, sparking curiosity about their distribution.
- Mersenne Primes
- Primes of the form 2p−1, where p is also prime, like 31 ( 25−1 ) .
- Explanation: Essential in cryptography, showcasing the intersection of prime numbers and computer science.
- Sophie Germain Primes
- Primes where is also prime, like 11 since 2∗11+1 = is prime.
- Explanation: Play a crucial role in cryptography and prime research, emphasizing the depth of prime number theory.
- Safe Primes
- Primes where is also prime, like 23 since 23−1/2 1 = is prime.
- Explanation: Important in cryptographic algorithms for their robust properties.
- Wilson Primes
- Primes where ( p-1 ) ! + is divisible by p2, like 13.
- Explanation: Rare and peculiar, Wilson primes underscore the fascinating complexities within prime numbers.
Classification of Prime Numbers
Prime numbers are classified into distinct categories based on their specific attributes and relationships. This classification helps mathematicians understand the intricate fabric of the numerical universe, driving forward both theoretical research and practical applications. For teachers and students, delving into these classifications reveals the organized complexity of prime numbers, enhancing mathematical literacy and sparking interest in deeper mathematical exploration.
Examples
- Regular Primes
- Primes that do not divide the class number of the th cyclotomic field, like 3.
- Explanation: Offer insights into advanced number theory, connecting primes to field properties.
- Cuban Primes
- Primes expressed as the difference between two consecutive cubes, like 7 ( 23-13).
- Explanation: Illustrate geometric interpretations of prime numbers, linking algebra with geometry.
- Fermat Primes
- Primes of the form 2212.+1, like 17 ( 2212.+1 )
- Explanation: Fundamental in constructing regular polygons with a compass and straightedge, blending geometry with number theory.
- Eisenstein Primes
- Primes in the Eisenstein integers without an imaginary part, like 5.
- Explanation: Bridge the gap between number theory and complex algebra, expanding the realm of prime numbers.
- Pierpont Primes
- Primes of the form 2u3u+1 ( 22*30+1 ).
- Explanation: Useful in certain constructions of regular polygons, showing the practical applications of prime numbers.
Set of Prime Numbers
The set of prime numbers, an infinite collection of fundamental mathematical entities, underpins the structure of the number system. This set, ranging from 2, the smallest prime, to numbers beyond imagination, is central to various fields of mathematics and its applications. Teachers introducing this concept to students open a gateway to understanding the building blocks of arithmetic, fostering a sense of wonder and inquiry into the patterns and theorems that define the universe of numbers.
Examples
- The First Five Primes
- 2, 3, 5, 7, 11.
- Explanation: Serve as the introductory foundation to the concept of primality, illustrating the basic properties of prime numbers.
- Primes Less Than 100
- Highlighting primes like 29, 41, 59, and 97.
- Explanation: Offer a broader view of prime distribution, showing students the variability and density of primes.
- Centennial Primes
- Primes around 100, such as 101 and 103.
- Explanation: Transition to larger primes, challenging students to consider the infinite nature of prime numbers.
- Millennium Primes
- Large primes such as 1009 and 1013.
- Explanation: Push the boundary of prime exploration, introducing students to primes in the thousands.
- Titanic Primes
- Extremely large primes, often found through computational methods.
- Explanation: Demonstrate the modern quest for finding large primes, combining mathematics with computer science.
Prime Numbers on a Number Line
Visualizing prime numbers on a number line illuminates their distribution across the numerical spectrum, offering a unique perspective on their spacing and frequency. This approach aids in understanding the concept of primality by placing primes in direct relation to composite numbers, enhancing learners’ ability to identify and work with these fundamental building blocks of mathematics. It’s an effective teaching tool that encourages exploration and pattern recognition, making it an invaluable resource for educators and students delving into number theory.
Examples
- Marking Primes up to 10
- On a number line, primes under 10 (2, 3, 5, 7) are highlighted. This shows early prime distribution.
- Use: Introduces the concept of prime numbers and their identification.
- Highlighting Primes up to 20
- Extending the line to include primes up to 20 (11, 13, 17, 19) demonstrates increasing prime gaps.
- Use: Teaches about the irregular spacing between prime numbers.
- First 10 Primes
- Marking the first 10 primes on a number line gives a visual sense of prime density in initial numbers.
- Use: Helps understand how prime numbers become less frequent as numbers increase.
- Primes between 50 and 70
- Highlighting primes in this range shows the concept of prime deserts—areas where primes are less frequent.
- Use: Illustrates how prime numbers are distributed unevenly across larger numbers.
- Twin Primes Highlight
- Twin primes (e.g., 11 and 13, 17 and 19) are marked closely together, showing their special relationship.
- Use: Introduces the concept of twin primes and their proximity on the number line.
Graphing Prime Numbers on a Number Line
Graphing prime numbers on a number line not only visualizes their distribution but also introduces learners to the concept of mathematical patterns and anomalies. This graphical representation is a powerful tool for engaging students with the abstract idea of primality, making it tangible and fostering a deeper interest in the exploration of number theory. By graphing primes, educators can facilitate a more interactive learning experience, encouraging students to discover the unique properties of primes firsthand.
Examples
- Primes Under 50
- Graphing primes under 50 on a number line visually emphasizes the decreasing density of primes as numbers increase.
- Use: Demonstrates the basic principle that primes become less common as numbers get larger.
- Highlighting Consecutive Primes
- By graphing consecutive primes, students can visually appreciate the concept of prime gaps and their variability.
- Use: Enhances understanding of the unpredictable gaps between successive prime numbers.
- Sieving Primes
- Using a sieve method on a number line, like the Sieve of Eratosthenes, visually removes non-primes, leaving only primes.
- Use: Teaches historical and practical methods for finding prime numbers.
- Prime Clusters
- Identifying clusters of primes within specific ranges on a number line helps illustrate the concept of prime-rich areas.
- Use: Encourages exploration of patterns and anomalies within the distribution of prime numbers.
- Visualizing Prime Deserts
- Graphing a wider range on a number line to showcase areas with fewer primes, known as prime deserts.
- Use: Demonstrates the uneven distribution of prime numbers and introduces the concept of prime deserts.
Prime Numbers Operations
Operations with prime numbers are foundational in various fields of mathematics, including algebra and number theory. Understanding these operations enhances problem-solving skills and provides insight into the structure of the number system. For students and educators, exploring prime numbers operations is essential for developing a comprehensive understanding of mathematical concepts and their applications in real-world scenarios.
Examples
- Prime Addition
- Adding two primes to get a composite number, except when adding twin primes like 3 and 5 to get 8.
- Use: Shows that the sum of most prime pairs is composite, highlighting the uniqueness of twin primes.
- Prime Subtraction
- Subtracting a smaller prime from a larger often results in a composite, but can yield a prime difference.
- Use: Encourages investigation into the results of prime subtraction and its patterns.
- Multiplying Primes
- Multiplying two primes always results in a unique composite number with those primes as its only factors.
- Use: Demonstrates the fundamental theorem of arithmetic through prime factorization.
- Prime Division
- Dividing one prime number by another is impossible to do evenly, except by 1 or the prime itself.
- Use: Reinforces the concept of primes having only two divisors: 1 and the prime number itself.
- Prime Exponents
- Raising a prime number to any power results in a composite number with a unique prime factorization.
- Use: Illustrates the power of prime numbers in creating complex numbers through simple operations.
Addition of Prime Numbers
Exploring the addition of prime numbers unveils fascinating patterns and insights, crucial for students mastering arithmetic and number theory. This exploration enhances understanding of how these unique numbers interact, laying a foundation for advanced mathematical concepts and problem-solving skills. Ideal for educational settings, it encourages a deeper appreciation of prime numbers’ properties and their applications.
Examples
- Sum of Two Primes
- Adding two primes, like 2 and 5, gives 7, another prime. This simple addition showcases how primes can combine to form another prime or a composite number.
- Twin Primes Addition
- Twin primes, such as 11 and 13, when added (24), demonstrate that the sum of twin primes is always even, except for 3 and 5.
- Consecutive Primes Addition
- Adding consecutive primes like 17 and 19 results in 36, illustrating that their sum often leads to a composite number.
- Sum of Prime and Composite
- Adding a prime number to a composite, for instance, 7 (prime) and 4 (composite), results in 11, showing how prime properties influence addition outcomes.
- Adding Prime to Itself
- Doubling a prime number, such as adding 23 to itself, yields 46, always resulting in an even composite number.
Rules of Prime Numbers in Addition
Addition involving prime numbers follows unique patterns, offering insights into their behavior. These rules are instrumental for students to understand the inherent properties of primes and their significance in arithmetic operations.
Substraction of Prime Numbers
Subtraction of prime numbers involves taking the difference between two prime numbers, just like any other subtraction process. However, the outcome of subtracting prime numbers can lead to various interesting observations and results, which can be particularly intriguing in the study of number theory and mathematics education.
Key Points in Subtraction of Prime Numbers:
- Result May or May Not Be Prime: The difference between two prime numbers is not necessarily a prime number. For example, subtracting 3 from 5 gives 2, which is prime, but subtracting 11 from 17 gives 6, which is not prime.
- Even and Odd Outcomes: If you subtract a smaller prime from a larger prime and both are odd (as all primes greater than 2 are), the result will always be even. This is because the subtraction of two odd numbers yields an even number.
- Prime Gaps: The result of subtracting one prime number from another can demonstrate the concept of prime gaps, which are the differences between successive prime numbers. These gaps can vary widely as numbers increase.
- Potential for Negative Results: If a larger prime number is subtracted from a smaller prime number, the result will be negative. While negative numbers are not considered prime, this operation highlights the importance of order in subtraction.
- Special Cases: The subtraction of the same prime number from itself, such as 7 – 7, will always result in 0, which is neither prime nor composite.
Examples of Prime Number Subtraction:
- Subtracting Small Primes:
- 5 – 2 = 3. Both the operands and the result are prime numbers.
- Subtracting Larger Primes:
- 19 – 11 = 8. This subtraction involves larger primes and yields a non-prime result.
- Subtracting Consecutive Primes:
- 17 – 13 = 4. Demonstrates a small prime gap of 4, yielding a non-prime even number.
- Subtracting with Negative Result:
- 3 – 5 = -2. Shows that subtraction of a larger prime from a smaller yields a negative number.
- Subtracting Same Primes:
- 11 – 11 = 0. Results in 0, illustrating the identity property of subtraction.
Understanding the subtraction of prime numbers offers valuable insights into the behavior of numbers and the foundational principles of arithmetic. It enriches students’ mathematical knowledge and encourages them to explore more complex concepts within the realm of primes and number theory.
Rules of Prime Numbers in Subtraction
Subtracting prime numbers can reveal interesting relationships and patterns. These rules help demystify how primes interact, providing a deeper understanding of their distinct characteristics.
Multiplication of Prime Numbers
Multiplication involving prime numbers opens a window to exploring fundamental principles of arithmetic and number theory. This concept is pivotal in understanding the building blocks of numbers, enhancing students’ mathematical skills and knowledge.
Examples
- Product of Two Primes
- Multiplying two primes, like 3 and 7, gives 21, illustrating how the product is always a composite number.
- Multiplying a Prime by Itself
- Squaring a prime, such as 5, results in 25, demonstrating that primes can generate square numbers.
- Prime Times Composite
- Multiplying a prime by a composite, for instance, 2 (prime) by 6 (composite), results in 12, showing multiplication’s role in generating larger composites.
- Product of Consecutive Primes
- The product of consecutive primes, such as 2 and 3, yields 6, emphasizing the concept of prime factorization.
- Multiplying Twin Primes
- Multiplying twin primes, like 11 and 13, results in 143, showcasing how unique prime products can be.
Rules of Prime Numbers in Multiplication
The multiplication of prime numbers follows specific rules that highlight their unique properties and the fundamental theorem of arithmetic. Understanding these rules is crucial for grasping the essence of prime numbers and their role in number theory.
Division of Prime Numbers
Division involving prime numbers offers a profound insight into the indivisibility of primes and their foundational role in the structure of mathematics. This aspect is essential for students to comprehend the unbreakable nature of primes and their applications.
Examples
- Dividing Prime by Prime
- Dividing a prime by another prime, such as 13 by 2, results in a fraction, underscoring primes’ indivisibility.
- Prime Divided by Composite
- A prime number divided by a composite, like 7 divided by 4, also results in a fraction, highlighting the prime’s inability to be evenly divided by non-factors.
- Composite Divided by Prime
- Dividing a composite number by a prime factor, for example, 15 by 5, results in another prime (3), illustrating prime factorization.
- Division Leading to Whole Number
- When a prime divides a product of primes (like 2 dividing 2×3=6), the quotient is another whole number, demonstrating how primes distribute over multiplication.
- Dividing a Prime by 1 or Itself
- Dividing a prime by 1 or itself always results in a whole number, reinforcing the definition of prime numbers.
Rules of Prime Numbers in Division
The division involving prime numbers is governed by rules that reinforce their fundamental properties, such as indivisibility by any number other than 1 and themselves. These rules are key for students to understand the unique characteristics of primes and their significance in mathematics.
Properties of Prime Numbers
Prime numbers, the indivisible building blocks of the numerical world, possess unique properties that make them a subject of endless fascination and study. This concise guide explores the inherent characteristics of primes, including their distribution, uniqueness, and the fundamental theorem of arithmetic, enriching mathematical understanding for teachers and students alike.
Examples
- Uniqueness
- Each prime number is distinct, having no divisors other than 1 and itself.
- Use: Fundamental in proving the uniqueness of prime factorization.
- Infinitude
- Primes are infinite, as demonstrated by Euclid’s proof.
- Use: Encourages exploration into the limitless nature of numbers and primes.
- Distribution
- Prime numbers become less frequent as numbers get larger, but they never stop appearing.
- Use: Introduces students to the concept of number density and distribution patterns.
- Twin Primes
- Pairs of primes that are two units apart, like (11, 13), show unique clustering.
- Use: Leads to discussions on prime conjectures and unsolved problems in mathematics.
- Goldbach’s Conjecture
- Every even number greater than 2 is proposed to be the sum of two primes.
- Use: Engages students with one of the most famous unsolved problems in number theory.
How to Represent Prime Numbers on a Number Line?
Representing prime numbers on a number line is a visual and intuitive method that helps illustrate their distribution and the concept of primality. This approach is invaluable in education, making the abstract nature of primes more tangible and comprehensible for students. It visually demarcates primes and offers insights into their patterns and spacing, enhancing mathematical curiosity and understanding.
Examples
- Marking Primes
- Place a mark or dot above each prime number on a horizontal line.
- Use: Visually distinguishes primes from composites, emphasizing their distribution.
- Highlighting Twin Primes
- Special markers can denote twin primes, illustrating their close proximity.
- Use: Helps students identify and understand the concept of twin primes.
- Using Colors
- Different colors can represent primes of different forms, like safe primes or Sophie Germain primes.
- Use: Facilitates deeper exploration into subclasses of prime numbers.
- Gaps Between Primes
- Noting the increasing gaps between consecutive primes on the line.
- Use: Introduces students to the idea of prime gaps and their significance.
- Prime Clusters
- Clusters of primes can be highlighted to show areas of higher density.
- Use: Demonstrates the non-uniform distribution of primes along the number line.
Applications of Prime Numbers
Prime numbers are not just theoretical constructs but have practical applications across various fields, from cryptography to natural phenomena modeling. This guide unveils the real-world utility of primes, illustrating how these fundamental numbers underpin modern technology, security systems, and scientific research, making them a fascinating study for educators and students alike.
Examples
- Cryptography
- Primes are crucial in encryption algorithms like RSA, securing digital communications.
- Use: Demonstrates the importance of primes in protecting information in the digital age.
- Random Number Generation
- Primes help generate sequences of random numbers for simulations and modeling.
- Use: Shows the application of primes in computer science and statistical modeling.
- Music Theory
- The relationship between prime numbers and musical harmonics influences instrument design.
- Use: Connects mathematical concepts with art, illustrating the interdisciplinary nature of primes.
- Coding Theory
- Primes are used in error detection and correction codes to ensure accurate data transmission.
- Use: Highlights the role of primes in reliable communication technologies.
- Quantum Computing
- Prime factorization is a challenge for classical computers but efficient on quantum models.
- Use: Engages students with the future of computing and primes’ role in advancing technology.
How to Find Prime Numbers?
Discovering prime numbers involves identifying natural numbers greater than 1 that are only divisible by 1 and themselves. This process, essential for mathematical exploration and application, can be simplified into manageable steps, enhancing the learning experience for students. Engaging with this method not only sharpens mathematical skills but also fosters a deeper appreciation for the elegance of number theory.
Steps
- Start with 2: The smallest prime number.
- Explanation: Begin your search with 2, acknowledging it as the only even prime.
- Use the Sieve of Eratosthenes: A classic method to filter primes.
- Explanation: Eliminate multiples of each prime number to uncover new primes.
- Test Divisibility: For numbers greater than 2, check divisibility by known primes.
- Explanation: If a number is not divisible by any prime number less than its square root, it’s prime.
- Check up to the Square Root: No need to test divisibility beyond a number’s square root.
- Explanation: A factor larger than the square root would necessitate a smaller counterpart that’s already been tested.
- Continue Sequentially: Move through numbers, applying these rules.
- Explanation: This systematic approach helps in identifying primes efficiently.
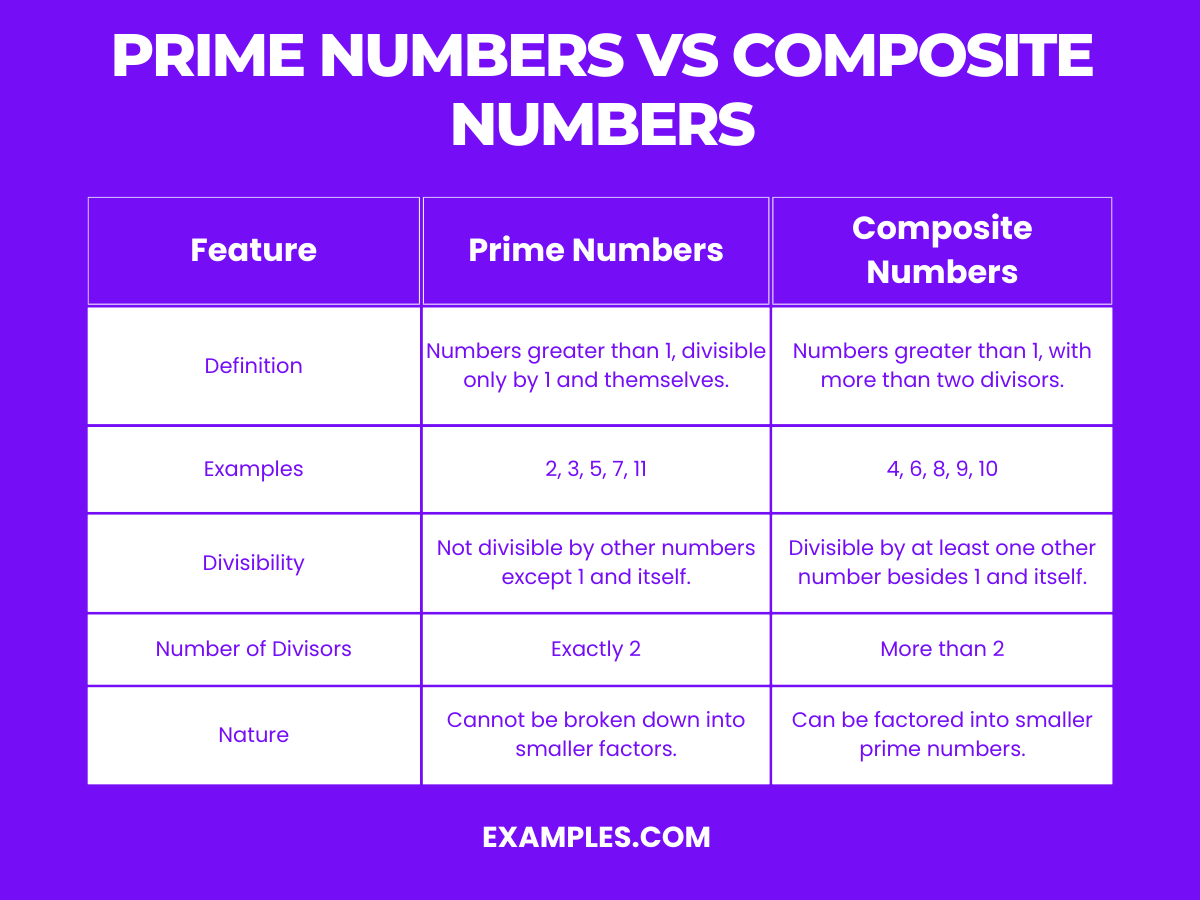
Prime Numbers vs Composite Numbers
Understanding the distinction between prime and composite numbers is pivotal, providing clarity on basic mathematical concepts. This comparison lays the groundwork for further exploration into number theory, primes, and their significant role in various mathematical applications.
| Feature | Prime Numbers | Composite Numbers |
|---|---|---|
| Definition | Numbers greater than 1, divisible only by 1 and themselves. | Numbers greater than 1, with more than two divisors. |
| Examples | 2, 3, 5, 7, 11 | 4, 6, 8, 9, 10 |
| Divisibility | Not divisible by other numbers except 1 and itself. | Divisible by at least one other number besides 1 and itself. |
| Number of Divisors | Exactly 2 | More than 2 |
| Nature | Cannot be broken down into smaller factors. | Can be factored into smaller prime numbers. |
In conclusion, prime numbers serve as the bedrock of mathematics, embodying simplicity and complexity in equal measure. This article has illuminated the methods to identify primes, and distinguished them from composite numbers, enriching the understanding of these fundamental concepts. Tailored for educators and students, it aims to demystify primes, encouraging a deeper engagement with mathematics and enhancing communication skills through the beauty of numbers.