Factors of 23

The factors of 23 is crucial in grasping fundamental mathematical concepts. Factors are numbers that can be multiplied together to yield another number. In the case of 23, the factors are quite simple due to its nature as a prime number. This means it can only be divided evenly by 1 and itself, with no other divisors. Recognizing the factors of 23 helps in various applications, from simplifying fractions to solving equations. This guide will delve into what makes 23 a prime number, its positive and negative factors, and their significance in mathematics.

What are the Factors of 23?

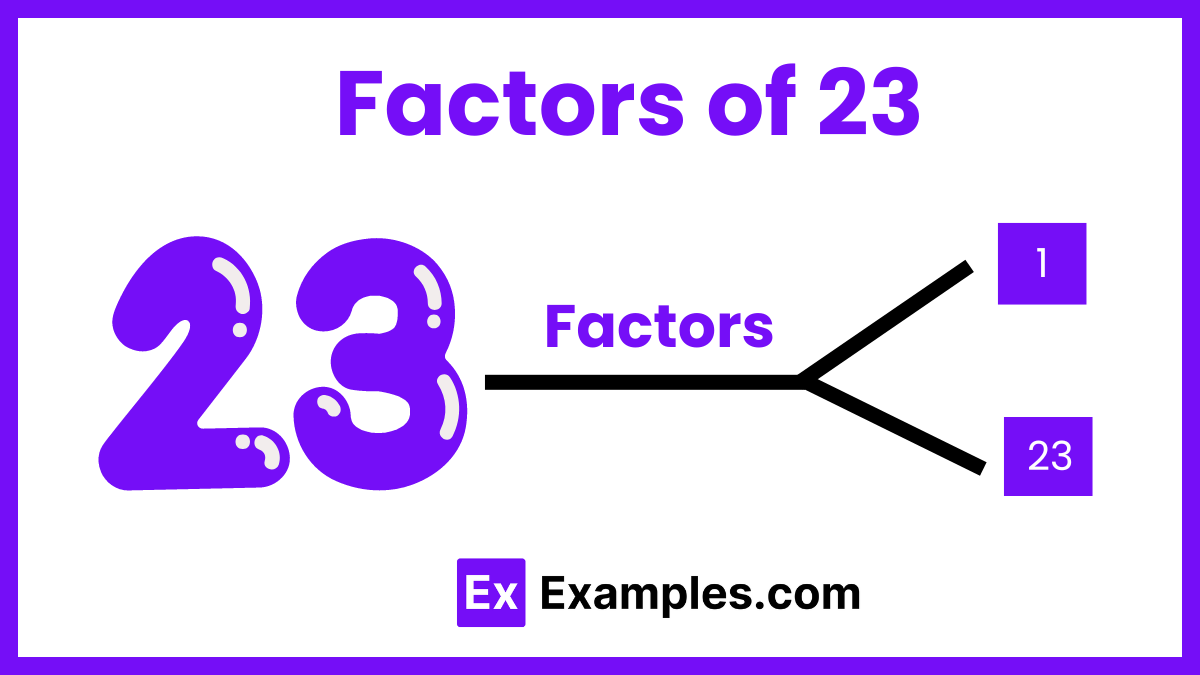
The factors of 23 are the numbers that divide 23 exactly without leaving a remainder. Since 23 is a prime number, it has only two factors: 1 and 23. This means that the only numbers that can be multiplied together to equal 23 are 1 × 23. There are no other pairs of factors for 23. Understanding that 23 is prime is important in various mathematical contexts, such as simplifying fractions and solving algebraic equations.

Factors Pairs of 23

• (1, 23): Multiplying 1 by 23 gives 23. This demonstrates that 1 and 23 are the only positive factors of 23.
• (-1, -23): Multiplying -1 by -23 also results in 23. This shows that the negative factor pairs of 23 include -1 and -23.

These pairs illustrate the limited factor pairs for 23, confirming its status as a prime number.

How to Calculate Prime Factors of 23?

Calculating the prime factors of a number involves breaking it down into its prime components. Prime numbers are those greater than 1 that have no divisors other than 1 and themselves. Since 23 is a prime number, its prime factorization is straightforward. Here’s how to determine the prime factors of 23:

Step 1: Identify if the number is a prime.

• Determine if 23 is a prime number by checking if it is divisible by any prime numbers smaller than itself.

Step 2: Test divisibility.

• Check if 23 is divisible by the smallest prime number, 2. Since 23 is odd, it is not divisible by 2.
• Next, check if 23 is divisible by 3. The sum of the digits (2 + 3 = 5) is not divisible by 3, so 23 is not divisible by 3.
• Continue this process with the next primes (5, 7, etc.) until you reach the square root of 23. Since 23 is not divisible by any of these, it remains indivisible.

Step 3: Conclude prime status.

• Since 23 is not divisible by any smaller prime numbers, it is confirmed to be a prime number itself.

Factors of 23 : Examples

Example 1: Identifying Factors

• Problem: List all the positive factors of 23.
• Solution: Since 23 is a prime number, its only positive factors are 1 and 23.

Example 2: Verifying Prime Status

• Problem: Show that 23 is a prime number.
• Solution: To verify, check divisibility by all prime numbers less than the square root of 23 (approximately 4.8). 23 is not divisible by 2, 3, or 5, confirming it is a prime number.

Example 3: Simplifying Fractions

• Problem: Simplify the fraction 46/23​.
• Solution: Since 23 is a factor of 46, divide both the numerator and denominator by 23:46÷23/23÷23=2/1=2

Example 4: Solving Word Problems

• Problem: If you have 23 candies and want to distribute them evenly among 23 children, how many candies will each child get?
• Solution: Divide the total number of candies by the number of children:23÷23=1 Each child gets 1 candy.

Example 5: Checking for Divisibility

• Problem: Determine if 69 is divisible by 23.
• Solution: Divide 69 by 23:69÷23=3 Since the quotient is an integer, 69 is divisible by 23.

Factors of 23 : Tips

The factors of 23 can aid in various mathematical tasks, especially given its nature as a prime number. Here are some helpful tips for working with the factors of 23:

• Identify Prime Status Early: Recognize that 23 is a prime number, meaning its only factors are 1 and 23. This simplifies many calculations.
• Use Simple Division: For factor identification, quickly divide 23 by smaller prime numbers (2, 3, 5, etc.). Since it’s not divisible by any of these, it’s confirmed as a prime.
• Apply Prime Factorization: Remember that the prime factorization of 23 is simply 23 itself. This is useful in problems requiring prime factors.
• Simplify Fractions Easily: When simplifying fractions with 23 in the numerator or denominator, knowing it’s prime helps determine that 23 can only simplify with another 23.
• Check Divisibility Quickly: To check if a number is divisible by 23, divide and see if the result is an integer.
• Recognize Factor Pairs: For 23, the factor pairs are straightforward: (1, 23) and (-1, -23). This is useful in problems requiring factor pairs.
• Utilize in Word Problems: Apply the knowledge that 23 has limited factors in distribution problems, ensuring accurate and efficient solutions.
• Mathematical Applications: Use the prime nature of 23 to solve problems in algebra, number theory, and other mathematical areas where prime factorization is relevant.

What is the prime factorization of 23?

The prime factorization of 23 is simply 23 itself, as it is a prime number and cannot be divided by any other numbers except 1 and 23.

How can I verify that 23 is a prime number?

To verify that 23 is a prime number, check its divisibility by all prime numbers less than its square root (approximately 4.8). Since 23 is not divisible by 2, 3, or 5, it is confirmed to be prime.

What is the greatest common factor (GCF) of 23 and any other number?

A16: The GCF of 23 and any other number is either 1 (if the other number is not a multiple of 23) or 23 (if the other number is a multiple of 23).

Is 23 a prime or composite number?

23 is a prime number because it has only two distinct positive divisors: 1 and 23.

What number is divisible by 23?

Any multiple of 23 is divisible by 23. For example, 46, 69, and 92 are all divisible by 23.

What is the sum of all the factors of 23?

The sum of all the factors of 23 is 1 + 23 = 24.