Factors of 30

The factors of a number is fundamental in mathematics, as it helps in simplifying calculations and solving various mathematical problems. Factors are the integers that can be multiplied together to produce the original number. For instance, the factors of 30 are the numbers that can divide 30 without leaving a remainder. Knowing these factors is particularly useful in areas such as prime factorization, least common multiple (LCM), and greatest common divisor (GCD). Identifying the factors of 30 can also aid in various real-life applications, such as dividing objects into equal groups or solving problems related to ratios and proportions. In this article, we will explore all the factors of 30 and their significance.

What are the Factors of 30?

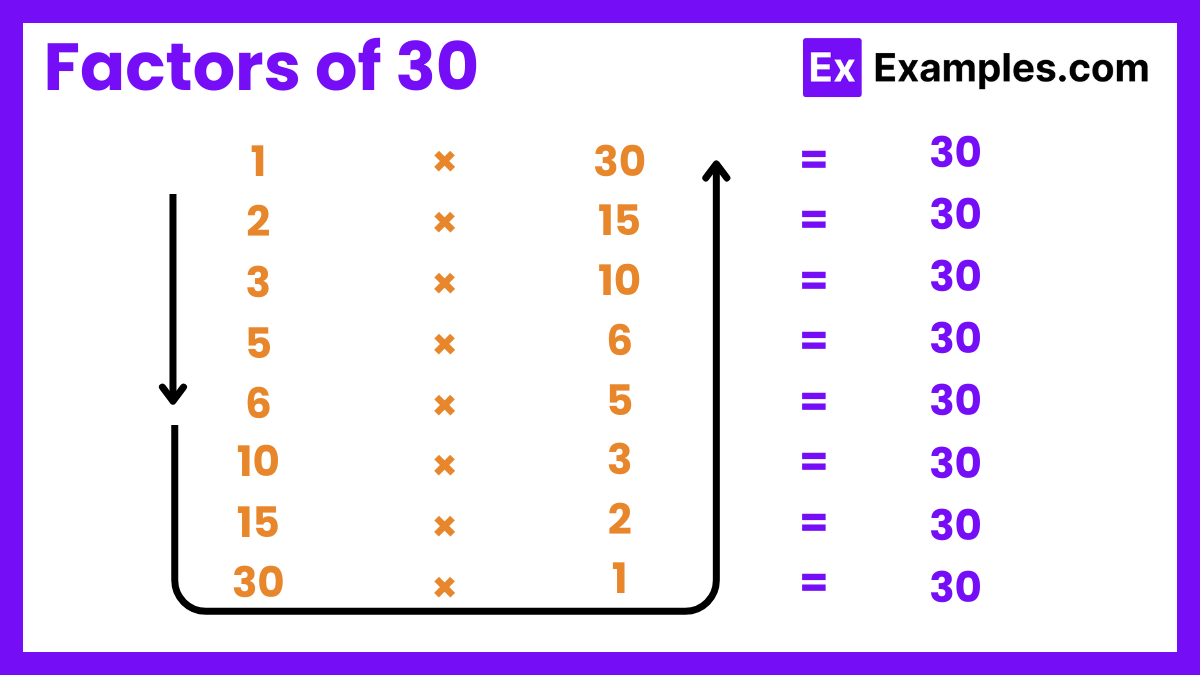
The factors of 30 are the numbers that can divide 30 without leaving a remainder. These factors include 1, 2, 3, 5, 6, 10, 15, and 30. Each of these numbers can evenly divide 30, making them its factors. Understanding the factors of 30 is useful in various mathematical applications such as simplifying fractions, finding least common multiples, and determining greatest common divisors.

Factors Pairs of 30

actor pairs of 30 are sets of two numbers that, when multiplied together, equal 30. Here are the factor pairs:

• 1 and 30: 1×30=30
• 2 and 15: 2×15=30
• 3 and 10: 3×10=30
• 5 and 6: 5×6=30

These pairs represent all the combinations of factors that result in the product of 30.

How to Calculate Prime Factors of 30

Prime factorization is the process of breaking down a composite number into its prime number factors. For 30, this involves identifying the prime numbers that multiply together to give 30. Here’s a step-by-step guide to calculating the prime factors of 30:

Step 1: Start with the Smallest Prime Number

Begin with the smallest prime number, which is 2. Check if 30 is divisible by 2.

Step 2: Divide by 2

Since 30 is an even number, it is divisible by 2. Divide 30 by 2 to get 15. So, 30÷2=15.

Step 3: Move to the Next Prime Number

Next, consider the smallest prime number greater than 2, which is 3. Check if 15 is divisible by 3.

Step 4: Divide by 3

Since 15 is divisible by 3, divide 15 by 3 to get 5. So, 15÷3=5.

Step 5: Consider the Remaining Number

The remaining number is 5, which is a prime number. This means we have reached the end of the factorization process.

The prime factors of 30 are 2, 3, and 5. Thus, the prime factorization of 30 can be written as 2×3×5.

Factors of 30: Examples

Example 1: Finding Factors of 30

Problem: Determine all the factors of 30.

Solution: Factors are numbers that divide evenly into another number. For 30:

• 1 × 30 = 30
• 2 × 15 = 30
• 3 × 10 = 30
• 5 × 6 = 30

Factors of 30: 1, 2, 3, 5, 6, 10, 15, 30

Example 2: Common Factors of 30 and 45

Problem: Find the common factors of 30 and 45.

Solution:

• Factors of 30: 1, 2, 3, 5, 6, 10, 15, 30
• Factors of 45: 1, 3, 5, 9, 15, 45

Common Factors: 1, 3, 5, 15

Example 3: Prime Factorization of 30

Problem: Express 30 as a product of its prime factors.

Solution: Prime factorization involves breaking down a number into its prime numbers:

• 30 ÷ 2 = 15
• 15 ÷ 3 = 5
• 5 ÷ 5 = 1

Prime Factorization: 30 = 2 × 3 × 5

Example 4: Greatest Common Factor (GCF) of 30 and 50

Problem: Calculate the GCF of 30 and 50.

Solution:

• Factors of 30: 1, 2, 3, 5, 6, 10, 15, 30
• Factors of 50: 1, 2, 5, 10, 25, 50

GCF: The highest common factor is 10.

Example 5: Least Common Multiple (LCM) of 30 and 20

Problem: Determine the LCM of 30 and 20.

Solution: LCM is the smallest number that is a multiple of both numbers:

• Prime factors of 30: 2 × 3 × 5
• Prime factors of 20: 2² × 5

LCM: 2² × 3 × 5 = 60

Factors of 30: Tips

Understanding the factors of 30 can be helpful in various mathematical applications, including solving problems and understanding number properties. Here are some key tips to identify and work with the factors of 30:

1. Definition of Factors: Factors are numbers that divide another number completely without leaving a remainder. For 30, any number that divides 30 exactly is a factor.
2. List of Factors: The factors of 30 are 1, 2, 3, 5, 6, 10, 15, and 30. These numbers can be paired, as each pair multiplied together gives the product of 30 (e.g., 1 x 30, 2 x 15, 3 x 10, and 5 x 6).
3. Prime Factorization: Breaking down 30 into its prime factors can simplify finding all factors. The prime factors of 30 are 2, 3, and 5 (since 30 = 2 x 3 x 5).
4. Using Prime Factors: To find all factors, combine the prime factors in different ways. For instance, multiplying 2 and 3 gives 6, a factor of 30, and so on with other combinations.
5. Divisibility Rules: Knowing basic divisibility rules helps in quickly identifying factors. For example, since 30 is even, it’s divisible by 2. It ends in 0, so it’s also divisible by 5 and 10.
6. Factor Pairs: Consider factor pairs to ensure all factors are listed. If you find 1 x 30, then also check 2 x 15, 3 x 10, and 5 x 6. Each pair should multiply to give 30.
7. Smallest and Largest Factors: The smallest factor of any number is 1, and the number itself is always the largest factor (for 30, it’s 1 and 30).
8. Factor Checking: To confirm all factors, divide 30 by each of its factors to ensure no remainders. This step ensures accuracy.
9. Applications in Problem Solving: Factors of 30 can be used in fraction simplification, finding common denominators, and solving various algebraic problems.
10. Visualization: Use a factor tree or a division table to visualize the factors. This method aids in understanding the relationship between the factors and the original number.
11. Practice: Regular practice with different numbers can enhance your ability to quickly identify factors and understand their applications.

What is the prime factorization of 30?

The prime factorization of 30 is 2 x 3 x 5. These are the prime numbers that multiply together to give 30.

Why is it important to know the factors of 30?

Knowing the factors of 30 is important for simplifying fractions, solving equations, finding greatest common divisors (GCD), and least common multiples (LCM). It’s also useful in various real-life applications like splitting objects into equal parts.

Is 30 a composite number?

Yes, 30 is a composite number because it has more than two factors. It can be divided by 1, 2, 3, 5, 6, 10, 15, and 30.

What is the sum of all the factors of 30?

The sum of all the factors of 30 (1, 2, 3, 5, 6, 10, 15, and 30) is 72.

How do you find common factors of 30 and another number?

To find common factors of 30 and another number, list the factors of both numbers and identify the common ones. For example, the factors of 20 are 1, 2, 4, 5, 10, and 20. The common factors of 30 and 20 are 1, 2, 5, and 10.

What is the greatest common factor (GCF) of 30 and 45?

The factors of 30 are 1, 2, 3, 5, 6, 10, 15, and 30. The factors of 45 are 1, 3, 5, 9, 15, and 45. The greatest common factor (GCF) of 30 and 45 is 15.

Are all factors of 30 also factors of its multiples?

Yes, all factors of 30 are also factors of any multiple of 30. For example, since 60 is a multiple of 30, the factors of 30 (1, 2, 3, 5, etc.) are also factors of 60.