Factors of 4

The number 4 has several factors that are essential to understanding its properties. The factors of 4 are 1, 2, and 4. Its prime factorization is 2 × 2 or 2². The positive pair factors of 4 are (1, 4) and (2, 2), while the negative pair factors are (-1, -4) and (-2, -2). The sum of all positive factors of 4 is 1 + 2 + 4 = 7. Knowing these factors helps in various mathematical calculations and problem-solving scenarios. This information is crucial for students and enthusiasts looking to deepen their understanding of basic number theory.

What are the Factors of 4?

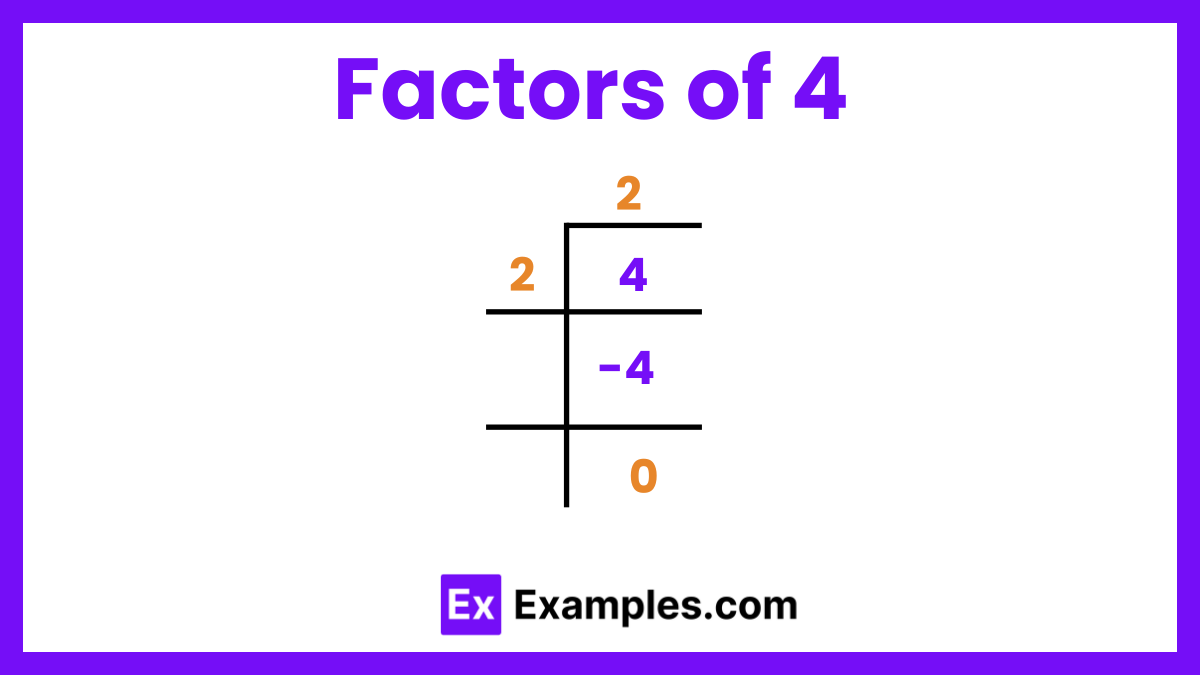
The factors of 4 are 1, 2, and 4, which means these are the numbers that can divide 4 without leaving a remainder. The prime factorization of 4 is 2×2 or 2², indicating that 4 is composed of the prime number 2 multiplied by itself. The positive pair factors of 4 are (1, 4) and (2, 2), while the negative pair factors are (-1, -4) and (-2, -2). Adding the positive factors together gives a sum of 7 (1 + 2 + 4). Understanding these factors is essential for various mathematical applications, including problem-solving and number theory.

Factors Pairs of 4

The factor pairs of 4 are combinations of two numbers that, when multiplied together, equal 4. These pairs include both positive and negative numbers.

The positive factor pairs of 4 are:

• (1, 4)
• (2, 2)

The negative factor pairs of 4 are:

• (-1, -4)
• (-2, -2)

These pairs show all the possible combinations of numbers that can be multiplied to result in 4.

How to Calculate Prime Factors of 4?

Calculating the prime factors of a number involves finding all the prime numbers that multiply together to result in the original number. Here’s how you can calculate the prime factors of 4:

Step 1: Understand What a Prime Factor

A prime factor is a prime number that can divide a given number without leaving a remainder. A prime number is a number greater than 1 that has no divisors other than 1 and itself.

Step 2: Start Dividing the Number by the Smallest Prime Number

The smallest prime number is 2. Divide 4 by 2: 4÷2=2 Since 2 is a prime number and divides 4 without leaving a remainder, 2 is a prime factor of 4.

Step 3: Repeat the Division

Now take the quotient from Step 2 and divide it again by 2: 2÷2=1 Once again, 2 divides without leaving a remainder, so 2 is again a prime factor.

Step 4: Conclusion

The process ends when the quotient is 1. The prime factors of 4 are all the prime numbers you used in the division steps, which in this case is 2, repeated twice. Thus, the prime factors of 4 are 2×2 or 2².

Factors of 4 : Examples

Example 1: Dividing by 1

• Calculation: 4÷1
• Result: 4
• Conclusion: Since 4 divided by 1 results in an integer, 1 is a factor of 4.

Example 2: Dividing by 2

• Calculation: 4÷2
• Result: 2
• Conclusion: Since 4 divided by 2 results in an integer, 2 is a factor of 4.

Example 3: Attempting to Divide by 3

• Calculation: 4÷3
• Result: Approximately 1.33 (not an integer)
• Conclusion: Since 4 divided by 3 does not result in an integer, 3 is not a factor of 4.

Example 4: Dividing by Itself

• Calculation: 4÷4
• Result: 1
• Conclusion: Since 4 divided by itself results in an integer, 4 is a factor of 4.

Example 5: Verifying a Non-Factor

• Calculation: 4÷5
• Result: 0.8 (not an integer)
• Conclusion: Since 4 divided by 5 does not result in an integer, 5 is not a factor of 4.

Factors of 4 : Tips

Here are some tips and tricks that can help you quickly find factors of numbers, especially when dealing with larger numbers or teaching this concept:

1. Start with the Smallest: Always start with the smallest factor, which is 1, and its corresponding pair that gives the target number when multiplied. In this case, 1 × 4.
2. Check for Square Roots: If the number is a perfect square (like 4, 9, 16), the square root (e.g., 2 for 4) will be a factor.
3. Increment Wisely: After 1, check the smallest numbers that are generally known to be factors of many numbers (like 2 for even numbers, 3 for numbers whose digits sum to a multiple of 3, etc.).
4. Divisibility Rules: Use divisibility rules to check if a number can be divided without a remainder by another number. For 4, if a number is even and the number formed by the last two digits is divisible by 4, then the whole number is divisible by 4.
5. Stop at Half: You only need to check factors up to half of the target number (plus one), because no number greater than half of a number (other than the number itself) can be a factor of it.
6. Use Technology: For larger numbers, consider using calculators or factorization software to help find factors quickly.
7. Practice with Examples: Regular practice with different numbers can help solidify the understanding of factorization and the quick identification of factors.

Why is 2 considered a factor of 4 twice?

2 is considered a factor of 4 twice because it can multiply by itself to yield 4 (2 × 2 = 4). In factorization, each occurrence of a factor in such a pairing is counted, so 2 is both a factor and its own pair.

Can 0 be a factor of 4?

No, 0 cannot be a factor of any number because multiplying 0 by any number always results in 0, which would not give the original number unless the original number is also 0.

Is 4 a prime number?

No, 4 is not a prime number because it has more than two factors (1, 2, and 4). A prime number has exactly two distinct factors: 1 and itself.

What are common multiples of 4?

Common multiples of 4 include 8, 12, 16, 20, and so on. These are numbers that can be evenly divided by 4.

Are there any negative factors of 4?

Yes, negative numbers can also be factors. The negative factors of 4 are -1, -2, and -4, because multiplying any pair of these negative factors results in 4 (e.g., -1 x -4 = 4).

What is the sum of the factors of 4?

The sum of the factors of 4 is 1 + 2 + 4, which equals 7. Factors are the numbers that divide the original number exactly without leaving a remainder. In this case, adding the factors 1, 2, and 4 results in a total of 7.

Is 2 a factor of 4?

Yes, 2 is a factor of 4. This is because when you divide 4 by 2, the result is 2, which is a whole number. Factors are numbers that divide another number evenly, and 2 divides 4 without leaving any remainder.