Trigonometry

Last Updated: August 23, 2024

Notes

Trigonometry for ACT Exam is a branch of mathematics that studies the relationships between the sides and angles of triangles. It is essential for solving problems involving right triangles and circles, and it has applications in various fields such as physics, engineering, and architecture. On the ACT Math section, you can expect questions that test your understanding of trigonometric functions, identities, and equations.

Learning Objectives

In the topic of Trigonometry for the ACT Math exam, you should focus on understanding and applying the basic trigonometric functions: sine, cosine, and tangent. Learn how to use the unit circle, evaluate trigonometric functions for common angles, and solve right triangles using SOHCAHTOA. Study the relationships and identities, such as the Pythagorean identity, and practice solving trigonometric equations. Additionally, familiarize yourself with graphing trigonometric functions and applying trigonometry in real-world contexts.

Basic Trigonometric Functions

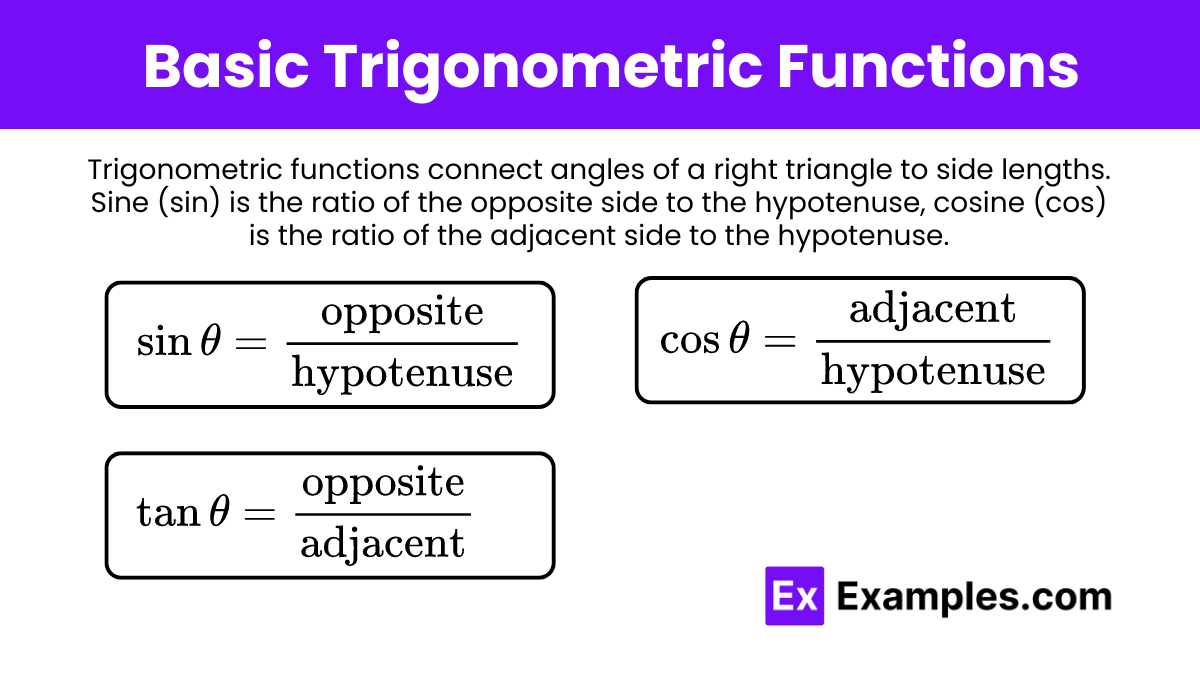
Trigonometric functions connect angles of a right triangle to side lengths. Sine (sin) is the ratio of the opposite side to the hypotenuse, cosine (cos) is the ratio of the adjacent side to the hypotenuse, and tangent (tan) is the ratio of the opposite side to the adjacent side.

Sine (sin)

$\sin \theta = \frac{\text{opposite}}{\text{hypotenuse}}$
In a right triangle, the sine of an angle is the ratio of the length of the side opposite the angle to the length of the hypotenuse.

Cosine (cos)

$\cos\theta = \frac{\text{adjacent}}{\text{hypotenuse}}$
The cosine of an angle is the ratio of the length of the adjacent side to the hypotenuse.

Tangent (tan)

$\tan\theta = \frac{\text{opposite}}{\text{adjacent}}$
The tangent of an angle is the ratio of the length of the opposite side to the adjacent side.

Reciprocal Trigonometric Functions

Reciprocal trigonometric functions are derived from the primary trigonometric functions: sine, cosine, and tangent. They are essential in advanced mathematics, especially in calculus and trigonometry. Understanding these functions helps solve complex problems involving angles and right triangles.

Cosecant (csc)
- $\csc \theta = \frac{1}{\sin \theta} = \frac{\text{hypotenuse}}{\text{opposite}}$
Secant (sec)
- $\sec\theta = \frac{1}{\cos\theta} = \frac{\text{hypotenuse}}{\text{adjacent}}$
Cotangent (cot)
- $\cot\theta = \frac{1}{\tan\theta} = \frac{\text{adjacent}}{\text{opposite}}$

Key Trigonometric Identities

Trigonometric identities are equations involving trigonometric functions that hold true for all angles. These identities are crucial for simplifying expressions, solving trigonometric equations, and proving other mathematical properties. Here are some of the most important trigonometric identities:

Pythagorean Identities

sin⁡²θ+cos⁡²θ=1
1+tan⁡²θ=sec⁡²θ
1+cot⁡²θ=csc⁡²θ

Angle Sum and Difference Identities

sin⁡(a±b)=sin⁡acos⁡b±cos⁡asin⁡b
cos⁡(a±b)=cos⁡acos⁡b∓sin⁡asin⁡b
$\tan(a \pm b) = \frac{\tan a \pm \tan b}{1 \mp \tan a \tan b}$

Double Angle Identities

sin⁡2θ=2sin⁡θcos⁡θ
cos⁡2θ=cos⁡²θ−sin⁡²θ
$\tan 2\theta = \frac{2 \tan \theta}{1 - \tan^2 \theta}$

Half Angle Identities

$\sin \frac{\theta}{2} = \pm \sqrt{\frac{1 - \cos \theta}{2}}$

$\cos \frac{\theta}{2} = \pm \sqrt{\frac{1 + \cos \theta}{2}}$

$\tan \frac{\theta}{2} = \pm \sqrt{\frac{1 - \cos \theta}{1 + \cos \theta}} = \frac{\sin \theta}{1 + \cos \theta} = \frac{1 - \cos \theta}{\sin \theta}$

Solving Trigonometric Equations

Solving trigonometric equations is a fundamental aspect of trigonometry, essential for understanding various real-world applications in physics, engineering, and other fields. Trigonometric equations involve functions such as sine, cosine, tangent, and their inverses. These equations can range from simple to complex, often requiring algebraic manipulation and the use of trigonometric identities to find solutions.

Basic Equations
- Solve for θ in equations like
  $\sin \theta = \frac{1}{2}$
  or tan⁡θ=1.
- Use the unit circle and inverse trigonometric functions to find solutions.
Using Identities
- Apply trigonometric identities to simplify and solve equations.
- Example: Solve cos⁡2θ=cos⁡θ.

Applications of Trigonometry

Right Triangle Problems
- Use trigonometric functions to find missing sides or angles in right triangles.
Circular Functions
- Understand the relationship between trigonometric functions and the unit circle.
- Determine the coordinates of a point on the unit circle given an angle θ\thetaθ.
Graphs of Trigonometric Functions
- Know the shape, period, amplitude, and phase shift of sine, cosine, and tangent functions.

Tips for ACT Trigonometry

Memorize Key Identities
- Knowing the basic identities and how to apply them is crucial for solving trigonometry problems quickly.
Practice with Right Triangles
- Be comfortable with using SOHCAHTOA and the Pythagorean Theorem in various problems.
Use the Unit Circle
- Familiarize yourself with the unit circle, including the values of sine and cosine at key angles (0°, 30°, 45°, 60°, 90°, etc.).

Solve Practice Problems

Work through ACT practice tests and trigonometry-specific problems to build confidence and speed.

Examples

Example 1: Finding the Sine of an Angle

Problem: Calculate the sine of a 30° angle.

Solution: The sine of an angle in a right triangle is defined as the ratio of the length of the opposite side to the length of the hypotenuse. For a 30° angle in a right triangle, this ratio is known to be 1/2.

$\sin(30°) = \frac{1}{2}$

Thus, the sine of a 30° angle is 0.5.

Example 2: Using the Pythagorean Identity

Problem: Verify the Pythagorean identity for a 45° angle: sin2(θ)+cos2(θ)=1.

Solution:
For a 45° angle, the sine and cosine values are:

$\sin(45°) = \frac{\sqrt{2}}{2}$

$\cos(45°) = \frac{\sqrt{2}}{2}$

Substituting these values into the Pythagorean identity:

$\left(\frac{\sqrt{2}}{2}\right)^2 + \left(\frac{\sqrt{2}}{2}\right)^2 = \frac{2}{4} + \frac{2}{4} = 1$

This verifies the identity \sin^2(\theta) + \cos^2(\theta) = 1 for \theta = 45°.

This verifies the identity sin2(θ)+cos2(θ)=1 for θ=45°.

Example 3: Calculating Tangent Using Sine and Cosine

Problem: Find the tangent of a 60° angle using its sine and cosine values.

Solution: The tangent of an angle is the ratio of the sine to the cosine of that angle. For a 60° angle, we have:

$\sin(60°) = \frac{\sqrt{3}}{2}$

$\cos(60°) = \frac{1}{2}$

Using the tangent definition:

$\tan(60°) = \frac{\sin(60°)}{\cos(60°)} = \frac{\frac{\sqrt{3}}{2}}{\frac{1}{2}} = \sqrt{3}$

So, the tangent of a 60° angle is $\sqrt{3}$.

Example 4: Solving for an Angle Using Inverse Trigonometric Functions

Problem: Determine the angle θ if sin(θ)=0.866.

Solution: To find the angle whose sine is 0.866, we use the inverse sine function (arcsin):

θ=arcsin(0.866)

Using a calculator or reference table:

θ≈60°

Therefore, the angle θ is approximately 60 degrees.

Example 5: Applying the Law of Sines

Problem: In triangle ABC, where a=7, b=9, and ∠A=30°, find ∠B.

Solution: The Law of Sines states:

$\frac{a}{\sin(A)} = \frac{b}{\sin(B)}$

Substitute the known values:

$\frac{7}{\sin(30°)} = \frac{9}{\sin(B)}$

Since sin⁡(30°)=0.5:

$\frac{7}{0.5} = \frac{9}{\sin(B)}$

$14 = \frac{9}{\sin(B)}$

$\sin(B) = \frac{9}{14} \approx 0.643$

Using the inverse sine function:

B=arcsin(0.643)≈40°

Thus, ∠B is approximately 40 degrees.

Multiple Choice Questions

Question 1

What is the value of sin⁡30⁰?

$\text{A) } \frac{\sqrt{3}}{2}$

$\text{B) } \frac{1}{2}$

$\text{C) } \frac{1}{\sqrt{2}}$

$\text{D) } \sqrt{3}$

$\text{Answer: B) } \frac{1}{2}$

Explanation: The sine of an angle in a right triangle is defined as the ratio of the length of the opposite side to the hypotenuse. For a 30-degree angle in a right triangle (half of an equilateral triangle), the opposite side is half the hypotenuse. Therefore, sin30⁰=

$\frac{1}{2}$