Real Numbers – 7+ Examples, How to Discern

Delve into the essential world of real numbers, a key component of mathematics that spans from the simplest natural numbers to the complexities of irrational numbers. This guide is specifically crafted for educators looking to refine their teaching approach, making mathematical concepts more relatable and understandable for students. It breaks down sophisticated ideas into straightforward, easy-to-grasp explanations, utilizing plain English to facilitate better comprehension. Aimed at enhancing classroom discussions and student engagement, this resource supports teachers in demystifying the realm of real numbers, fostering an environment where students can confidently navigate through the intricacies of mathematics.

What Is a Real Number

A real number is defined as a set of numbers along all the possible points in a continuous and infinite straight line. Real numbers have plenty of real-life applications and are essential for some of our everyday tasks.

What is the Best Example of Real Numbers?

The square root of 2 (?2) serves as a compelling example of real numbers, particularly illustrating the concept of irrational numbers, which are a subset of real numbers. This number, approximately equal to 1.41421, cannot be expressed as a fraction of two integers, distinguishing it from rational numbers. Its discovery is attributed to the ancient Greeks who realized that the diagonal of a square with unit sides could not be measured exactly by any ratio of whole numbers, thus challenging the completeness of rational numbers.

Properties of Real Numbers

Understanding the properties of real numbers is essential for both teaching and learning mathematics, as these properties form the foundation for algebra and beyond. Real numbers include all the numbers on the number line, encompassing both rational and irrational numbers. Grasping these properties can significantly enhance students’ problem-solving skills and mathematical reasoning. Let’s explore these properties in detail, providing teachers with clear examples to facilitate effective teaching.

1. Associative Property

The associative property states that the way numbers are grouped in an operation (addition or multiplication) does not change the result.

Examples:

1. (3 + 4) + 5 = 3 + (4 + 5)Both groupings equal 12, demonstrating the associative property of addition.
2. (2 × 3) × 4 = 2 × (3 × 4)Both sides yield 24, illustrating the associative property of multiplication.

2. Commutative Property

The commutative property highlights that the order in which two numbers are added or multiplied does not affect the outcome.

Examples:

1. 7 + 5 = 5 + 7Swapping the order of addition does not change the sum, 12.
2. 6 × 9 = 9 × 6Changing the order of the factors does not alter the product, 54.

3. Distributive Property

The distributive property connects multiplication with addition or subtraction, distributing the former over the latter.

Examples:

1. 3 × (4 + 5) = (3 × 4) + (3 × 5)This property shows how multiplication is distributed over addition, resulting in 27 on both sides.

4. Identity Property

The identity property of addition and multiplication shows that adding 0 or multiplying by 1 leaves a number unchanged.

Examples:

1. 8 + 0 = 8Adding zero does not change the value, illustrating the identity property of addition.
2. 7 × 1 = 7Multiplying by one keeps the number the same, showing the identity property of multiplication.

5. Inverse Properties

The inverse properties refer to adding a number and its opposite or multiplying a number by its reciprocal to get the identity element (0 or 1).

Examples:

1. 9 + (-9) = 0Adding a number and its additive inverse yields zero.
2. 5 × (1/5) = 1Multiplying a number by its reciprocal results in one.

6. Closure Property

The closure property states that the sum or product of any two real numbers is also a real number.

Examples:

1. 3 + 2 = 5The sum of two real numbers is a real number.
2. 4 × 5 = 20The product of two real numbers is a real number.

7. Multiplicative Identity

The multiplicative identity property confirms that any number multiplied by 1 remains unchanged.

Examples:

1. 10 × 1 = 10Multiplying by 1 does not alter the original number.

8. Properties of Zero

The properties of zero include its role in addition, where adding zero to a number leaves it unchanged, and in multiplication, where any number multiplied by zero equals zero.

Examples:

1. 12 + 0 = 12Zero added to any number does not change the number.
2. 15 × 0 = 0Any number multiplied by zero equals zero.

Set of Real Numbers

The set of real numbers encompasses all the numbers that can be found on the number line, including both rational numbers (such as integers and fractions) and irrational numbers (such as the square root of non-perfect squares and ?). Understanding the set of real numbers is crucial for students as it lays the groundwork for all higher mathematics.

Examples:

1. 5 (an integer)A clear example of a rational number, perfectly placed on the number line.
2. 2/3 (a fraction)Represents a rational number, indicating a precise value on the number line.
3. ?2An irrational number, it cannot be precisely expressed as a fraction, showcasing the diversity within the set of real numbers.
4. ? (pi)An irrational number known for its endless, non-repeating decimal representation, highlighting the complexity within the set of real numbers.
5. -8.75A negative rational number, demonstrating that real numbers include both positive and negative values, as well as zero.

These properties and examples of real numbers serve as foundational concepts in mathematics, facilitating students’ understanding of more complex topics. Teachers can use these clear, distinct examples to illustrate each property, aiding students in grasping these fundamental mathematical principles.

Real Numbers Chart

Real numbers include all the numbers on the number line, encompassing both rational and irrational numbers, making them a fundamental concept in mathematics. This chart helps students visualize the complete set of numbers that they can encounter in both theoretical and practical mathematical problems.

Examples for Real Numbers Chart

1. Rational Numbers (1/2?, 3/4, 5): These numbers can be expressed as fractions or whole numbers. For instance, 1221? represents a simple division that results in a finite decimal or a repeating decimal, making it easy to plot on a real numbers chart.
2. Irrational Numbers (?2?, $?$, $e$): Numbers like ?2? cannot be expressed as a simple fraction, and its decimal form is non-repeating and infinite. It exemplifies the complexity and beauty of the real numbers system.
3. Integers (-1, 0, 2): These include negative numbers, zero, and positive numbers without any fractional or decimal part. They are crucial for understanding the full spectrum of real numbers.
4. Whole Numbers (0, 1, 2): Starting from zero and moving upwards, whole numbers form the basis of counting and are integral to the real number system.
5. Natural Numbers (1, 2, 3): Excluding zero, natural numbers are the simplest form of numbers used for counting and ordering, essential for basic mathematics.

Real Numbers on a Number Line

A number line is a visual representation that shows the order of real numbers. It is an effective tool for teaching students about the concept of positive and negative numbers, as well as the infinite nature of real numbers.

Examples for Real Numbers on a Number Line

1. Zero (0): The central point on a number line, dividing positive and negative numbers. It is fundamental in understanding the balance and symmetry in mathematics.
2. Positive Rational Numbers (2, 3.5): Numbers like 2 or 3.5 lie to the right of zero on the number line, demonstrating the concept of magnitude and distance from zero.
3. Negative Rational Numbers (-1, -2.5): Positioned to the left of zero, these numbers illustrate the idea of negative magnitude and are essential for understanding operations like subtraction.
4. Irrational Numbers ($?$, ?3?): These numbers show that not all points on the number line can be exactly represented by fractions, introducing students to the depth of real numbers.
5. Positive and Negative Integers (-3, 4): They help students grasp the idea of whole numbers existing on both sides of zero, emphasizing the concept of opposites in mathematics.

These examples serve as tools for teachers to explain the vast and inclusive world of real numbers to students. By utilizing charts and number lines, educators can demystify complex concepts, making mathematics more accessible and engaging for learners.

Understanding Real Numbers

Real numbers encompass all the numbers on the number line, including rational numbers (fractions, terminating, and repeating decimals) and irrational numbers (non-repeating, non-terminating decimals). This vast category represents quantities that can be found in everyday life, from measurements to financial transactions, making it a foundational concept in mathematics.

Difference Between Real Numbers and Integers

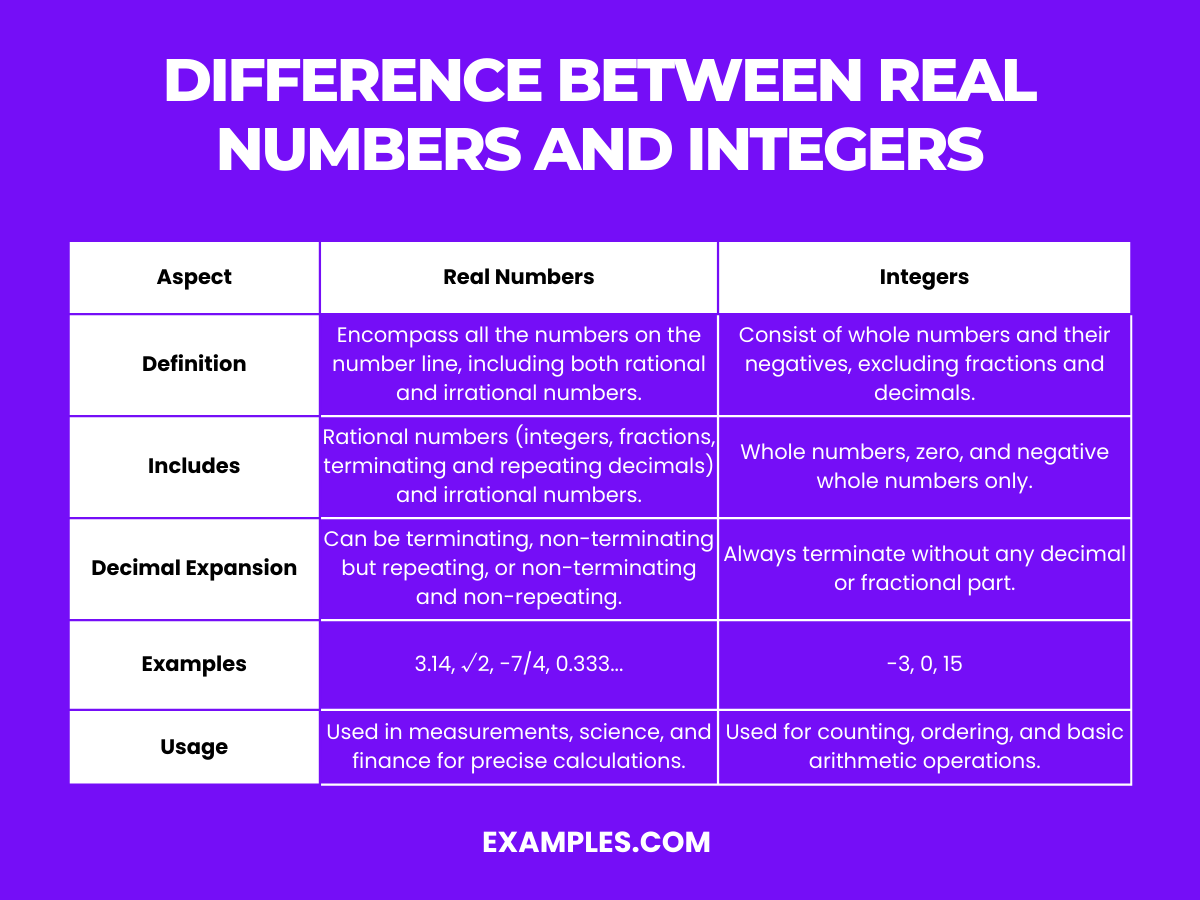
To clarify the distinctions between real numbers and integers, let’s examine their characteristics side by side in a table format:

This table serves as a quick reference for teachers aiming to explain the nuanced differences between real numbers and integers to students, enhancing their understanding of mathematical concepts.

Decimal Expansion of Real Numbers

Decimal expansion in real numbers refers to the way these numbers are expressed in decimal form. This expansion reveals whether a number is rational or irrational, based on the pattern and termination of its decimal digits.

Examples of Decimal Expansion in Real Numbers

1. Terminating Decimal: 0.75
   • A rational number because its decimal form ends after a finite number of digits.
   • Represents a fraction (3/4?) in decimal form.
2. Repeating Decimal: 0.3?3
   • Also a rational number, characterized by a repeating pattern in its decimal digits.
   • Equivalent to 1/3?, showcasing a simple fraction as a repeating decimal.
3. Non-Terminating, Non-Repeating Decimal: ? (Pi)
   • An irrational number known for its endless, non-repeating decimal sequence.
   • Widely used in mathematics to represent the ratio of a circle’s circumference to its diameter.
4. Square Root of 2 (?2?)
   • Another example of an irrational number, unable to be precisely represented as a fraction.
   • Its decimal form is non-terminating and non-repeating, essential in geometry.
5. Rational Number: 1.2
   • Represents a simple fraction (6/5?) in decimal form, terminating after one digit.
   • A clear example of how rational numbers can have a finite decimal representation.

These examples are tailored for teachers to help students grasp the concept of decimal expansion in real numbers, illustrating the diversity of these numbers and their applications in various mathematical contexts. Understanding these expansions aids in recognizing the nature of numbers and their classifications, enhancing students’ numerical literacy.

How to Discern which Type of Real Number a Specific Number is

Real numbers can be divided into two different types, each with its specific purpose. These two types are called rational numbers and irrational numbers. If you are still confused or unsure about the whole concept of real numbers you may view any of the real number samples, examples, templates, and PDFs on the list above.

1.) Write Down the Number

Begin by writing down the number on a physical notepad or digital note-taking software. This will allow you to visualize the set of given numbers, and ensure you will have an easy time simplifying any fractions, or equations.

2.) Express the Number in its Simplest Form

After you have written down the number you must express it in its simplest form. This is to make the process of equating a fraction or an equation easier to process.

3.) If the Number is an Equation, Solve the Equation

If the given set of numbers forms an equation, you must solve the equation before you can determine which type of real number the equation is. Note, observe proper signs for the integers.

4.) If the Number is a Fraction, Divide the Fraction

If the given number is a fraction, you must divide the fraction to check if the quotient of the fraction is an infinite number, a decimal number, or a whole number.

5.) Distinguish Which Type of Real Number

When you have finished doing all the steps above, you may now distinguish whether the given set of real numbers is either a rational or an irrational number. Just note, that all irrational numbers are infinite numbers.

FAQs

Real vs rational numbers; what is the difference between real and rational numbers?

Real numbers are numbers that describe all the points on a continuous straight line that ranges towards infinity. Rational numbers, on the other hand, are numbers or sets of numbers that can be expressed as a decimal, a whole number, or a fraction. This means not all real numbers are rational but all rational numbers are real numbers, setting real numbers as an umbrella term used in mathematics.

What are Natural and Real Numbers?

Natural numbers are positive integers from 1 upwards. Real numbers include all rational and irrational numbers, encompassing natural numbers, whole numbers, integers, and more.

Is Zero a Real or an Imaginary Number?

Zero is a real number. It represents a null quantity and is integral to the real number system, lying between positive and negative integers.

Is ?3 a Real Number?

Yes, ?3 is a real number. It is an irrational number that cannot be precisely represented as a simple fraction.

What is the importance of real numbers, and how do I use them in real life?

Real numbers allow people to represent a specific numerical point that can or has been reached. This means that people can use real numbers to numerically set objectives for themselves, like a weight goal or a timed event. Not only that but real numbers can also be used to represent time, the number of ingredients, and more the like.

Real numbers are sets of numbers that are set alongside a straight line that edges towards infinity. This means that real numbers are the numbers we use to denote numerical values in our everyday lives.