What is \( 4.2 \times 10^3 \) in standard notation?
420
4,200
42,000
420,000

When we work with big, immeasurable digits, whether rational or irrational numbers, understanding the mathematical problem becomes too hard the solution can come up as impossible. Because of the brilliant brains who created it, working with very large or tiny numbers is much less of a challenge in the scientific and engineering fields using Scientific Notation.
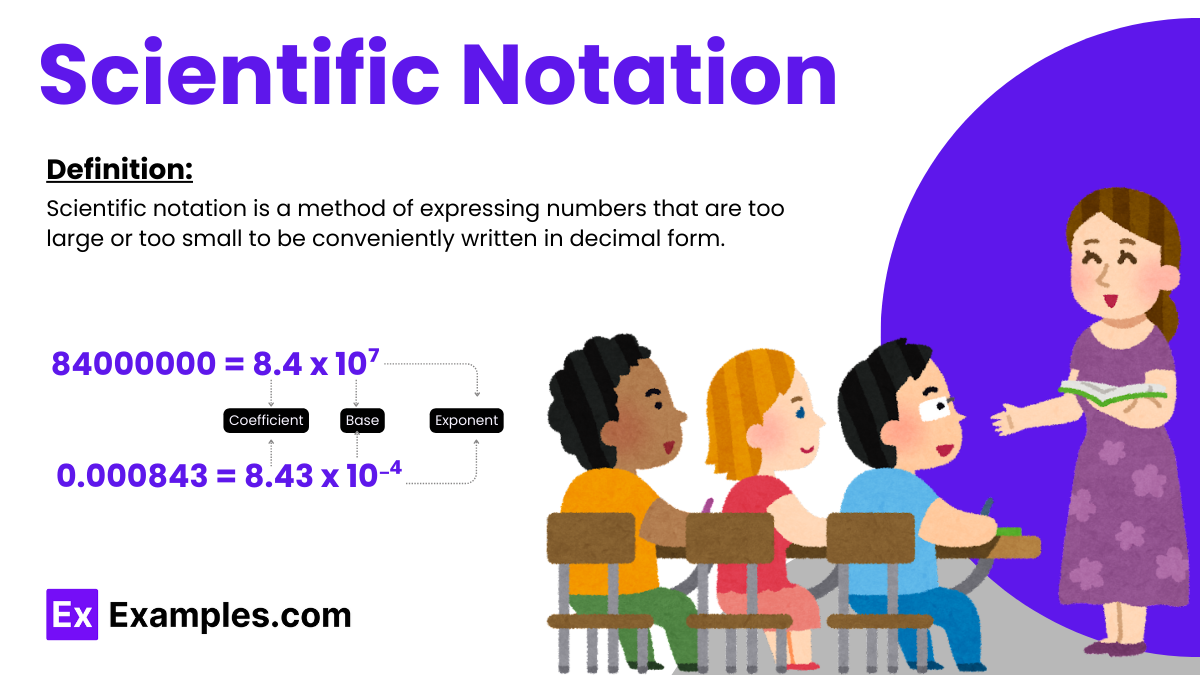
Scientific notation is a method of expressing numbers that are too large or too small to be conveniently written in decimal form. It is often used in science, engineering, and mathematics to make calculations with very large or very small numbers more manageable

The general representation of scientific notation is:
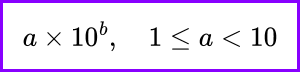
The examples of scientific notation are:
590000000 = 5.9×108
7230000000 = 7.23×109
90500000 = 9.05 x 107
0.000000047 = 4.7 x 10-8
0.0000315 = 3.15 x 10-5
Scientific notation with positive and negative exponents is a versatile way to express a wide range of numbers, from very large to very small. Here’s how these exponents function within the context of scientific notation:
In scientific notation, a positive exponent indicates a number greater than 1. The exponent tells us how many times to multiply the number by ten. For example:
These are typically used to represent large numbers such as distances in astronomy, large amounts of data in bytes, or other significant quantities.
Conversely, a negative exponent signifies a number less than 1. This exponent denotes how many times the number is divided by ten. For instance:
Negative exponents are common when dealing with microscopic scales, such as the sizes of
When positive real numbers are multiplied by a power of 10, the result is expressed in scientific notation. Here’s how to do it step by step.
When calculating numbers through multiplication or division using scientific notation, we must keep in mind the rules for standard forms of exponents since they are a component of the number (10 raised to a power). Consider this: “How many places can I move the decimal point?” to determine the power of 10.
To get a number between 1 and 10 (including fractions), move the decimal point. In other words, you should place your decimal after the first non-zero integer.
The count is positive if the decimal point was shifted to the left. The count becomes negative if the decimal point is shifted to the right.
After changing the number to Scientific Notation, just make sure the “digits” component is between 1 and 10. It may be 1, but never 10.
6.3 is already in a form suitable for scientific notation as 6.3×10⁰ , where the exponent indicates that the decimal point has not moved..
In contexts involving e (Euler’s number), scientific notation uses “e” to denote powers of ten, as in 1.2e3 for 1.2 x 10³
To convert from scientific to standard notation, shift the decimal point in the coefficient right for positive exponents or left for negative exponents by the value of the exponent.
For 7th graders, scientific notation is a way to write very large or small numbers using a coefficient between 1 and 10 multiplied by a power of ten.
The number 10,000,000,000 is written in scientific notation as 1×10¹⁰
In mathematics, e typically represents Euler’s number, approximately 2.718, which is the base of natural logarithms, used in continuous growth or decay processes.
The three steps are: 1) Move the decimal point in the number to create a new number from 1 up to 10; 2) Count the number of places the decimal moved; 3) Write as a product of the new number and 10 raised to the count.
“10 raised to the power” refers to exponential notation where 10 is multiplied by itself a specified number of times, such as 10³=1000.
Yes, a negative number can be written in scientific notation by placing a minus sign before the coefficient, e.g.,−3.4×10²
Text prompt
Add Tone
10 Examples of Public speaking
20 Examples of Gas lighting
What is \( 4.2 \times 10^3 \) in standard notation?
420
4,200
42,000
420,000
How is \( 0.0075 \times 10^4 \) written in standard form?
7.5
75
750
7,500
What is the result of \( 3.6 \times 10^{-2} \) in decimal notation?
0.036
0.36
3.6
36
Convert \( 7.8 \times 10^5 \) to standard form.
78,000
780,000
7,800,000
78,000,000
Express \( 1.2 \times 10^{-4} \) in standard notation.
0.00012
0.0012
0.012
0.12
What is the standard notation of \( 3.1 \times 10^{-5} \)?
0.000031
0.00031
0.0031
0.031
Express \( 2.5 \times 10^2 \) in standard notation.
25
250
2,500
25,000
What is \( 0.0008 \times 10^6 \) in scientific notation?
\( 8 \times 10^2 \)
\( 8 \times 10^3 \)
\( 8 \times 10^4 \)
\( 8 \times 10^5 \)
How is \( 9.2 \times 10^{-4} \) written in standard form?
0.0092
0.00092
0.00092
0.000092
What is the result of \( 4.4 \times 10^{-1} \) in decimal form?
0.44
4.4
44
440
Before you leave, take our quick quiz to enhance your learning!

