Even
Even and Odd Numbers with this comprehensive guide, designed to demystify these fundamental mathematical concepts for teachers and students alike. Even and odd numbers form the basis of numerous mathematical operations and theories, making their understanding crucial from an early age. This guide offers easy-to-understand examples and explanations, aiming to enhance mathematical literacy and communication. Tailored for educational success, it provides the tools needed for teachers to convey these concepts effectively and for students to grasp and apply them confidently.
What are Even & Odd Numbers? Definition
Even numbers are integers that can be divided evenly by 2, without leaving a remainder, such as 2, 4, 6, and so on. Odd numbers, on the other hand, cannot be evenly divided by 2, resulting in a remainder, and include numbers like 1, 3, 5, etc. Understanding the distinction between even and odd numbers is essential for grasping more complex mathematical concepts, making this knowledge foundational for students of all ages.
What is the Best Example of Even & Odd Numbers?
A practical example of even and odd numbers is organizing students into groups. If you have 20 students (an even number), you can divide them into equal groups of 2, 4, 5, or 10 with no one left out. However, with 21 students (an odd number), any attempt to divide them into equal groups of 2, 4, 5, or 10 will always leave at least one student without a group, illustrating the inherent difference between even and odd numbers in a relatable and educational context
Even and Odd Numbers Flowchart
Set Representation of Even and Odd Numbers
Even and odd numbers can be distinctly categorized into sets based on their divisibility by 2. The set representation simplifies the understanding of these numbers, aiding in mathematical operations and problem-solving. It visually separates numbers into two clear groups, facilitating easier identification and manipulation, especially beneficial in teaching concepts of number theory and arithmetic progressions to students.
- Set of Even Numbers: {2, 4, 6, 8, 10, …}
- Every number in this set is divisible by 2 without a remainder, representing numbers that can be evenly split into two groups.
- Set of Odd Numbers: {1, 3, 5, 7, 9, …}
- Numbers in this set leave a remainder of 1 when divided by 2, indicating they cannot be evenly divided into two groups without a remainder.
- Pattern Recognition: Even numbers always end with 0, 2, 4, 6, or 8, while odd numbers end with 1, 3, 5, 7, or 9, aiding in quick identification.
- Sequential Order: Even and odd numbers alternate in sequence, showcasing a predictable pattern that helps in teaching counting and sequencing skills.
- Infinite Sets: Both sets are infinite, illustrating the concept of infinity in mathematics by showing that even and odd numbers continue indefinitely.
Properties of Even and Odd Numbers
Even and odd numbers exhibit unique properties that are crucial in various mathematical operations and theories. These properties are instrumental in understanding more complex concepts like divisibility rules, algebraic expressions, and patterns within number sets.
1. Addition: Adding two even numbers or two odd numbers always results in an even number. This demonstrates the stability of evenness under addition.
2. Subtraction: Subtracting two even numbers or two odd numbers produces an even number, showing consistency in numerical operations.
3. Multiplication: Multiplying an even number by any other number always yields an even number, highlighting the dominance of evenness in multiplication.
Even Plus Odd: Adding an even number to an odd number results in an odd number, showcasing the interaction between the two sets.
Odd Multiplication: Multiplying two odd numbers always gives an odd number, illustrating a unique characteristic of odd numbers in multiplication.
How to Check if a Number is an Even or Odd Number?
Determining whether a number is even or odd is a fundamental skill in mathematics, crucial for foundational understanding and application in various mathematical contexts. This process involves simple checks that can be easily taught and understood.
- Divisibility by 2: If a number can be divided by 2 without leaving a remainder, it is even. This is the most direct method of identification.
- Last Digit Check: Observing the last digit of a number. If it ends in 0, 2, 4, 6, or 8, the number is even; if it ends in 1, 3, 5, 7, or 9, it is odd.
- Subtraction Method: Subtracting 1 from an even number will result in an odd number, and vice versa. This method helps in understanding the close relationship between even and odd numbers.
- Using Modulo Operation: In programming and advanced mathematics, the modulo operation can be used to check if a number is even or odd by calculating the remainder when divided by 2.
- Pattern Recognition: Recognizing patterns in sequences of numbers also aids in identifying whether numbers are even or odd, leveraging the alternation between even and odd numbers in a number series.
Even and Odd Numbers Examples
Even and odd numbers are integral to understanding mathematical patterns and concepts. Even numbers, divisible by 2, include 0, 2, 4, etc., while odd numbers, not evenly divisible by 2, include 1, 3, 5, etc. These examples not only serve as the foundation for arithmetic operations but also play a crucial role in various mathematical theories and applications, from basic counting to complex algebra.
- Using Even Numbers in Daily Life: When you split a pizza into 4 even slices, each person gets an equal share, illustrating even distribution.
- Using Odd Numbers in Decoration: Decorators often use an odd number of elements, like 3 vases, to create visual interest and balance.
- Counting Money with Even Numbers: When saving $2 a day, you ensure an even growth of your savings, showcasing accumulation through even numbers.
- Measuring Length with Odd Numbers: When measuring lengths, if you end up with a measurement like 31 inches, you’re dealing with an odd number in real-life application.
- Organizing Seats in Rows: If a classroom has rows of 6 seats, every row can be filled completely, but with 5 seats per row, the arrangement changes if the student count isn’t divisible by 5.
What are Even and Odd Decimals?
Even and odd numbers typically apply to integers. However, the concept doesn’t directly translate to decimals since evenness and oddness depend on divisibility by 2. Decimals, representing fractions or parts of numbers, cannot be strictly classified as even or odd in the traditional sense. This highlights the complexity and specificity of mathematical classifications, underscoring the importance of context in mathematical concepts.
Why is Zero an Even Number?
Zero is considered an even number because it meets the criteria of being divisible by 2 without leaving a remainder. This classification is fundamental to the structure of number theory and arithmetic operations. Including zero as an even number allows for a consistent application of mathematical rules and simplifies various computations and algebraic methods, making it a pivotal point in understanding numerical properties and relationships.
Difference Between Even and Odd Numbers
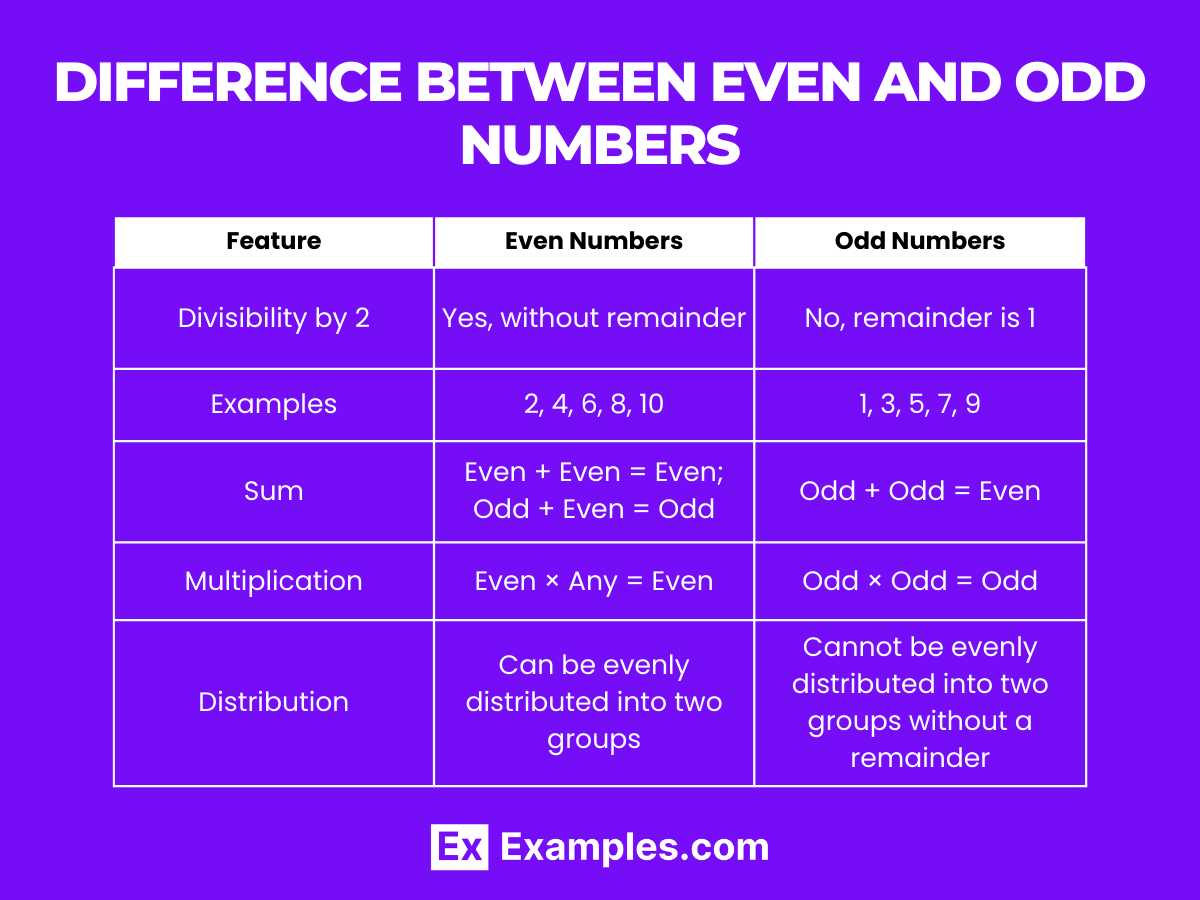
The distinction between even and odd numbers is a fundamental concept in mathematics, essential for developing numerical understanding and analytical skills. Even numbers are divisible by 2 without a remainder, indicating uniform distribution, while odd numbers, when divided by 2, leave a remainder of 1, reflecting an uneven distribution. This differentiation is crucial in various mathematical operations, including division, multiplication, and understanding patterns within the number system.
| Feature | Even Numbers | Odd Numbers |
|---|---|---|
| Divisibility by 2 | Yes, without remainder | No, remainder is 1 |
| Examples | 2, 4, 6, 8, 10 | 1, 3, 5, 7, 9 |
| Sum | Even + Even = Even; Odd + Even = Odd | Odd + Odd = Even |
| Multiplication | Even × Any = Even | Odd × Odd = Odd |
| Distribution | Can be evenly distributed into two groups | Cannot be evenly distributed into two groups without a remainder |
Odd and Even Numbers 1 to 100
Even Numbers 1 to 100 :
2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42, 44, 46, 48, 50, 52, 54, 56, 58, 60, 62, 64, 66, 68, 70, 72, 74, 76, 78, 80, 82, 84, 86, 88, 90, 92, 94, 96, 98, 100.
Odd Numbers 1 to 100 :
1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33, 35, 37, 39, 41, 43, 45, 47, 49, 51, 53, 55, 57, 59, 61, 63, 65, 67, 69, 71, 73, 75, 77, 79, 81, 83, 85, 87, 89, 91, 93, 95, 97, 99.
Identifying odd and even numbers within the range of 1 to 100 is a practical exercise for understanding their distribution and pattern recognition.
- Even Numbers Example: 2, 4, 6, 8, 10
- These are the first five even numbers. They can be divided by 2 evenly, showcasing a pattern of uniformity and balance.
- Odd Numbers Example: 1, 3, 5, 7, 9
- The initial set of odd numbers illustrates the concept of indivisibility by 2, emphasizing an irregular distribution.
- Transition from Odd to Even: 49, 50
- Transition points, like moving from 49 (odd) to 50 (even), highlight the alternating pattern of odd and even numbers.
- Midpoint Even Number: 50
- As a midpoint in the 1 to 100 range, 50 exemplifies the characteristic of even numbers to be halved into two equal parts.
- High-End Odd Number: 99
- Near the upper limit, 99 stands out as an odd number, demonstrating the perpetual alternation between odd and even numbers in any sequence.
Tips on Even and Odd Numbers
Understanding even and odd numbers is pivotal for mathematical fluency. Here are some tips to recognize and utilize these numbers effectively:
- Visual Patterns
- Use visual aids or blocks to group numbers, enhancing comprehension of even and odd distributions.
- Practical Application
- Apply the concept to real-life scenarios, such as dividing objects or people, to illustrate the practical implications of even and odd numbers.
- Use of Number Lines
- Employ number lines to visually demonstrate the alternating pattern of even and odd numbers, fostering a better grasp of numerical sequences.
- Interactive Games
- Incorporate games and puzzles that involve sorting or identifying even and odd numbers, making learning engaging and interactive.
- Mathematical Operations
- Practice adding, subtracting, and multiplying even and odd numbers to understand the resulting patterns and reinforce their properties through repetition and application.
The distinction between even and odd numbers is a fundamental mathematical concept that enhances numerical understanding and analytical skills. By grasping these differences, students can better navigate mathematical operations and patterns, applying this knowledge to both academic and real-world scenarios. This article aims to equip educators with the tools to effectively teach and students to confidently understand and utilize these essential numerical properties.
Share :
