Factors of 26, Prime Factors of 26, How to Calculate, Tips
The factors of a number is a fundamental concept in mathematics. Factors of a number are the integers that can be multiplied together to produce that number. For instance, the number 26 has several factors, both positive and negative. Knowing these factors can be useful in various mathematical applications, including problem-solving and algebra. In this article, we will explore the factors of 26, how to calculate them, and their significance. Whether you’re a student looking to grasp basic math concepts or someone interested in number theory, this guide will provide you with a clear understanding of the factors of 26.
What are the Factors of 26?
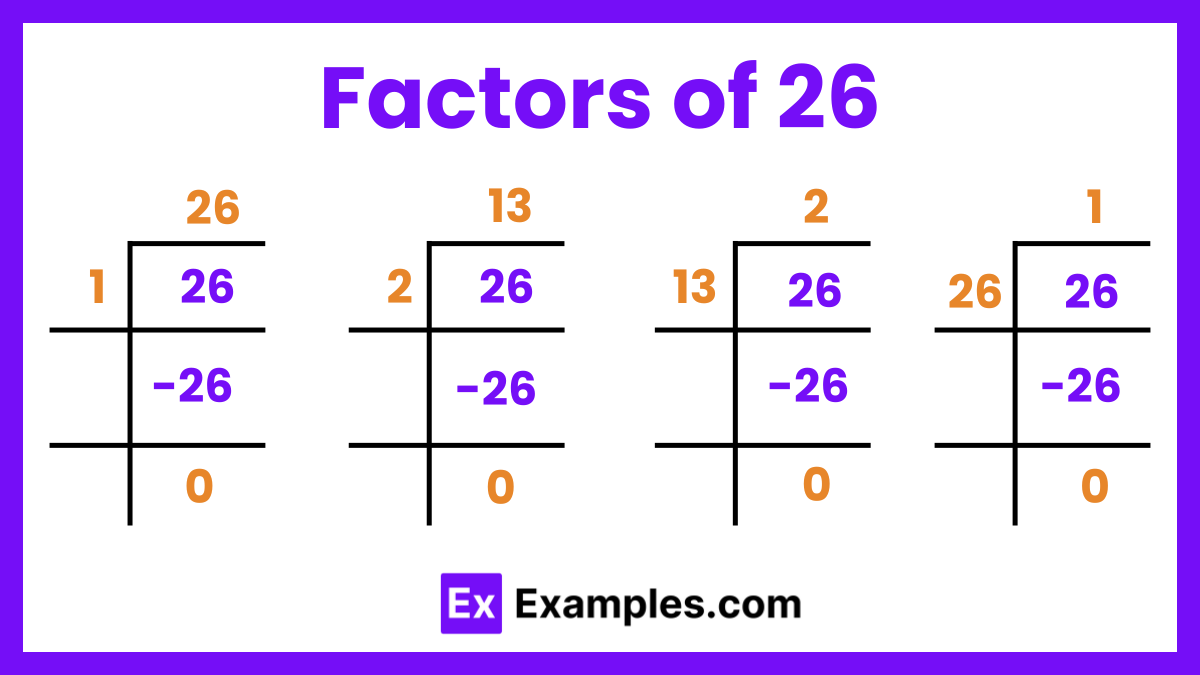
The factors of 26 are the numbers that divide 26 exactly without leaving a remainder. These factors include both positive and negative pairs. The positive factors of 26 are 1, 2, 13, and 26, as 1 x 26 and 2 x 13 both equal 26. Therefore, the negative factors of 26 are -1, -2, -13, and -26, because -1 x -26 and -2 x -13 also result in 26. Understanding these factors is crucial in various mathematical contexts, such as simplifying fractions, finding least common multiples, and solving algebraic equations.
Factors Pairs of 26
Factor pairs of 26 are sets of two numbers that, when multiplied together, equal 26. These pairs include both positive and negative integers. Understanding factor pairs is useful in many mathematical applications. Here are the factor pairs of 26:
- (1, 26): When multiplied, 1 and 26 give the product 26.
- (2, 13): Similarly, 2 and 13 also multiply to give 26.
- (-1, -26): The negative factors -1 and -26, when multiplied, result in 26 as well.
- (-2, -13): Lastly, -2 and -13 are another pair of negative factors that produce 26 when multiplied.
How to Calculate Prime Factors of 26
Calculating the prime factors of a number involves breaking it down into the prime numbers that multiply together to produce the original number. Prime factors are useful in various areas of mathematics, including simplifying fractions, finding least common multiples, and solving number problems. Here’s how you can calculate the prime factors of 26:
Step 1: Identify the Smallest Prime Number
Start by identifying the smallest prime number that can divide 26 without leaving a remainder. The smallest prime number is 2.
Step 2: Divide the Number by the Prime Number
Divide 26 by 2. Since 26 is an even number, it is divisible by 2. 26÷2=1326÷2=13
Step 3: Determine if the Resulting Quotient is Prime
After dividing, you get 13. Check if 13 is a prime number. A prime number has no divisors other than 1 and itself. Since 13 cannot be divided evenly by any number other than 1 and 13, it is a prime number.
Step 4: List All Prime Factors
Now that you have determined that 13 is a prime number, you can list the prime factors of 26. The prime factors of 26 are 2 and 13.
Factors of 26: Examples
Example 1: Finding All Factors
Problem: List all the factors of 26.
Solution: To find all the factors of 26, determine which numbers divide 26 exactly without leaving a remainder. These numbers are 1, 2, 13, and 26. Therefore, the factors of 26 are 1, 2, 13, and 26.
Example 2: Prime Factorization
Problem: What is the prime factorization of 26?
Solution: Start by dividing 26 by the smallest prime number, which is 2. 26÷2=13 Since 13 is a prime number, the prime factorization of 26 is: 26=2×13
Example 3: Pairing Factors
Problem: Find the factor pairs of 26.
Solution: The factor pairs are pairs of numbers that, when multiplied together, equal 26. These pairs are:
- (1, 26)
- (2, 13)
- (-1, -26)
- (-2, -13)
Example 4: Using Factors in a Fraction
Problem: Simplify the fraction 26/52.
Solution: Identify the greatest common factor (GCF) of 26 and 52, which is 26. Divide both the numerator and the denominator by their GCF: 26/52=26÷26/52÷26=1/2. The simplified fraction is 1/2.
Example 5: Checking Divisibility
Problem: Determine if 26 is divisible by 3.
Solution: To check if 26 is divisible by 3, divide 26 by 3 and check for a remainder. Since 26 divided by 3 equals approximately 8.67, which is not an integer, 26 is not divisible by 3.
Factors of 26 : Tips
Understanding and working with factors can greatly enhance your mathematical skills. Here are some useful tips for finding and using the factors of 26:
- Always start with the number 1 and the number itself. For 26, 1 and 26 are the most basic factors.
- Check divisibility by the smallest prime numbers first, such as 2, 3, and 5. For 26, since it is an even number, start with 2.
- After dividing by the smallest prime, continue dividing the quotient by the next smallest primes until you cannot divide evenly anymore.
- Remember that factors come in pairs. For 26, the pairs are (1, 26) and (2, 13).
- Negative factors are also important. For every positive factor pair, there is a corresponding negative pair. For 26, these include (-1, -26) and (-2, -13).
- Use factors to simplify fractions. For instance, knowing the factors of 26 can help reduce the fraction 26/52 to 1/2.
- Factors can help in finding the greatest common divisor (GCD) with other numbers, which is useful for simplifying mathematical expressions and solving problems.
- Understanding factors is essential for prime factorization, which breaks down a number into its prime components. For 26, the prime factors are 2 and 13.
- Knowing how to find and use factors can aid in solving a variety of mathematical problems, including those involving multiples, divisibility, and algebraic equations.
- Practice finding factors for different numbers to improve your proficiency and speed in recognizing factor pairs and prime factorizations.
How do you determine if a number is a factor of 26?
To determine if a number is a factor of 26, divide 26 by that number. If the result is an integer with no remainder, then the number is a factor of 26.
Are the factors of 26 related to its divisors?
Yes, factors and divisors are essentially the same. Both terms refer to numbers that can divide 26 exactly without leaving a remainder.
How do you find the factors of a number larger than 26?
To find the factors of a number larger than 26, use the same method: determine which numbers divide the larger number exactly without leaving a remainder. Repeat this process with all integers up to the square root of the number.
What are the positive and negative pair factors of 26?
The positive and negative pair factors of 26 are:
- Positive pairs: (1, 26) and (2, 13)
- Negative pairs: (-1, -26) and (-2, -13)
These pairs show that both positive and negative numbers can be factors, as long as their product equals 26.
How many factors does the number 26 have?
The number 26 has four factors: 1, 2, 13, and 26. These are the numbers that can divide 26 exactly without leaving a remainder. This includes both positive and negative factors.
What is the Sum of the Factors of 26?
The sum of the factors of 26 is 42. This is calculated by adding all the positive factors together:
1 + 2 + 13 + 26 = 42. The sum helps in understanding the properties of the number 26.


