Factors of 28, Prime Factors of 28, How to Calculate, Tips
The factors of a number is a fundamental concept in mathematics that aids in simplifying various calculations and solving problems efficiently. The factors of 28 are the numbers that can be multiplied together to result in 28, including 1, 2, 4, 7, 14, and 28. Recognizing these factors is crucial in reducing fractions, finding common multiples, and solving algebraic equations. For instance, knowing that 28 can be divided by these specific numbers helps in simplifying complex mathematical expressions. Additionally, understanding the factors of 28 is beneficial in real-world scenarios, such as dividing items into equal groups or organizing data. This guide will explore the factors of 28 in detail and demonstrate their practical applications.
What are the Factors of 28?
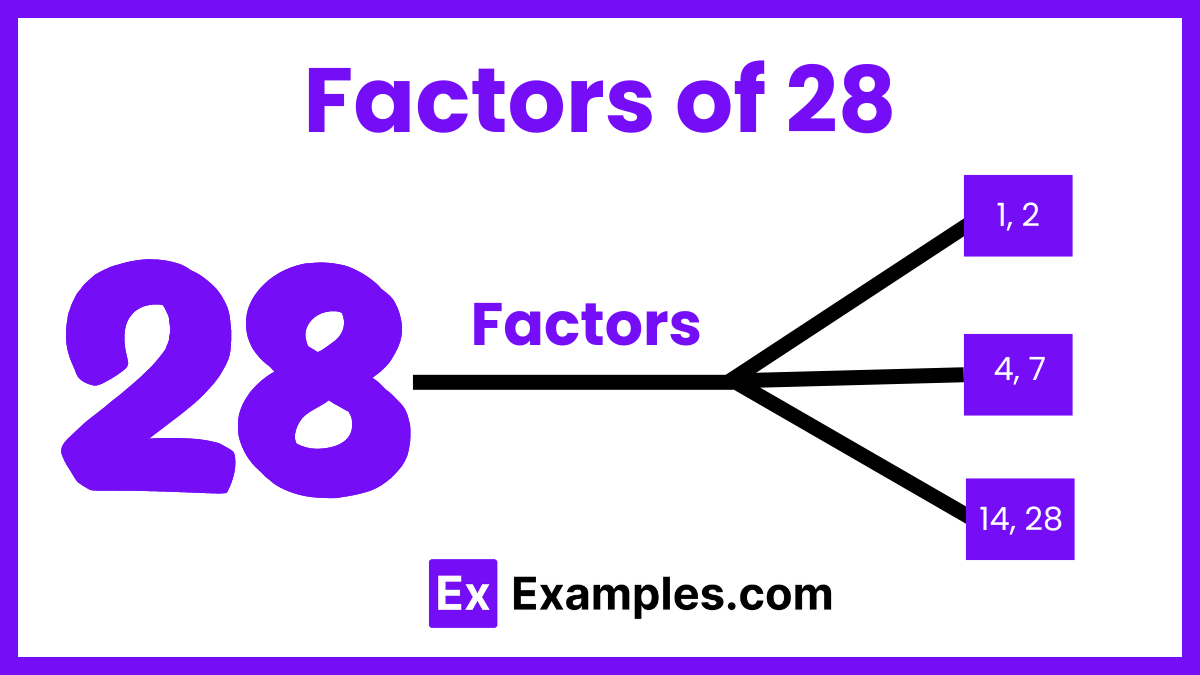
The factors of 28 are the numbers that divide it without leaving a remainder. These include 1, 2, 4, 7, 14, and 28. Understanding these factors is helpful in simplifying fractions, finding common multiples, and solving various mathematical problems. Knowing the factors of 28 can also aid in real-world applications like dividing objects into equal groups.
Factors Pairs of 28
- 1 and 28: The factor pair 1 and 28 multiplies to give 28. This is the most basic pair, showing that 1 is a factor of every number.
- 2 and 14: The factor pair 2 and 14 multiplies to give 28. This pair highlights that 28 is an even number and can be divided by 2.
- 4 and 7: The factor pair 4 and 7 multiplies to give 28. This pair is useful in various mathematical applications, such as simplifying fractions and solving problems involving multiplication and division.
How to Calculate Prime Factors of 28
Step 1: Start with the smallest prime number
Begin by dividing 28 by the smallest prime number, which is 2. Since 28 is even, it can be divided by 2. 28÷2=14
Step 2: Continue dividing by 2
Next, take the result from the first division (14) and divide it by 2 again. 14÷2=7
Step 3: Divide by the next smallest prime number
Now, take the result from the second division (7). Since 7 is a prime number and cannot be divided further by 2, check the next smallest prime number. In this case, 7 itself is a prime number. 7÷7=1
Step 4: Collect the prime factors
The division stops when the result is 1. The prime factors of 28 are the prime numbers you used in the divisions. So, the prime factors of 28 are 2, 2, and 7.
The prime factorization of 28 can be expressed as: 28=2×2×7 or 28=22×7
Factors of 28: Examples
Example 1: Simplifying a Fraction
Problem: Simplify the fraction 28/56.
Solution: Identify the common factors of 28 and 56. The greatest common factor (GCF) is 28.
Divide both the numerator and the denominator by 28. 28÷28/56÷28=1/2.
Example 2: Finding Common Factors
Problem: Find the common factors of 28 and 42.
Solution: List the factors of each number.
- Factors of 28: 1, 2, 4, 7, 14, 28
- Factors of 42: 1, 2, 3, 6, 7, 14, 21, 42
- The common factors are 1, 2, 7, and 14.
Example 3: Prime Factorization
Problem: Determine the prime factorization of 28.
Solution: Divide 28 by the smallest prime number, 2. 28÷2=14 Divide 14 by 2. 14÷2=7 Since 7 is a prime number, the prime factorization of 28 is: 28=2×2×7=22×7
Example 4: Finding the Least Common Multiple (LCM)
Problem: Find the LCM of 28 and 21.
Solution: List the prime factorizations.
Prime factors of 28: 22×7
Prime factors of 21: 3×7 The LCM is found by taking the highest power of all prime factors. LCM=22×3×7=4×3×7=84
Example 5: Solving an Equation
Problem: Solve for 𝑥 in the equation 4𝑥=28.
Solution: Divide both sides of the equation by 4. 4𝑥÷4=28÷4
x=7 .The solution is 𝑥=7x=7.
Factors of 28 : Tips
Understanding the factors of a number can greatly simplify many mathematical problems and real-world applications. Here are some tips to help you grasp the concept of factors, specifically for the number 28.
- List All Factors: Start by listing all the numbers that can divide 28 without leaving a remainder. These are 1, 2, 4, 7, 14, and 28.
- Use Division: To find factors, divide 28 by smaller numbers starting from 1 upwards. Any number that divides 28 exactly (without leaving a remainder) is a factor.
- Understand Prime Factors: Break down 28 into its prime factors by continuous division by the smallest prime numbers. For 28, the prime factors are 2 and 7, giving 28=22×728=22×7.
- Apply in Fractions: Simplify fractions involving 28 by using its factors. For instance, simplify 28565628 by dividing both the numerator and the denominator by 28.
- Real-World Applications: Use the factors of 28 to divide items into equal groups, calculate multiples, or solve practical problems such as distributing 28 objects equally.
- Check with Multiplication: Verify your list of factors by multiplying the pairs to see if they result in 28. For example, 4×7=284×7=28.
- Greatest Common Factor (GCF): When comparing 28 with another number, list the factors of both numbers to find their GCF. This is useful for simplifying ratios and solving problems involving multiple quantities.
- Least Common Multiple (LCM): Use the prime factors of 28 to find the LCM with another number. This is helpful in adding or subtracting fractions with different denominators.
- Visual Aids: Draw factor trees or use visual aids to break down 28 into its prime factors, making it easier to understand and remember.
- Practice: Regularly practice finding factors of different numbers, including 28, to strengthen your number sense and factorization skills.
Can 28 be a factor of another number?
Yes, 28 can be a factor of another number if that number can be divided by 28 without leaving a remainder. For example, 56 and 84 have 28 as a factor.
What is the difference between factors and multiples of 28?
Factors of 28 are numbers that divide evenly into 28, such as 1, 2, 4, 7, 14, and 28. Multiples of 28 are numbers that result from multiplying 28 by an integer, such as 28, 56, 84, and so on.
What is the greatest common factor (GCF) of 28 and 42?
The greatest common factor of 28 and 42 is 14. This is the largest number that can divide both 28 and 42 without leaving a remainder.
Are the factors of 28 are both positive and negative numbers?
Yes, Factors of 28 include both positive and negative numbers. The positive factors are 1, 2, 4, 7, 14, and 28, while the negative factors are -1, -2, -4, -7, -14, and -28.
How do the factors of 28 relate to its divisors?
The factors of 28 are the same as its divisors. A divisor is a number that divides another number without leaving a remainder, and factors are specific divisors of a given number.
What is the relationship between factors and prime factors of 28?
The factors of 28 include all numbers that divide 28 without leaving a remainder, while the prime factors are the prime numbers that multiply together to give 28. For 28, the prime factorization is 2 x 2 x 7.


