Circular Motion

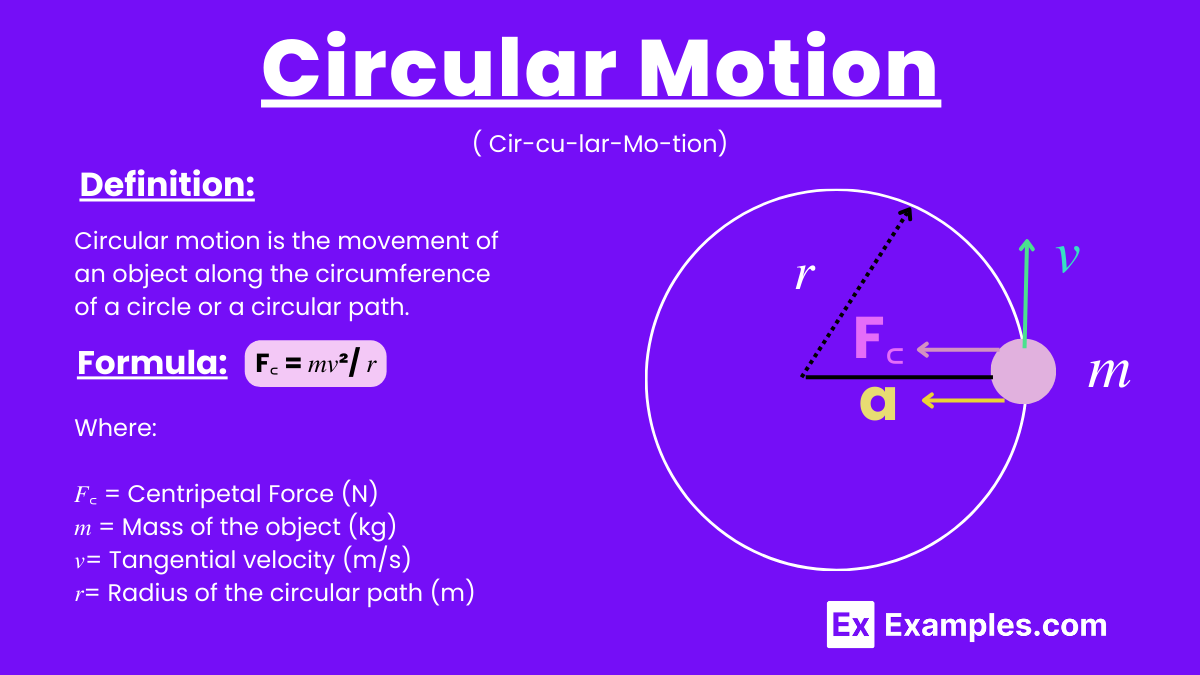
Circular motion refers to the movement of an object along the circumference of a circle or a circular path. In this type of motion, the object’s distance from a fixed central point remains constant while it travels around this point. The velocity of the object changes direction continuously, even if its speed remains constant, due to the centripetal force acting towards the center of the circle. This force is essential to maintain the circular trajectory, counteracting the object’s natural tendency to move in a straight line due to inertia. Circular motion is commonly observed in planetary orbits, the motion of a car around a curved track, and the rotation of a fan blade.

What Is Circular Motion?

Circular motion is the movement of an object along the circumference of a circle or a circular path. This motion involves a continuous change in direction, leading to centripetal acceleration towards the center of the circle, essential in understanding rotational dynamics.

Circular Motion Formulas

1. Centripetal Force (Fc)

F꜀ = 𝑚𝑣²/ 𝑟

Where:

𝐹꜀ = Centripetal Force (N)
𝑚 = Mass of the object (kg)
𝑣= Tangential velocity (m/s)
𝑟= Radius of the circular path (m)

2. Centripetal Acceleration (ac) :

a꜀ = v²/r

Where:

a꜀= Centripetal Acceleration (m/s²)
v = Tangential velocity (m/s)
r = Radius of the circular path (m)

3. Tangential Velocity (v)

v = ωr

Where:

• v = Tangential velocity (m/s)
• ω = Angular velocity (rad/s)
• r = Radius of the circular path (m)

4. Angular Velocity (ω)

ω= θ/ t

Where:

• ω = Angular velocity (rad/s)
• θ = Angular displacement (rad)
• t = Time (s)

5. Period of Revolution (T)

T = 2πr​/ v

Where:

• T = Period of revolution (s)
• r = Radius of the circular path (m)
• v = Tangential velocity (m/s)

6. Frequency of Revolution (f)

f= 1/ T=v / 2πr

Where:

• f = Frequency of revolution (Hz)
• T = Period of revolution (s)
• v = Tangential velocity (m/s)
• r = Radius of the circular path (m)

Applications of Circular Motion Formulas

Understanding these formulas is crucial for analyzing various real-world scenarios involving circular motion, such as:

• Planetary Orbits: Calculating the centripetal force keeping planets in orbit around the sun.
• Car Turning on a Curved Path: Determining the necessary frictional force to prevent skidding.
• Rotational Machinery: Evaluating the forces in rotating parts to ensure mechanical stability.

Examples of Circular Motion

1. Spinning Wheels: The wheels of bicycles and cars rotate in circular motion.
2. Ceiling Fans: Blades of ceiling fans rotate around a central hub.
3. Clock Hands: The hands of analog clocks move in a circular path.
4. CDs and DVDs: When played, they spin around their center.
5. Merry-Go-Rounds: Seats move in a circle around a central axis.
6. Figure Skating Spins: Skaters spin in circles during routines.
7. Gymnasts on Rings: Gymnasts rotate their bodies around the rings.
8. Basketball Spinning: The ball spins in circular motion during a free throw.
9. Hammer Throw: Athletes spin the hammer in a circular path before releasing it.
10. Hula Hooping: The hoop moves in a circular motion around the waist.
11. Planetary Orbits: Planets move in elliptical orbits around the sun.
12. Moon’s Orbit: The moon revolves around Earth.
13. Water in a Drain: Water spirals down a drain in a circular motion.
14. Whirlpools and Tornadoes: Water and air rotate around a central vortex.
15. Electron Orbits: Electrons move in circular orbits around the nucleus of an atom.
16. Electric Motors: Rotors inside electric motors spin to create movement.
17. Hard Disk Drives: The platters inside spin at high speeds.
18. Washing Machines: The drum rotates during the spin cycle.
19. Wind Turbines: The blades rotate to generate electricity.
20. Rotary Blades: Blades in helicopters rotate to provide lift.

Circular Motion Examples for Class 9

1. Tires on a Moving Car: As a car moves, its tires rotate in a circular motion.
2. Washing Machine Drum: During the spin cycle, the drum of a washing machine spins in a circular path.
3. Yo-Yo: When you spin a yo-yo, it moves up and down in a circular motion.
4. Rotating Sprinkler: Garden sprinklers often rotate in a circular pattern to distribute water evenly.
5. Wind Turbines: The blades of wind turbines rotate in a circular motion to generate electricity.
6. Gyroscope: Gyroscopes maintain orientation by spinning in a circular motion.
7. Crankshafts in Engines: The crankshaft in an internal combustion engine rotates in a circular motion.
8. Rotary Tools: Tools like drills and dremels rotate in circular motion to perform tasks.
9. Helicopter Rotors: The main rotor blades of a helicopter spin in a circular path to provide lift.
10. Potter’s Wheel: A potter’s wheel rotates in a circular motion to shape clay.
11. Circular Saws: The blade of a circular saw spins to cut through materials.
12. Wheels of a Skateboard: The wheels of a skateboard turn in a circular motion as it moves.
13. Amusement Park Rotors: Rotor rides in amusement parks spin in a circular path.
14. Rotating Beacons: Emergency vehicle lights often rotate in a circular pattern to signal their presence.
15. Spinning Frisbee: When you throw a frisbee, it spins in a circular motion through the air.
16. Drone Propellers: The propellers of drones rotate in circular paths to provide lift and control.
17. Earth’s Rotation: The Earth itself rotates in a circular motion around its axis.
18. Vortex in Fluids: When water drains, it creates a circular vortex.
19. Roller Bearings: The rollers in bearings move in circular paths to reduce friction.
20. Pulleys in Machinery: Pulleys rotate in a circular motion to lift or move loads.

Types of Circular Motion

Circular motion is a fundamental concept in physics, describing the motion of an object along the circumference of a circle. This motion can be categorized based on several criteria. Below are the primary types of circular motion:

1. Uniform Circular Motion (UCM)
   • Occurs when an object moves in a circle with a constant speed.
   • Characteristics:
     • Constant speed: The magnitude of the velocity remains constant.
     • Changing velocity: The direction of the velocity changes continuously, resulting in acceleration.
     • Centripetal force: This inward force is necessary to keep the object moving in a circle and is directed towards the center of the circle.
   • Examples:
     • A car turning around a circular track at a constant speed.
     • The motion of a satellite orbiting Earth in a circular path.
2. Non-Uniform Circular Motion
   • Occurs when an object moves in a circle with a varying speed.
   • Characteristics:
     • Variable speed: The speed of the object changes over time.
     • Changing velocity and acceleration: Both the magnitude and direction of the velocity change, leading to variable acceleration.
     • Centripetal and tangential forces: The object experiences both centripetal force (directed towards the center) and tangential force (acting along the tangent to the path).
   • Examples:
     • A car accelerating or decelerating while turning around a circular track.
     • A roller coaster moving through a circular loop with varying speed.
3. Horizontal Circular Motion
   • Refers to the motion of an object moving in a circular path in a horizontal plane.
   • Characteristics:
     • Constant height: The object remains at the same height above the ground.
     • Centripetal force: Provided by friction, tension, or other horizontal forces.
   • Examples:
     • A car turning on a flat, circular track.
     • A ball tied to a string and swung in a horizontal circle.
4. Vertical Circular Motion
   • Describes the motion of an object moving in a circular path in a vertical plane.
   • Characteristics:
     • Variable speed: Speed changes due to the influence of gravity.
     • Centripetal force: Combination of tension (or normal force) and gravitational force.
     • Critical points: Speed and tension vary significantly at the top and bottom of the path.
   • Examples:
     • A roller coaster performing a vertical loop.
     • A bucket of water swung in a vertical circle.
5. Rotational Motion
   • Occurs when an object spins around an internal axis.
   • Characteristics:
     • Fixed axis: The object rotates around a fixed point or axis within itself.
     • Angular displacement: Measured in radians, describing how far the object has rotated.
   • Examples:
     • The spinning of a top.
     • The rotation of the Earth on its axis.

Difference between Uniform and non-Uniform Circular Motion

Aspect	Uniform Circular Motion	Non-Uniform Circular Motion
Speed	Constant	Variable
Acceleration	Centripetal acceleration only	Both centripetal and tangential accelerations
Velocity	Constant magnitude, changing direction	Changing magnitude and direction
Force	Constant magnitude, directed towards the center	Variable magnitude and direction
Examples	Earth orbiting the Sun	Car accelerating/decelerating in a circular track
Angular Velocity	Constant	Variable

Applications of Circular Motion

Circular motion plays a vital role in various natural phenomena and technological advancements. Here are some significant applications:

1. Artificial Satellites

• Communication: Satellites enable global communication, broadcasting signals for television, radio, and internet services.
• Weather Forecasting: Meteorological satellites monitor weather patterns and predict natural disasters.
• GPS: Global Positioning System satellites provide accurate location data for navigation.

2. Planetary Motion

• Orbiting Planets: Planets revolve around the Sun in nearly circular orbits due to the gravitational force acting as the centripetal force.

3. Amusement Park Rides

• Ferris Wheel: Passengers move in a vertical circle, experiencing varying forces at different points.
• Roller Coaster: Combines circular and projectile motion to create thrilling experiences.
• Merry-Go-Round: Rotates around a central axis, providing circular motion for riders.

4. Centrifuges

• Medical Laboratories: Used to separate blood components or purify samples.
• Industrial Applications: Employed to separate liquids and solids in chemical processes.

5. Automobile Tires

• Turning and Maneuvering: Tires undergo circular motion when a car turns, with friction providing the necessary centripetal force.

6. Engine Flywheels

• Energy Storage: Flywheels store rotational energy through circular motion, maintaining consistent engine speed and smooth power delivery.

7. Electric Generators and Motors

• Electric Generators: Convert mechanical energy into electrical energy through rotational motion.
• Electric Motors: Convert electrical energy into mechanical energy using principles of circular motion.

8. Washing Machines

• Spin Cycle: Uses circular motion to remove water from clothes by spinning them at high speeds.

Practice Problems on Circular Motion

Problem 1: Centripetal Force Calculation

A car of mass 1,000 kg is traveling at a speed of 20 m/s around a circular track with a radius of 50 meters. Calculate the centripetal force acting on the car.

Solution:

• Given:
  • Mass (m) = 1,000 kg
  • Speed (v) = 20 m/s
  • Radius (r) = 50 m
  • Formula: F꜀ = 𝑚𝑣²/ 𝑟
  • Substitute values in above formula

Answer: The centripetal force acting on the car is 8,000 N.

Problem 2: Angular Velocity Calculation

A wheel rotates 360 degrees (or 2𝜋 radians) in 4 seconds. Calculate its angular velocity.

Solution:

Given:
Angular displacement (𝜃) =2π radians
Time (t) = 4 seconds
Formula: ω= θ/ t
Substitute values in above formula

Answer: The angular velocity of the wheel is π/2 rad/s.

FAQ’s