Which of the following is the formula for circular velocity?
v = 2πr/T
v = πr²/T
v = r²/T
v = r/T
of 10
Circular Velocity Formula
Circular Velocity Formula
What is Circular Velocity Formula?
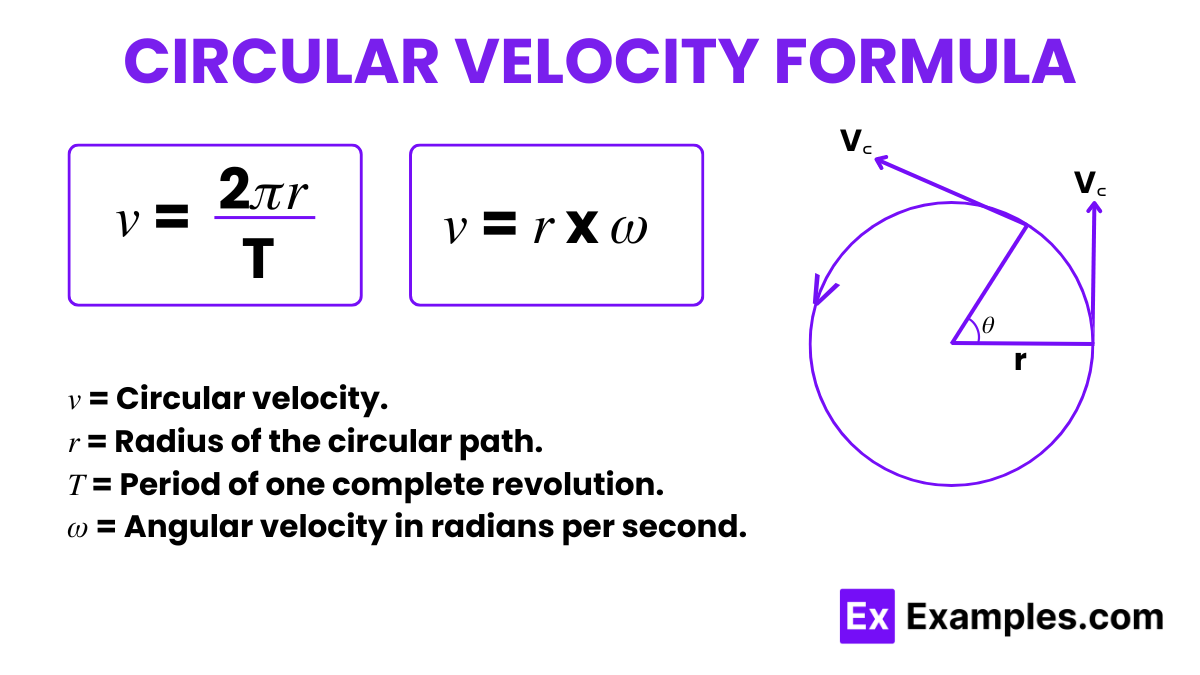
Circular velocity is a fundamental concept in physics that describes the velocity of an object moving along a circular path. The formula for circular velocity helps determine the speed at which an object must travel to maintain its circular trajectory without deviating from its path. This calculation is crucial in fields such as astronomy, engineering, and physics, where understanding motion in circular paths is essential.
The circular velocity formula is given by
- ๐ฃ is the circular velocity.
- ๐ is the radius of the circular path.
- ๐ is the period of one complete revolution.
- ๐ is the angular velocity in radians per second.
The formula can be understood as the distance covered per unit of time along a circular path. The first version of the formula relates the circumference of the circle ( 2๐r ) to the period ๐, which is the time it takes for one complete revolution. The second version uses angular velocity ๐, which links how fast the angle changes with the radius to find the linear velocity.
The concept of circular motion and its mathematical formulation have been explored by several physicists, but a precise “discovery” of the formula itself is more a development of collective work rather than a single discoverer’s breakthrough. Sir Isaac Newton’s laws of motion and universal gravitation, however, laid the groundwork for what we understand about circular motion today, including the derivation of the circular velocity formula through his second law of motion applied to celestial and terrestrial objects.
Application of Circular Velocity Formula
- Astronomy: Astronomers use the formula to calculate the speeds of planets and stars as they orbit around each other. Understanding these speeds helps in studying the dynamics of celestial systems.
- Satellite Communication: Engineers apply the formula to determine the velocity satellites must maintain to orbit the Earth. This ensures constant communication and correct positioning of satellites.
- Amusement Park Rides: Designers of roller coasters and other Circular rides use this formula to ensure these rides operate safely and provide the desired thrills without risking the safety of passengers.
- Particle Accelerators: Scientists use the circular velocity formula in particle accelerators to control the speed of particles moving in circular paths, crucial for experiments in particle physics.
- Automotive Industry: In vehicle dynamics, the formula helps in designing curved tracks and Roundabouts, Ensuring vehicles can pass through safely at appropriate speeds.
Example Problems on Circular Velocity Formula
Example 1: Calculating the Circular Velocity of a Satellite
Problem: A satellite orbits Earth at a radius of 42,000 Kilometers. If it takes the satellite 24 hours to complete one orbit, what is its Circular Velocity?
Solution:
Convert the orbital period from hours to seconds: 24 Hoursร3600 Seconds/hour=86,400 seconds
Use the Circular Velocity formula ๐ฃ = 2๐๐ / ๐โ:
๐ = 42,000 km = 42,000,000 meters
๐=86,400 seconds
๐ฃ=2๐ร42,000,00086,400 โ 3,052 meters/second
Answer: The Satelliteโs Circular Velocity is approximately 3,052 meters/second.
Example 2: Speed of a Racing Car on a Circular Track
Problem: A racing car is on a Circular track of 300 meters radius. If the car Completes one lap in 45 seconds, find its circular velocity.
Solution:
Apply the formula ๐ฃ=2๐๐ / ๐โ:
๐=300 meters
๐=45 seconds
๐ฃ=2๐ร30045โ42 meters/second
Answer: The carโs Circular Velocity is approximately 42 meters/second.
Example 3: Angular Velocity of a Ferris Wheel
Problem: A Ferris wheel has a Diameter of 50 meters and takes 2 minutes to complete one Rotation. Calculate the Circular Velocity of a cabin at the rim of the wheel.
Solution:
First, find the radius of the Ferris wheel (half the Diameter): ๐=25 meters.
Convert the Rotation time to seconds: ๐=2 minutesร60 seconds/minute=120 seconds.
Use the formula ๐ฃ=2๐๐ / ๐โ:
๐ฃ=2๐ร25120 โ 1.31 meters/second
Answer: The Circular Velocity of a cabin at the rim of the Ferris wheel is approximately 1.31 meters/second.
FAQs
What is the Formula for V in Circular Motion?
The formula for velocity (V) in circular motion is ๐=2๐๐ / ๐ or ๐=๐๐, where ๐ is radius and ๐ฯ is angular velocity.
Is Velocity the Same in Circular Motion?
No, velocity in circular motion varies as direction changes constantly, even if the speed (magnitude) remains constant.
What is the Formula for the Minimum Velocity of Circular Motion?
The minimum velocity formula in circular motion for maintaining the path is ๐๐๐๐ = โ๐๐โ, where ๐ is radius and ๐ is gravitational acceleration.
Share :
Practice Test
What does 'r' represent in the circular velocity formula v = 2πr/T?
Radius of the circle
Time period
Velocity
Angular displacement
of 10
What does 'T' represent in the formula v = 2πr/T?
Temperature
Tension
Time period
Torque
of 10
If the radius (r) is doubled, what happens to the circular velocity (v)?
It remains the same
It is halved
It doubles
It quadruples
of 10
How is the circular velocity affected if the time period (T) is halved?
It is halved
It doubles
It remains the same
It becomes zero
of 10
What is the unit of circular velocity in the SI system?
meters per second (m/s)
kilometers per hour (km/h)
miles per hour (mph)
feet per second (ft/s)
of 10
What happens to the circular velocity if the radius (r) is kept constant but the period (T) increases?
It increases
It decreases
It remains the same
It becomes infinite
of 10
How is the frequency (f) related to the period (T) in circular motion?
f = T²
f = 1/T
f = T
f = 2πT
of 10
If the frequency (f) of circular motion is known, how can you express the circular velocity (v)?
v = 2πrf
v = πrf
v = rf²
v = r/2πf
of 10
What is the angular velocity (ω) in terms of the period (T)?
ω = 2πT
ω = 2π/T
ω = πT
ω = T/2π
of 10