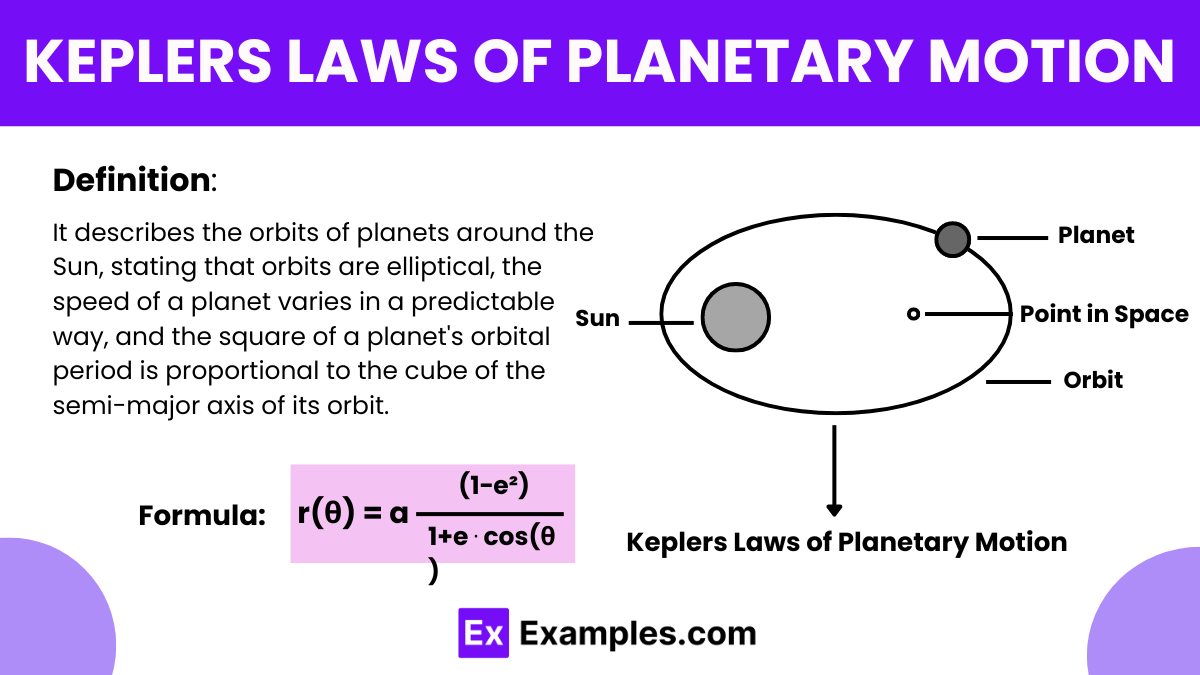
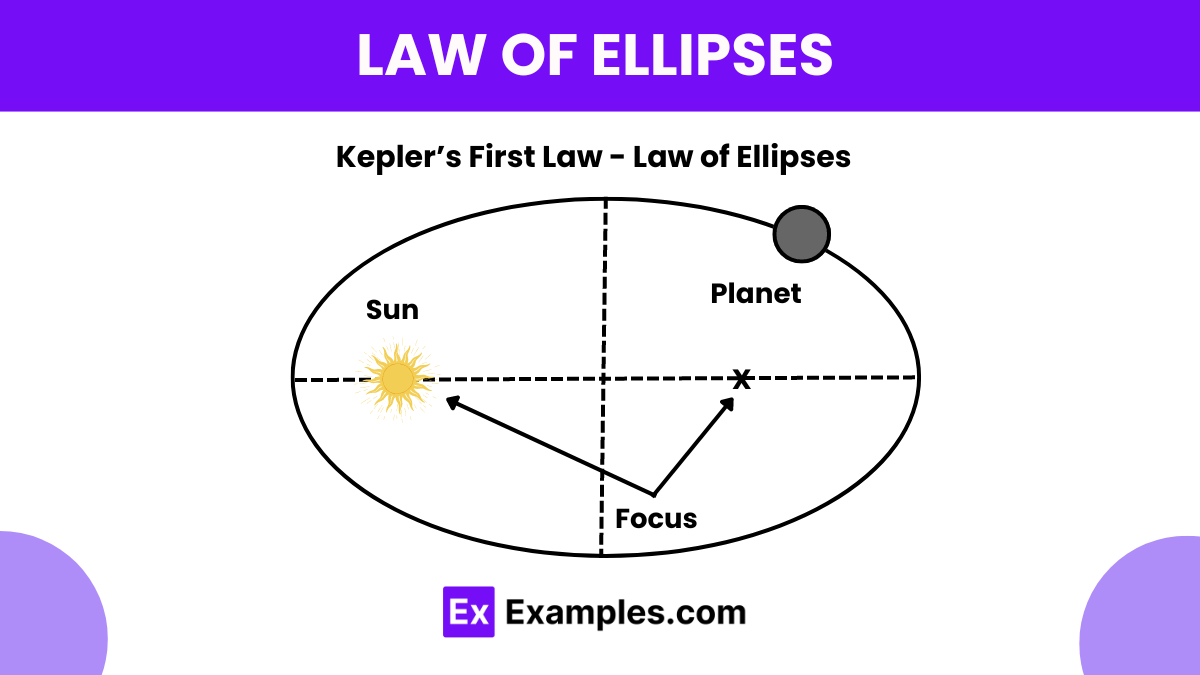
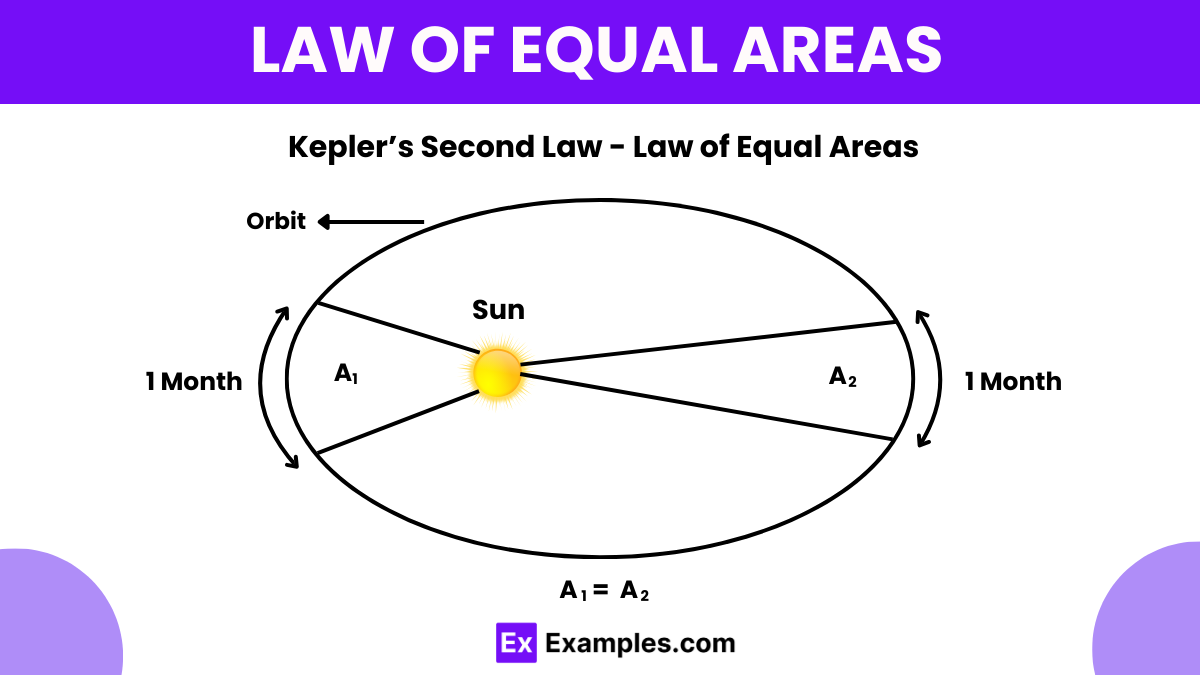
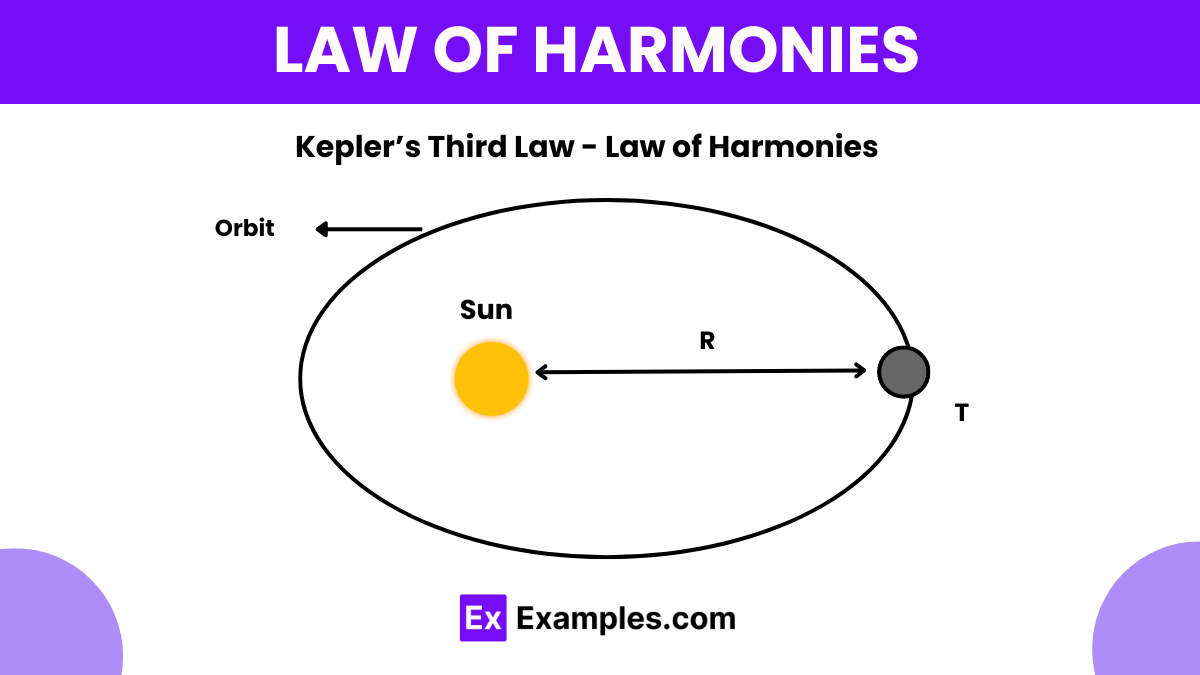
What does Kepler's First Law of Planetary Motion state?
Planets orbit in circular paths
Planets orbit in elliptical paths with the Sun at one focus
Planets move at a constant speed in their orbits
The square of the orbital period is proportional to the cube of the semi-major axis