Cubic meter
Cubic meter
What is Cubic meter?
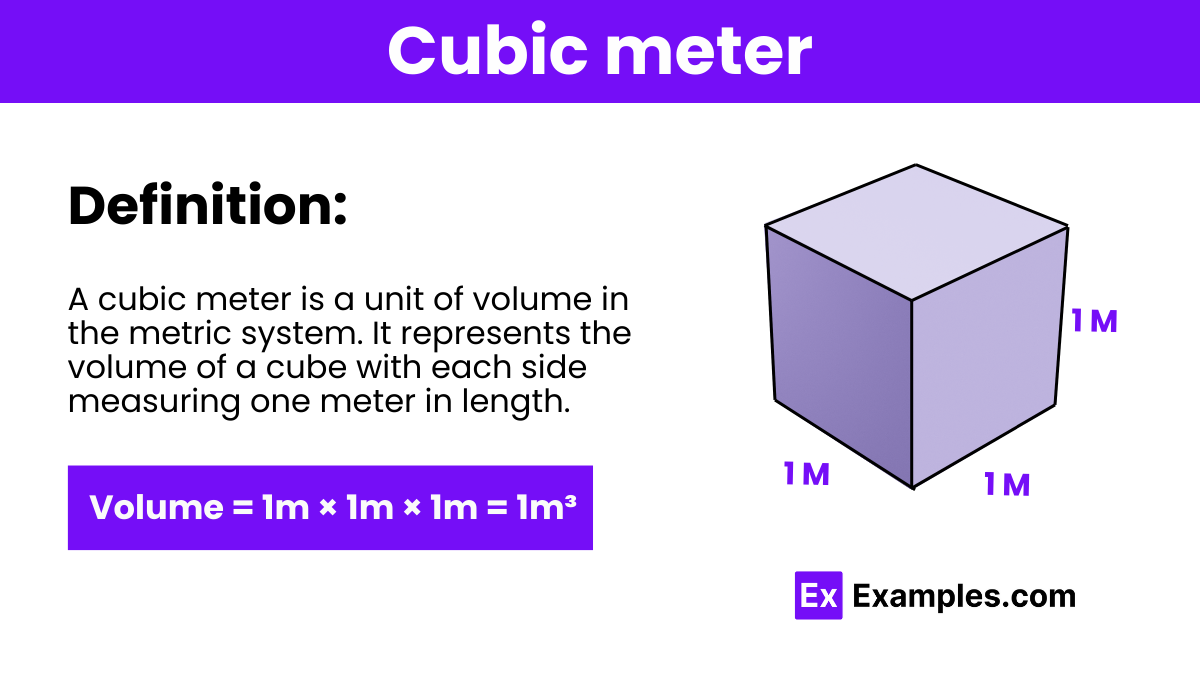
A cubic meter is a unit of volume in the metric system. It represents the volume of a cube that measures one meter on each side. It is commonly abbreviated as “m³“. One cubic meter is equivalent to 1,000 liters or 1,000,000 cubic centimeters. It’s used to measure the volume of large objects or quantities of substances like liquids, gases, or solids.
Unit of Cubic meter
The unit of measurement for volume represented by cubic meter is abbreviated as “m³” and is read as “cubic meters.
Cubic meter of 3D Shapes
Cube: A cube is a six-faced geometric shape where all sides are equal in length. The volume of a cube is calculated, where “s” is the length of the side. using the formula
Rectangular Prism: A rectangular prism is a six-faced shape with all rectangular faces. Its volume is calculated , where “l” is the length, “w” is the width, and “h” is the height. using the formula
Cylinder: A cylinder has two circular faces and a curved surface. The volume of a cylinder is calculated, where “r” is the radius of the circular base and “h” is the height. using the formula
Sphere: A sphere is a perfectly round geometrical object in three-dimensional space. The volume of a sphere is calculated, where “r” is the radius. using the formula
Cone: A cone has a circular base connected to a single vertex. Its volume is calculated, where “r” is the radius of the circular base and “h” is the height. using the formula
Pyramid: A pyramid has a polygonal base and triangular faces that meet at a common point called the apex. The volume of a pyramid is calculated , where “B” is the area of the base and “h” is the height. using the formula
List of Cubic meter Formulas
| Shape | Formula for Volume (V) |
|---|---|
| Cube | V = s³ |
| Rectangular Prism | V = l × w × h |
| Cylinder | V = πr²h |
| Sphere | V = 4/3 πr³ |
| Cone | V = 1/3 πr²h |
| Pyramid | V = 1/3 B h |
Conversion of Cubic meter into Other Units
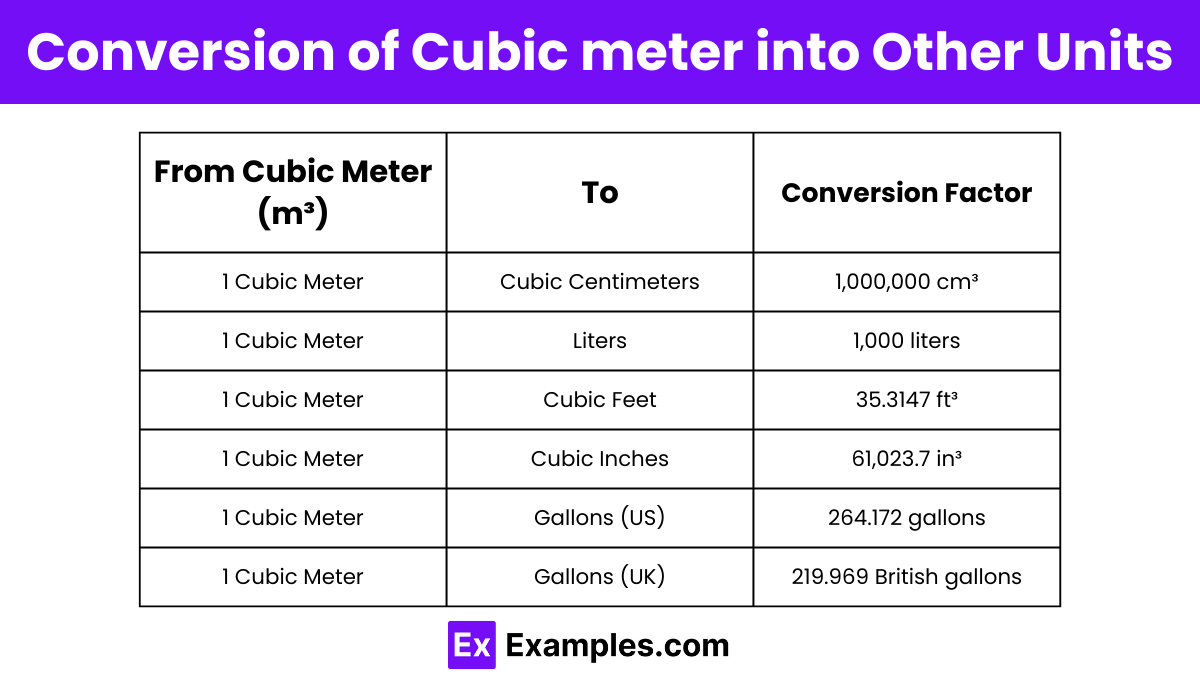
| From Cubic Meter (m³) | To | Conversion Factor |
|---|---|---|
| 1 Cubic Meter | Cubic Centimeters | 1,000,000 cm³ |
| 1 Cubic Meter | Liters | 1,000 liters |
| 1 Cubic Meter | Cubic Feet | 35.3147 ft³ |
| 1 Cubic Meter | Cubic Inches | 61,023.7 in³ |
| 1 Cubic Meter | Gallons (US) | 264.172 gallons |
| 1 Cubic Meter | Gallons (UK) | 219.969 British gallons |
Cubic Meters to Cubic Centimeters
This conversion is useful for smaller volumes in scientific or technical contexts where precision is necessary. A cubic centimeter is a cube whose sides are all 1 centimeter long.
Cubic Meters to Liters
Since a liter is defined as the volume of a cube that is 10 centimeters on a side, converting cubic meters to liters is straightforward. This conversion is common in everyday uses like measuring water.
Cubic Meters to Cubic Feet
Used predominantly in the United States and the UK for non-metric volume measurements in construction and appliance capacities. A cubic foot is a cube with each side measuring one foot.
Cubic Meters to Cubic Inches
Important for industries that use the imperial system, like manufacturing and automotive sectors. A cubic inch is a cube that is one inch on each side.
Cubic Meters to Gallons (US)
Commonly used in the United States for measuring larger volumes of liquids, like water and gasoline. The US gallon is used over the imperial gallon in American commerce.
Cubic Meters to Gallons (UK)
Used in the UK, this conversion helps measure volumes in scenarios where the British imperial system is still in use, like in fuel economy and some agricultural settings.
How to Calculate the Cubic meter?
- Identify the Shape: Determine the shape of the object whose volume you want to calculate. It could be a cube, rectangular prism, cylinder, sphere, cone, or pyramid.
- Gather Measurements: Measure the necessary dimensions required to calculate the volume of the specific shape. These measurements could include the side length, width, height, or radius, depending on the shape.
- Use the Correct Formula: Use the appropriate formula for the shape you are dealing with. Refer to the formulas provided earlier for each shape.
- Perform the Calculation: Substitute the measured values into the formula and perform the calculations. Make sure all units are consistent, typically in meters for cubic meters.
- Interpret the Result: The result of the calculation will be in cubic meters. This represents the volume of the object in terms of how many one-meter cubes can fit inside it.
- Round if Necessary: Depending on the precision required, you may need to round the result to an appropriate number of decimal places.
Difference between Cubic meter to Cubic Centimeter
| Measurement | Description | Conversion Factor |
|---|---|---|
| Cubic Meter (m³) | Volume unit in the metric system representing a cube with each side measuring one meter. | 1,000,000 cm³ |
| Cubic Centimeter (cm³) | Volume of a cube with each side measuring one centimeter. | 0.000001 m³ |
Example of Cubic meter
- Swimming Pool: A typical swimming pool might have dimensions of 10 meters in length, 5 meters in width, and 2 meters in depth, giving it a volume of 10×5×2 = 100 m³.
- Fish Tank: A large fish tank might have dimensions of 2 meters in length, 1 meter in width, and 1 meter in height, resulting in a volume of 2×1×1 = 2 m³.
- Room: A bedroom measuring 4 meters long, 3 meters wide, and 2.5 meters high would have a volume of 4×3×2.5 = 30 m³.
- Shipping Container: A standard shipping container typically measures 6 meters in length, 2.5 meters in width, and 2.5 meters in height, giving it a volume of 6×2.5×2.5 = 37.5 m³.
- Box: A cardboard box measuring 1 meter long, 0.5 meters wide, and 0.3 meters high would have a volume of 1×0.5×0.3 = 0.15 m³.
- Bathtub: A bathtub might measure 1.5 meters in length, 0.8 meters in width, and 0.6 meters in depth, resulting in a volume of 1.5×0.8×0.6 = 0.72 m³.
- Water Tank: A cylindrical water tank with a radius of 1 meter and a height of 3 meters would have a volume of π×12×3 = 3πm³.
- Grain Silo: A large grain silo with a diameter of 5 meters and a height of 10 meters would have a volume of 41×π×52×10 = 2125πm³.
- Concrete Block: A solid concrete block measuring 0.6 meters long, 0.4 meters wide, and 0.2 meters high would have a volume of 0.6×0.4×0.2 = 0.048 m³.
- Fuel Tank: An underground fuel tank with dimensions of 3 meters in diameter and 2 meters in height would have a volume of 1/4×π×3²×2 = 9/2π m³.
FAQs
How do you calculate cubic meters?
To calculate cubic meters, you typically multiply the length, width, and height of an object or space together. For irregularly shaped objects, you may need to use specific formulas for their respective shapes.
What are some common objects measured in cubic meters?
Common objects measured in cubic meters include swimming pools, rooms, shipping containers, fish tanks, water tanks, and grain silos, among others.
What is the difference between cubic meters and square meters?
Cubic meters measure volume, representing the amount of space an object or substance occupies in three dimensions (length, width, and height), while square meters measure area, representing the size of a two-dimensional surface.
How can I convert cubic meters to other units of volume?
You can convert cubic meters to other units such as liters, cubic centimeters, or cubic feet using conversion factors. For example, 1 cubic meter is equal to 1000 liters, 1,000,000 cubic centimeters, or approximately 35.31 cubic feet.
How do I estimate cubic meters for irregularly shaped objects?
For irregularly shaped objects, you can use methods such as water displacement or mathematical integration to estimate the volume. Alternatively, you can approximate the object’s volume by dividing it into smaller regular shapes and summing their volumes.
Share :
