Cos 37 Degrees

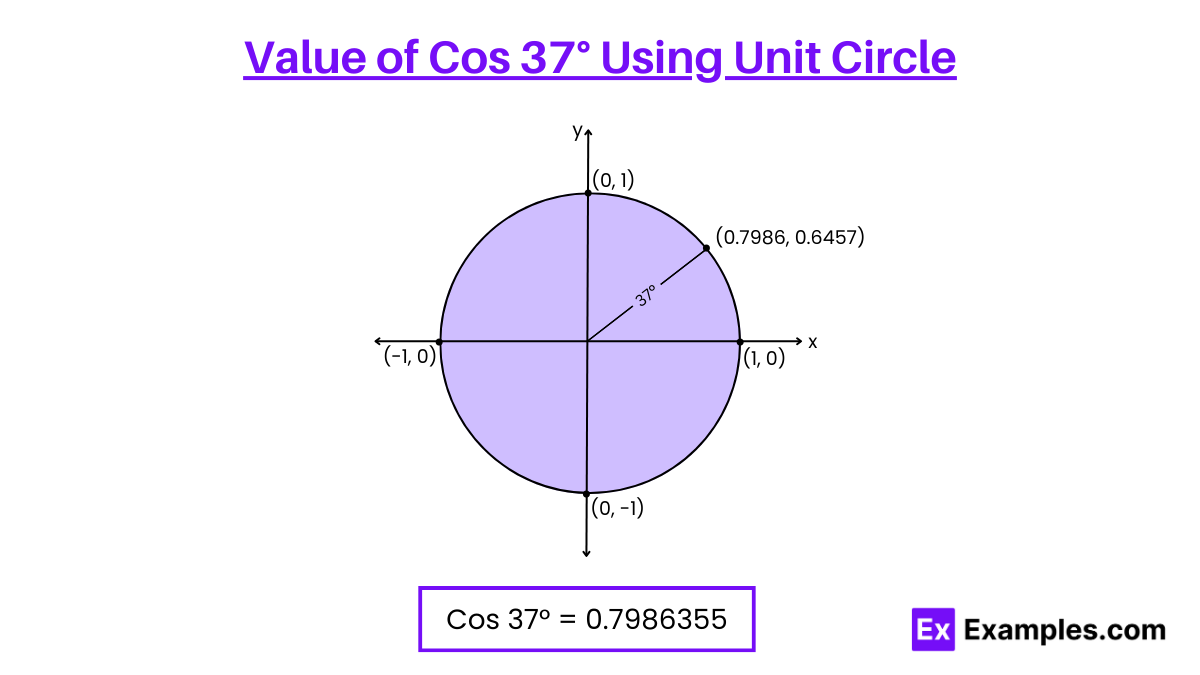
he value of cos 37 degrees is approximately 0.7986355. In radians, cos 37 degrees is written as cos (37° × π/180°), which is cos (0.6457718…). This article will discuss various methods to find the value of cos 37 degrees, with examples.

• Cos 37°: 0.7986355.
• Cos (-37°): 0.7986355, due to the even property of the cosine function.
• Cos 37° in Radians (37° × π/180°): cos (0.6457718…).

What is the Value of Cos 37 Degrees?

The cosine of 37 degrees is approximately:

• Cos 37° = 0.7986355

In radians, 37 degrees is converted using the formula: degrees × π/180.

• 37 degrees in radians = 37° × π/180 ≈ 0.6457718

So, in radians:

• Cos 37° = cos (0.6457718)

Methods to Find Value of Cos 37 Degrees

1. Using Trigonometric Functions
2. Using the Unit Circle

Using Trigonometric Identities

1. Pythagorean Identity

The Pythagorean identity relates the cosine and sine of an angle.

• Formula: Cos 37° = √(1 – sin² 37°)

Example:

If sin 37° is approximately 0.6018,

• Cos 37° = √(1 – 0.6018²) ≈ 0.7986

2. Tangent Function

The tangent function can also help in finding the cosine of an angle.

• Formula: Cos 37° = 1 / √(1 + tan² 37°)

Example:

If tan 37° is approximately 0.7536,

• Cos 37° = 1 / √(1 + 0.7536²) ≈ 0.7986

3. Cotangent Function

Cotangent, another trigonometric function, can be used as follows:

• Formula: Cos 37° = cot 37° / √(1 + cot² 37°)

Example:

If cot 37° is approximately 1.327,

• Cos 37° = 1.327 / √(1 + 1.327²) ≈ 0.7986

4. Cosecant Function

Cosecant provides another way to express cos 37 degrees:

• Formula: Cos 37° = √(cosec² 37° – 1) / cosec 37°

Example:

If cosec 37° is approximately 1.6629,

• Cos 37° = √(1.6629² – 1) / 1.6629 ≈ 0.7986

5. Secant Function

Finally, secant, the reciprocal of cosine, gives us a direct formula:

• Formula: Cos 37° = 1 / sec 37°

Example:

If sec 37° is approximately 1.251,

• Cos 37° = 1 / 1.251 ≈ 0.7986

Angle Relationships

Cos 37 degrees can be related to other angles using complementary and supplementary angle identities:

1. Supplementary Angles:
   • Cos 37° is equal to negative cos (180° minus 37°), which is negative cos 143°.
   • Formula: cos 37° = -cos (180° – 37°) = -cos 143°
2. Angles Beyond 180 Degrees:
   • Cos 37° is equal to negative cos (180° plus 37°), which is negative cos 217°.
   • Formula: cos 37° = -cos (180° + 37°) = -cos 217°
3. Complementary Angles:
   • Cos 37° is equal to the sine of 90° minus 37°, which is sine 53°.
   • Formula: cos 37° = sin (90° – 37°) = sin 53°
4. Angles Plus 90 Degrees:
   • Cos 37° is equal to the sine of 90° plus 37°, which is sine 127°.
   • Formula: cos 37° = sin (90° + 37°) = sin 127°

Practical Example

Example: Using the Pythagorean Identity

Given that sin 37° is approximately 0.6018, we can find cos 37°:

• Cos 37° is equal to the square root of 1 minus the sine squared of 37°.
• Cos 37° = √(1 – sin² 37°) = √(1 – 0.6018²) ≈ 0.7986

Cos 37 Degrees Using Unit Circle

Step 1: Understand the Unit Circle

• The unit circle has a radius of 1 and is centered at the origin (0, 0).
• It is divided by the x-axis and y-axis, which intersect the circle at four key points: (1, 0), (-1, 0), (0, 1), and (0, -1).

Step 2: Locate the Angle

• Identify the 37-degree angle on the unit circle. This angle starts from the positive x-axis and rotates counterclockwise.

Step 3: Find the Intersection Point

• Draw the terminal side of the 37-degree angle. This line intersects the unit circle.
• The coordinates of this intersection point represent the cosine and sine of 37 degrees.
• According to the image, the intersection point is approximately (0.7986, 0.6018).

Step 4: Determine the Cosine Value

• The x-coordinate of the intersection point is the value of cos 37°.
• From the image, cos 37° ≈ 0.7986.

Step 5: Confirm Positivity in the 1st Quadrant

• Since 37 degrees lies in the 1st quadrant, both cosine and sine values are positive.

Solved Problems

Problem 1: Verify Cos 37° using the Pythagorean identity

Solution:
We know that:
Sin 37° = 3/5
Using the Pythagorean identity:
Cos² 37° + Sin² 37° = 1
Substitute Sin 37°:
Cos² 37° + (3/5)² = 1
Cos² 37° + 9/25 = 1
Cos² 37° = 1 – 9/25
Cos² 37° = 25/25 – 9/25
Cos² 37° = 16/25
Cos 37° = 4/5

---

Problem 2: Use Cos 37° to find Sin 53°

Solution:
We know that:
Sin 53° = Cos (90° – 53°) = Cos 37°
Since we already know:
Cos 37° = 4/5
Therefore:
Sin 53° = 4/5

---

Problem 3: Calculate the value of 2Cos² 37° – 1

Solution:
First, calculate Cos² 37°:
Cos 37° = 4/5
Cos² 37° = (4/5)² = 16/25
Then, use the expression:
2Cos² 37° – 1 = 2 × 16/25 – 1
2Cos² 37° – 1 = 32/25 – 1
2Cos² 37° – 1 = 32/25 – 25/25
2Cos² 37° – 1 = 7/25

---

Problem 4: Find Cos 37° given Tan 37°

Solution:
We know:
Tan 37° = 3/4
Using the identity:
Tan x = Sin x / Cos x
Tan 37° = (3/5) / Cos 37°
We already know:
Cos 37° = 4/5

---

Problem 5: Use Cos 37° to find Cos 74°

Solution:
We know that:
Cos 74° = Cos (2 × 37°)
Using the double-angle identity:
Cos 2x = 2Cos² x – 1
Cos 74° = 2Cos² 37° – 1
We already calculated:
Cos² 37° = 16/25
So:
Cos 74° = 2 × 16/25 – 1
Cos 74° = 32/25 – 1
Cos 74° = 32/25 – 25/25
Cos 74° = 7/25
Cos 74° = 7/25

---