Square & Square Root of 66

Within algebraic mathematics, squares and square roots are fundamental concepts. Squaring a number, as seen with 66 (66² = 4356), involves multiplying the number by itself and is crucial for exploring rational and irrational numbers. Rational numbers can be expressed as fractions of integers, while irrational numbers cannot. Understanding these basics enriches mathematical comprehension and reveals intricate relationships and patterns.

Square of 66

66² (66 × 66) = 4356

The square of 66, a fundamental mathematical concept, yields 4356. This operation of multiplying a number by itself is essential for algebraic exploration and understanding properties of numbers, both rational and irrational. It helps reveal mathematical patterns and relationships.

Square Root of 66

√66 = 8.12403840464

The square root of 66, another fundamental mathematical concept, is approximately 8.12403840464. This value represents the number which, when multiplied by itself, equals 66. Mastery of square roots is crucial for understanding algebraic relationships and properties of both rational and irrational numbers, facilitating problem-solving across diverse domains.

Square Root of 66: 8.12403840464

Exponential Form: 66^½ or 66^0.5

Radical Form: √66

Is the Square Root of 66 Rational or Irrational?

The square root of 66 is an irrational number.

Irrational numbers cannot be expressed as a fraction of two integers and their decimal representations neither terminate nor repeat. Thus, √66 cannot be expressed as a simple fraction, and its decimal representation continues infinitely without repeating.

Examples of Rational and Irrational Numbers

Rational Numbers: 3/4, -5/2

Irrational Numbers: √2 (approximately 1.41421356…)

Methods to Find the Value of √66

• Prime Factorization Method: Since 66 is a product of prime factors (2, 3, and 11), and none form pairs, this method confirms the irrationality without providing an exact value.
• Estimation Method: Approximate √66 by finding perfect squares close to it. Since 66 is between 64 (8²) and 81 (9²), its square root is between 8 and 9. Refine the estimate using methods like Newton’s method.
• Long Division Method: This method finds the square root iteratively by dividing and averaging. It’s reliable for manual calculations.
• Calculator or Software: Use a calculator or software to directly compute √66. These tools have built-in functions for square roots.
• Continued Fraction Expansion: This method expresses √66 as a continued fraction and approximates its value by truncating the expansion.

Square Root of 66 by Long Division Method

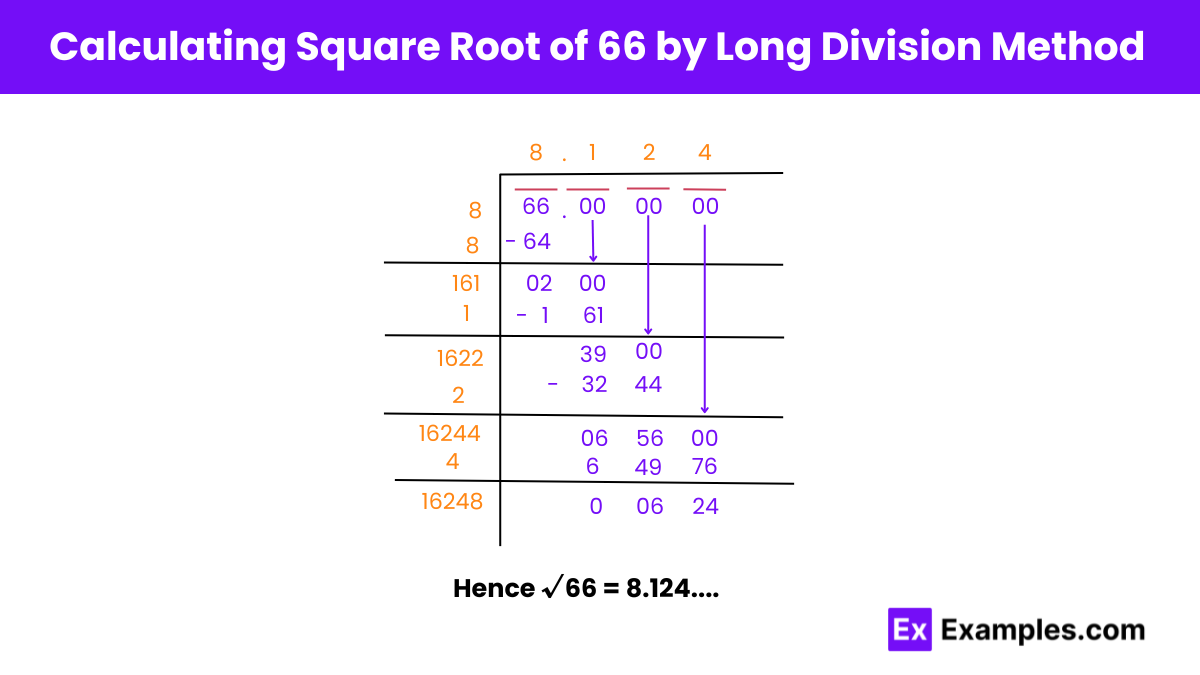
Setup and Initial Division:

• Pair the digits of 66 (66.000000) and find the largest number whose square is less than or equal to 66.
• ( 8 × 8 = 64 ). Place 8 in the quotient. Subtract 64 from 66, leaving a remainder of 2.

Form New Divisor and Bring Down Zeros:

• Double the quotient (8) to get 16.
• Bring down the next pair of zeros, making the new dividend 200. Find the largest digit ( n ) such that ( 16n × n ≤ 200 ). ( 161 × 1 = 161 ).

Repeat for Precision:

• Subtract 161 from 200, leaving a remainder of 39. Place 1 in the quotient.
• Bring down the next pair of zeros, making the new dividend 3900. Update the divisor to 162. Find ( n ) such that ( 162n × n ≤ 3900 ). ( 1622 × 2 = 3244 ).

Continue for More Digits:

• Subtract 3244 from 3900, leaving a remainder of 656. Place 2 in the quotient.
• Bring down the next pair of zeros, making the new dividend 65600. Update the divisor to 1624. Find ( n ) such that ( 1624n × n ≤ 65600 ). ( 16244 × 4 = 64976 ).

Final Steps:

• Subtract 64976 from 65600, leaving a remainder of 624. Place 4 in the quotient.
• The quotient now reads 8.124, which is the approximate value of √66.

Hence, √66 ≈ 8.124.

Is 66 a Perfect Square?

No, 66 is not a perfect square.

A perfect square is a number that can be expressed as the product of an integer with itself. For example, 9 is a perfect square because it equals 3 × 3. However, 66 cannot be expressed as the product of two equal integers, so it is not a perfect square.