square & square root of 37
square & square root of 37
Square of 37
The square numbers of 37, which is 1369, is derived by multiplying 37 by itself. This result signifies the area of a square with sides measuring 37 units each. It holds significance in mathematics, particularly in algebra and geometry. As a perfect square, it has unique properties, such as being the sum of consecutive odd numbers and having a digital root of 1.
Square Root of 37
or
√37 = 6.082
The square root of 37, approximately 6.08, is the number that, when multiplied by itself, equals 37. It’s an irrational number and can’t be expressed as a simple fraction.
Exponential Form: 37^½ or 37^0.5
Radical Form: √37
Is the Square Root of 37 Rational or Irrational?
An irrational number is a real number that cannot be expressed as a simple fraction, and its decimal representation goes on infinitely without repeating. When you calculate the square root of 37, you find that it cannot be represented as a terminating or repeating decimal. Instead, it goes on infinitely without a discernible pattern. This property distinguishes it from rational numbers, which can be expressed as fractions and have either terminating or repeating decimals. Since the square root of 37 falls into the category of numbers that cannot be expressed as fractions or finite decimals, it is considered irrational.
A rational number is any number that can be expressed as the quotient or fraction of two integers, where the denominator is not zero. In other words, a rational number can be written in the form 𝑎𝑏ba, where 𝑎a and 𝑏b are integers and 𝑏≠0. Rational numbers include integers and fractions, as well as terminating or repeating decimals.
Examples : 1/2 and 5.
An irrational numbers is a real number that cannot be expressed as a simple fraction, and its decimal representation goes on infinitely without repeating. In other words, it cannot be written as the quotient of two integers where the denominator is not zero. Irrational numbers include values like the square root of non-perfect squares or constants like π and e.
Examples : √2 ,√3
Methods to Find Value of Root 37
- Estimation: Use approximation techniques such as the Newton-Raphson method or trial and error to find an approximate value.
- Prime Factorization: Express 37 as a product of prime factors (37 is already a prime number), then take the square root of each prime factor and multiply them together.
- Decimal Approximation: Use a calculator or software to compute the decimal approximation of the square root of 37.
- Continued Fractions: Express the square root of 37 as a continued fraction to obtain a rational approximation.
- Algebraic Methods: Use algebraic techniques such as completing the square or using the quadratic formula to solve the equation 𝑥² = 37.
Square Root of 37 by Long Division Method
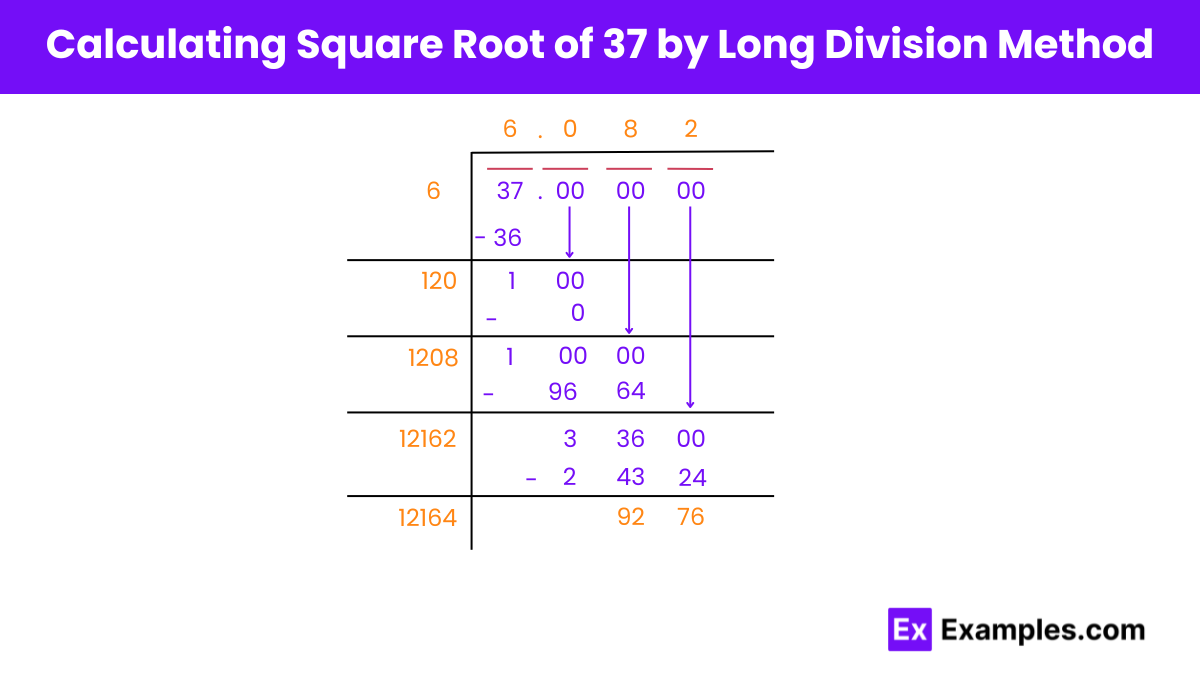
Step 1: Split 37 into pairs: 37.00 00 00.
Step 2: Find a number multiplied by itself that is less than or equal to 37. We find 6 × 6 = 36, leaving a remainder of 1.
Step 3: Bring down the first pair of zeros to form 100 as the new divisor.
Step 4: Place the decimal point after 6 in the quotient. Multiply the quotient by 2, resulting in 12x as the new divisor.
Step 5: Find a number for x such that 12x × x gives 100 or less. We find no such number, so we use 0. Subtract 120 × 0 from 100 to get a remainder of 10.
Step 6: Bring down the next pair of zeros to form 10000 as the new divisor.
Step 7: Multiply the quotient by 2, resulting in 120x as the new divisor.
Step 8: Find a number for x such that 120x × x gives 10 0000 or less. We find 1208 × 8 = 9664. Subtract this from 10 0000 to get a remainder of 336.
Step 9: Repeat the process until reaching the desired level of precision, such as approximating to 3 decimal places.
Step 10: Thus, the square root of 37 is approximately 6.082 to the nearest thousandths.
Is 37 Perfect Square root or Not
No, because its square root, which is approximately 6.082, is not an integer. A perfect square is a number that can be expressed as the square of an integer, whereas 37 cannot be expressed as the square of any integer.
FAQ’S
Can the square root of 37 be simplified?
No, the square root of 37 is an irrational number, so it cannot be expressed as a simplified fraction.
What are some properties of the square root of 37?
The square root of 37 is an irrational number, meaning its decimal representation goes on infinitely without repeating.
What applications involve the square root of 37?
he square root of 37 is used in mathematics, engineering, physics, and various other fields where calculations involving areas, distances, or volumes are necessary.
Why is the square root of 37 important?
The square root of 37, being an irrational number, demonstrates the infinite nature of real numbers and is fundamental in mathematical theory and problem-solving.
Share :
