Cos 2x

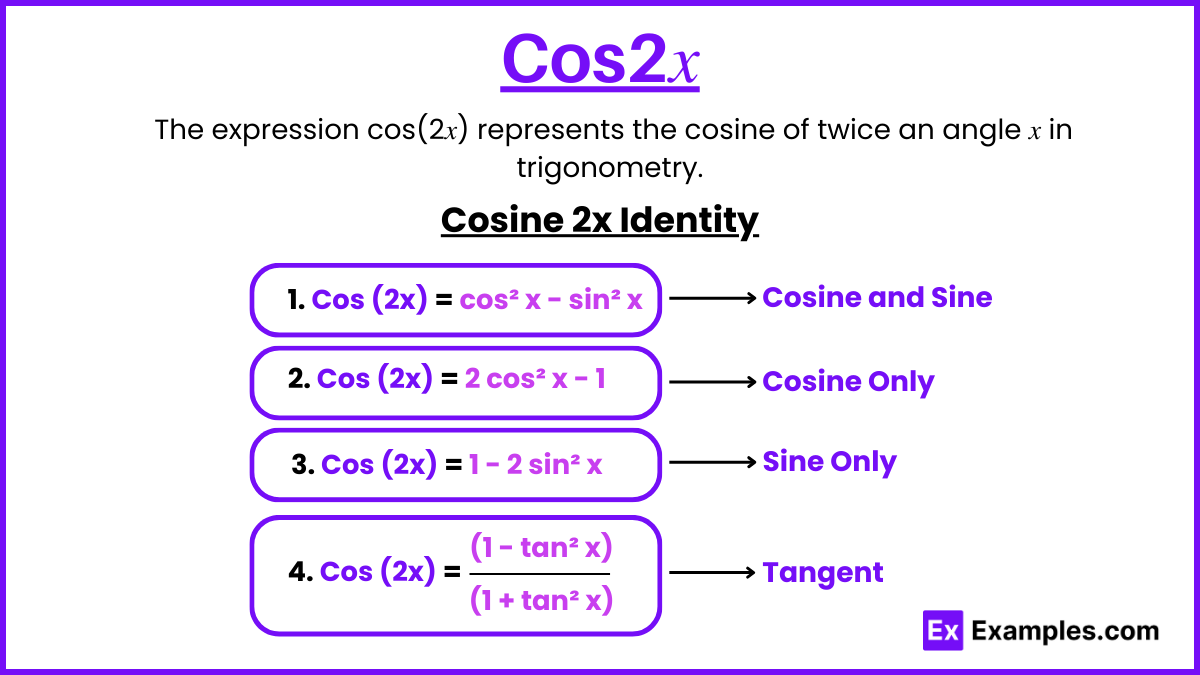
The cos2x identity is an essential trigonometric formula used to find the value of the cosine function for double angles, also known as the double angle identity of the cosine function. This identity helps express the cosine of a compound angle 2x in various ways: in terms of sine and cosine functions, only the cosine function, only the sine function, and only the tangent function. Derived using different trigonometric identities, the cos2x formula can be represented in multiple forms. Additionally, we will explore the concept of cos²x (cos square x) and its formula in detail.

What is Cos2x?

Cos2x, also known as the double angle identity for cosine, is a trigonometric formula that expresses the cosine of a double angle (2x) using various trigonometric functions. It can be represented in multiple forms: cos 2x = cos² x – sin² x, cos 2x = 2 cos² x – 1, cos 2x = 1 – 2 sin² x, and cos 2x = (1 – tan² x) / (1 + tan² x). These identities are derived using the sum of angles formula and Pythagorean identities. The cos2x identity is essential for solving trigonometric equations, simplifying expressions, and analyzing periodic functions, making it a fundamental tool in mathematics and its applications in fields like physics, engineering, and computer science.

Cos2x Identity

1. In Terms of Cosine and Sine:
   • Cos 2x = cos² x – sin² x
2. In Terms of Cosine Only:
   • Cos 2x = 2 cos² x – 1
3. In Terms of Sine Only:
   • Cos 2x = 1 – 2 sin² x
4. In Terms of Tangent:
   • Cos 2x = (1 – tan² x) / (1 + tan² x)

Cos2x In Terms of sin x

1. Start with the double-angle identity:
   Cos2x = Cos²x – Sin²x
2. Use the trigonometric identity Cos²x + Sin²x = 1 to express Cos²x in terms of Sin²x:
   Cos²x = 1 – Sin²x
3. Substitute this into the double-angle formula:
   Cos2x = (1 – Sin²x) – Sin²x
4. Simplify the expression:
   Cos2x = 1 – Sin²x – Sin²x
5. Combine like terms:
   Cos2x = 1 – 2Sin²x

Hence, the formula for Cos2x in terms of Sin x is:

Cos2x = 1 – 2Sin²x

Cos2x In Terms of cos x

1. Start with the double-angle identity:
   Cos2x = Cos²x – Sin²x
2. Use the trigonometric identity Sin²x = 1 – Cos²x to express Sin²x in terms of Cos²x:
   Sin²x = 1 – Cos²x
3. Substitute this into the double-angle formula:
   Cos2x = Cos²x – (1 – Cos²x)
4. Simplify the expression:
   Cos2x = Cos²x – 1 + Cos²x
5. Combine like terms:
   Cos2x = 2Cos²x – 1

Hence, the formula for Cos2x in terms of Cos x is:

Cos2x = 2Cos²x – 1

Cos2x In Terms of tan x

1. Start with the double-angle identity:
   Cos2x = Cos²x – Sin²x
2. Use the trigonometric identities Cos²x = 1 / (1 + Tan²x) and Sin²x = Tan²x / (1 + Tan²x)²:
   Cos2x = (1 / (1 + Tan²x)) – (Tan²x / (1 + Tan²x))
3. Express both terms with a common denominator:
   Cos2x = (1 – Tan²x) / (1 + Tan²x)

Hence, the formula for Cos2x in terms of Tan x is:

Cos2x = (1 – Tan²x) / (1 + Tan²x)

Properties of Cos2x

Periodicity

Cos2x has a period of π. This means that the function repeats its values every π units. For example, Cos2(x + π) is equal to Cos2x.

Symmetry

Cos2x is an even function, meaning it is symmetric about the y-axis. This implies that Cos2(-x) is equal to Cos2x.

Range

The range of Cos2x is between -1 and 1, inclusive. In other words, Cos2x will always produce values within this interval.

Critical Points

Cos2x has critical points where its derivative is zero. These points occur at x = nπ/2 for integers n. These points correspond to the local maxima and minima of the function.

Maxima and Minima

Cos2x achieves its maximum value of 1 and its minimum value of -1 at specific points:

• Cos2x = 1 when x = nπ for integers n.
• Cos2x = -1 when x = π/2 + nπ for integers n.

Relation to Other Functions

Cos2x can be expressed in terms of other trigonometric functions:

• In terms of Cos x: Cos2x = 2Cos²x – 1
• In terms of Sin x: Cos2x = 1 – 2Sin²x
• In terms of Tan x: Cos2x = (1 – Tan²x) / (1 + Tan²x)

Derivatives and Integrals

• The derivative of Cos2x is -2Sin2x.
• The integral of Cos2x is (1/2) Sin2x + C, where C is the constant of integration.

Cos2x in relation to Other Trigonometric Functions

In Terms of Cosine (Cos x)

The double-angle formula for cosine can be expressed using only the cosine function: Cos2x = 2Cos²x – 1

In Terms of Sine (Sin x)

Cos2x can also be written in terms of the sine function: Cos2x = 1 – 2Sin²x

In Terms of Tangent (Tan x)

To express Cos2x using the tangent function, we use the identity involving tangent: Cos2x = (1 – Tan²x) / (1 + Tan²x)

In Terms of Secant (Sec x)

Though less common, Cos2x can be related to the secant function as well: Cos2x = (2 – Sec²x) / Sec²x

In Terms of Cosecant (Csc x)

Cos2x can also be expressed in terms of the cosecant function: Cos2x = (2Csc²x – 1) / Csc²x

In Terms of Cotangent (Cot x)

Finally, the double-angle formula for cosine can be written using the cotangent function: Cos2x = (Cot²x – 1) / (Cot²x + 1)

Solved Problems

Problem 1: Evaluating cos⁡2x given cos⁡x

Question: Given cos⁡x = 1/2, find cos⁡2x

Solution: Using the double-angle formula for cosine: cos⁡2x = 2cos⁡²x−1.

Substitute cos⁡x=1/2:
cos2x = 2 (1/2)² – 1 = 2 (1/4) -1 = 1/2-1 = -1/2

So, cos2x = -1/2

---

Problem 2: Evaluating cos⁡2x given sin⁡x

Question: Given sin⁡x=√3/2​​, find cos⁡2x.

Solution: First, use the Pythagorean identity to find cos⁡x: sin²x+cos⁡²x = 1.

So, (√3/2)²+cos²x=1.
This gives 3/4+cos⁡²x = 1, thus cos²x =1/4, meaning cos⁡x=±1/2​.

Using cos⁡x = 1/2 or cos⁡x=−1/2​:
cos⁡2x = 2(1/2)²−1 = 1/2−1 = −1/2.

So, cos⁡2x = −1/2​.

---

Problem 3: Solving cos⁡2x=0.5

Question: Solve for cos⁡2x = 0.5.

Solution: We know that cos⁡2x=0.5.

This corresponds to: 2x=±π3+2kπ for k∈Z.

Thus: x=±π/6+kπ.

So, the solutions are: x=π/6+kπ or x=−π/6+kπ.

---

Problem 4: Maximum and Minimum Values of cos⁡2x

Question: What are the maximum and minimum values of cos⁡2x?

Solution: The cosine function oscillates between -1 and 1. Since cos⁡2x is just a cosine function with a different argument, it also oscillates between -1 and 1.

Therefore:
Maximum value of cos⁡2x is 1.
Minimum value of cos⁡2x is -1.

---

Problem 5: Expressing cos⁡2x in terms of tan⁡x

Question: Express cos⁡2x in terms of tan⁡x

Solution: Using the identity cos⁡2x=1−tan⁡²x/1+tan⁡²x​:

We start from the double-angle identity: cos⁡2x = 2cos⁡²x−1.

Using cos⁡²x=1/1+tan²x​:
cos⁡2x = 2(1/1+tan⁡²x)−1 = 2/(1+tan⁡²x)−1 = 2−(1+tan²x)/(1+tan⁡²x) = (1−tan⁡²x)/(1+tan²x).

So, cos⁡2x=1−tan⁡²x/1+tan⁡²x.

---