Square & Square Root of 3721

Within the realm of algebraic mathematics, squares and square roots play a pivotal role. Squaring a number, such as 3721, involves multiplying it by itself, yielding 13,841. This basic operation is crucial for delving into rational and irrational numbers. A firm grasp of these foundational concepts enriches comprehension of mathematical relationships and patterns. Squares unveil inherent number properties, while square roots unravel complex numerical mysteries. These ideas act as guiding lights, directing mathematical explorations into fractional realms. Mastery of squares and square roots empowers mathematicians to traverse diverse mathematical landscapes, revealing the elegance and intricacy inherent within algebraic frameworks.

Square of 3721

3721² (3721 × 3721) = 13,841

The square of 3721 equals 13,841, attained by multiplying 3721 by itself, a fundamental operation in algebraic mathematics, revealing inherent number properties.

Square Root of 3721

√3721 = 61

The square root of 3721 is 61. This fundamental mathematical operation discloses the value that, when multiplied by itself, equals 3721.

Square Root of 3721: 61

Exponential Form: 3721^½ or 3721^0.5

Radical Form: √3721

Is the Square Root of 3721 Rational or Irrational?

The square root of 3721 is rational.

Rational numbers are expressible as the quotient of two integers. In contrast, irrational numbers cannot be represented as fractions of integers. Examples of irrational numbers include the square roots of non-perfect squares.

Methods to Find the Value of the Root 3721

• Prime Factorization Method: Break down 3721 into its prime factors. However, since 3721 is a perfect square (61 × 61), its prime factorization is straightforward.
• Using a Calculator: Most calculators feature a square root function, facilitating direct calculation of the square root of 3721.
• Estimation: Recognizing that 3721 is a perfect square, its square root is precisely 61.

Square Root of 3721 by Long Division Method

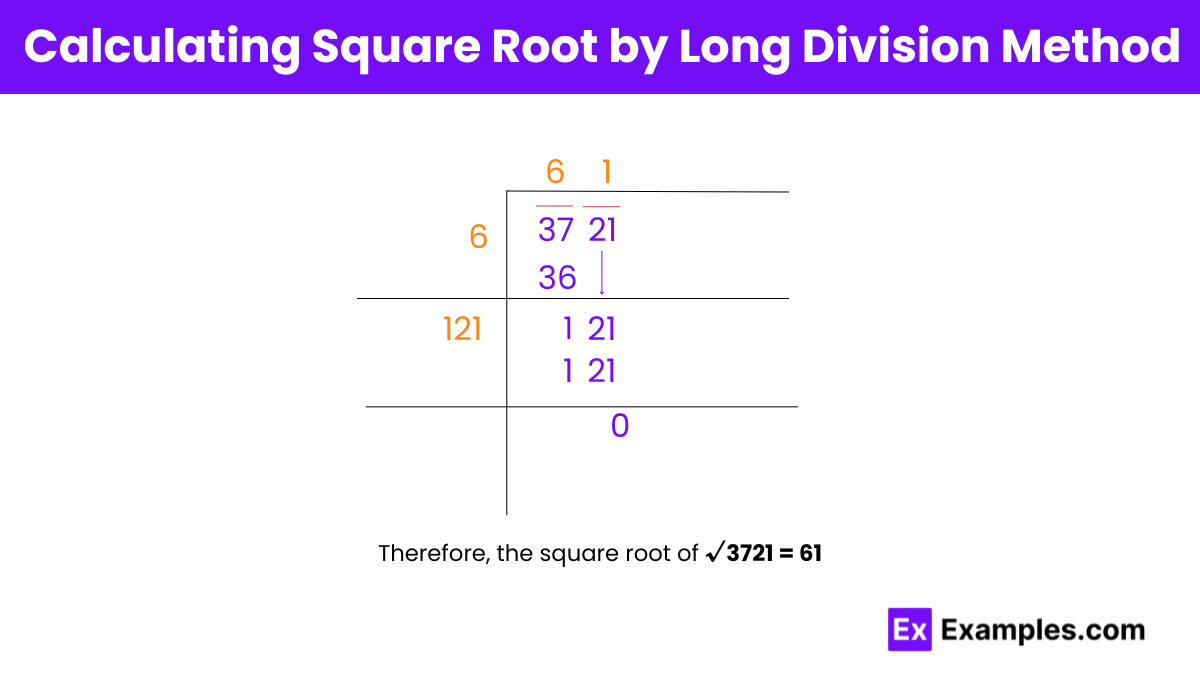
Step 1: Forming pairs

Initial number: 37 21

Step 2: Find a number Y such that Y² ≤ 37:

Let’s choose Y as 6 since 6² = 36, which is less than or equal to 37.

Step 3: Divide 37 by 6 with quotient as 6:

37 ÷ 6 = 6 with a remainder of 1.

Step 4: Bring down the next pair (21) to the right of the remainder (1):

The new dividend is now 121.

Step 5: Add the last digit of the quotient (6) to the divisor (6) to get 12:

Now, we have 12 as the divisor.

Step 6: To the right of 12, find a digit Z such that 12Z × Z ≤ 121

Let’s choose Z as 1, so we have 121 × 1 = 121, which is less than or equal to 121.

Step 7: After finding Z, together 12 and Z (1) form a new divisor 121 for the new dividend 121.

The new dividend is now 0.

Step 8: Divide 121 by 121 with the quotient as 1

121 ÷ 121 = 1 with a remainder of 0.

Is 3721 a Perfect Square or Not?

Yes, 3721 is a perfect square.

A perfect square can be expressed as the square of an integer. Therefore, the square root of 3721 is a rational number.