Cosine

What is Cosine?

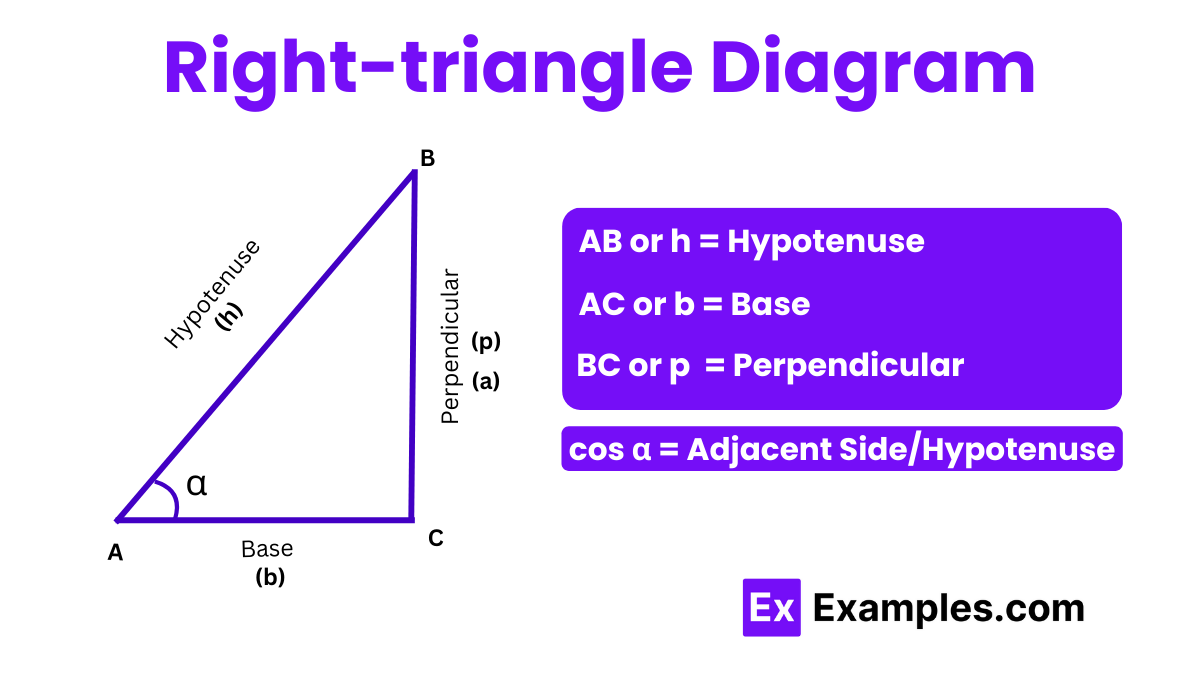
In mathematics, “cosine” is a trigonometric function that describes the relationship between the angles and sides of a right-angled triangle. It is one of the basic functions in trigonometry, alongside sine and tangent. The cosine of an angle in a right-angled triangle is defined as the ratio of the length of the adjacent side to the length of the hypotenuse.

Cosine Formula

From the definition of cosine in trigonometry, it is known that cosine of an angle in a right-angled triangle is the ratio of the length of the adjacent side to the length of the hypotenuse. Thus, for angle α .

cos α = AC/AB

Or,

cos α = b/h

where ( b ) is the length of the side adjacent to angle ( α ), and ( h ) is the hypotenuse of the triangle.

Download This Image

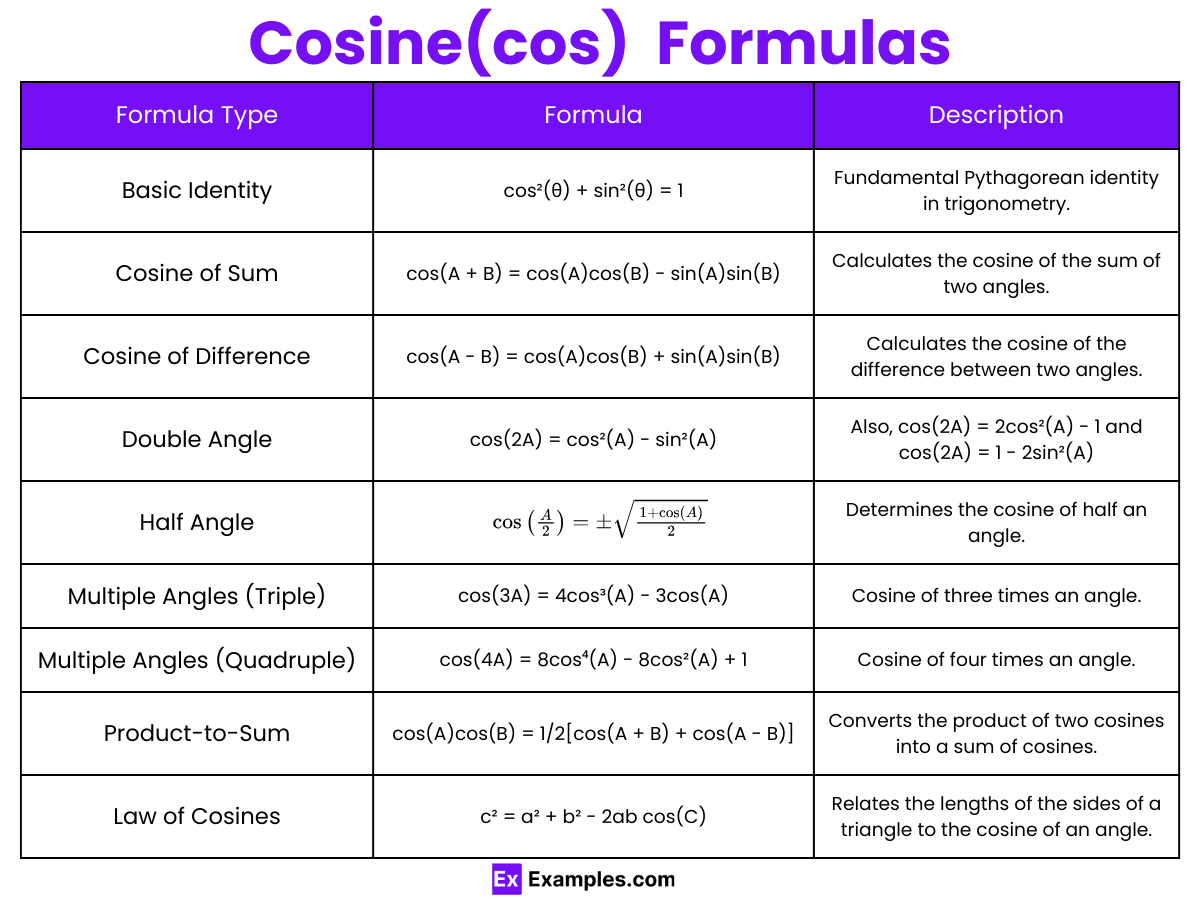
Trigonometric Identities Involving Cosine

Basic Identity: The square of cosine added to the square of sine equals one: cos²(θ) + sin²(θ) = 1

Cosine of Sum and Difference: The cosine of the sum of two angles is given by: cos(A + B) = cos(A) cos(B) – sin(A) sin(B)

The cosine of the difference of two angles is: cos(A – B) = cos(A) cos(B) + sin(A) sin(B)

Double Angle Formulas: The double angle formula for cosine is expressed in several ways: cos(2A) = cos²(A) – sin²(A)

Alternatively: cos(2A) = 2cos²(A) – 1 Or: cos(2A) = 1 – 2sin²(A)

Half Angle Formulas: The half-angle formula for cosine is:

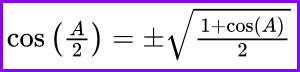
Cosine of Multiple Angles: For three times an angle, it is: cos(3A) = 4cos³(A) – 3cos(A)

For four times an angle: cos(4A) = 8cos⁴(A) – 8cos²(A) + 1

Product-to-Sum Formulas: The product of two cosines can be expressed as a sum: cos(A) cos(B) = 1/2[cos(A + B) + cos(A – B)]

Law of Cosines: Useful for finding a side or angle in any triangle: c² = a² + b² – 2ab cos(C) where c is the side opposite the angle C, and a and b are the other two sides.

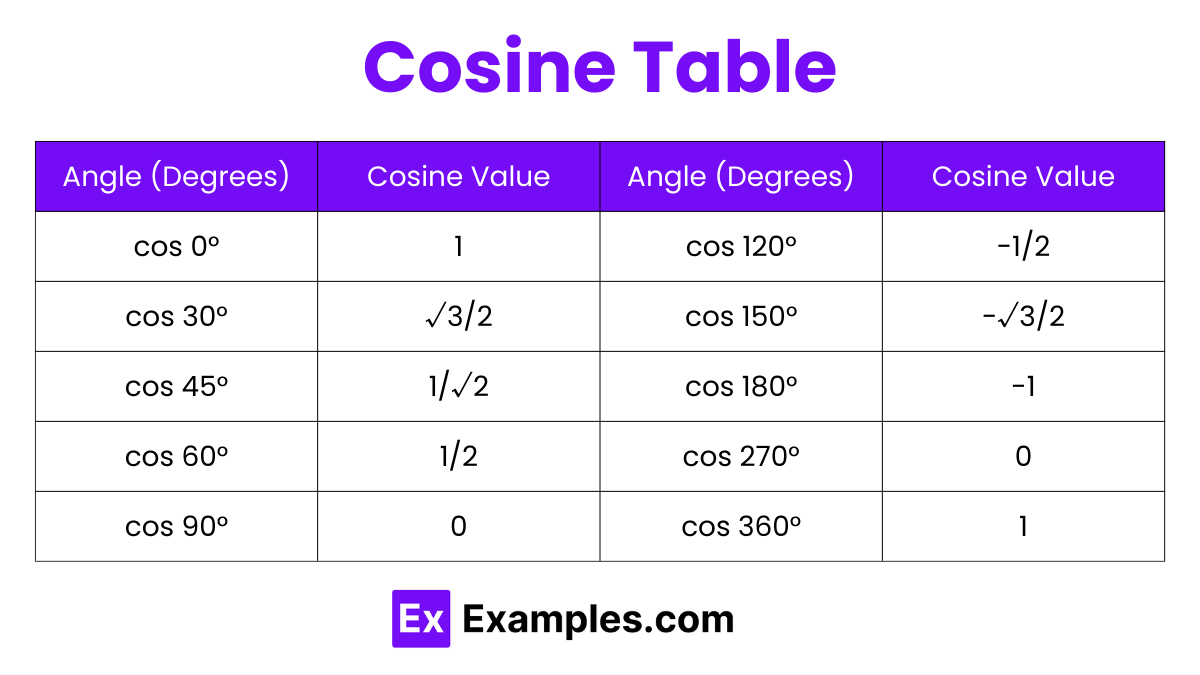
Cosine Table

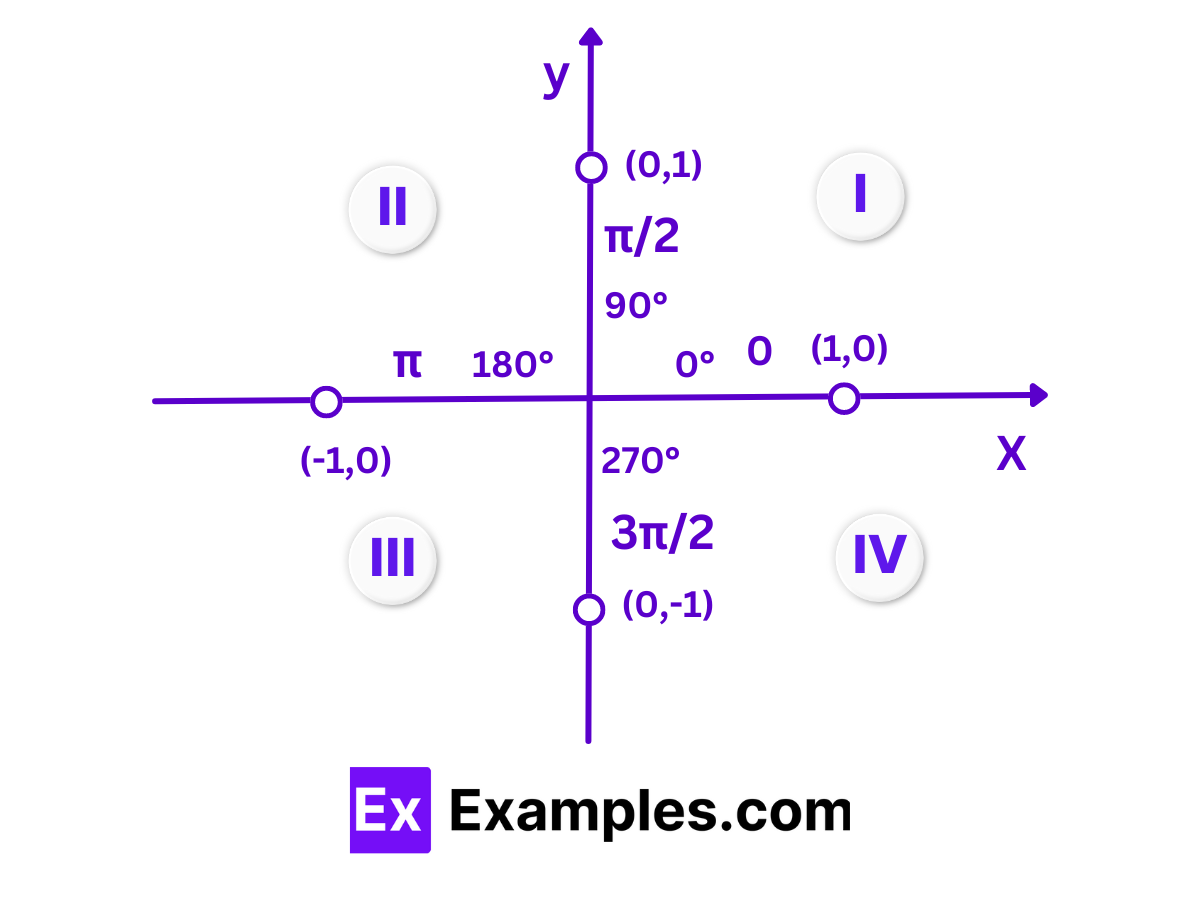
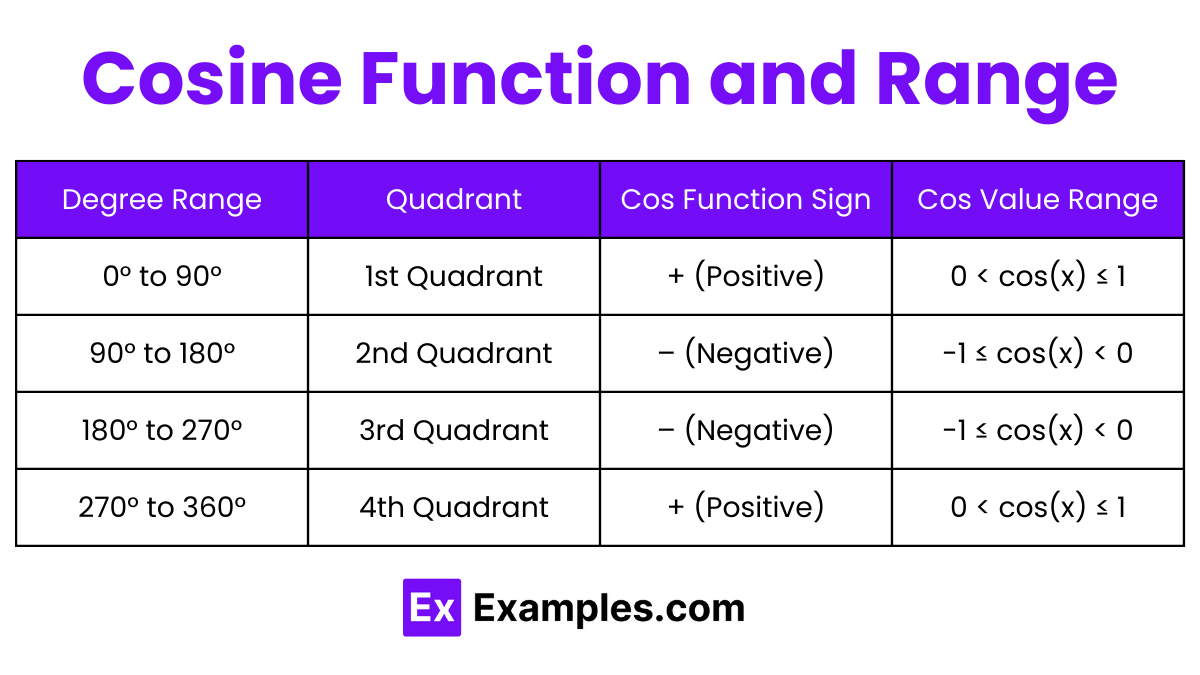
Cosine Properties With Respect to the Quadrants

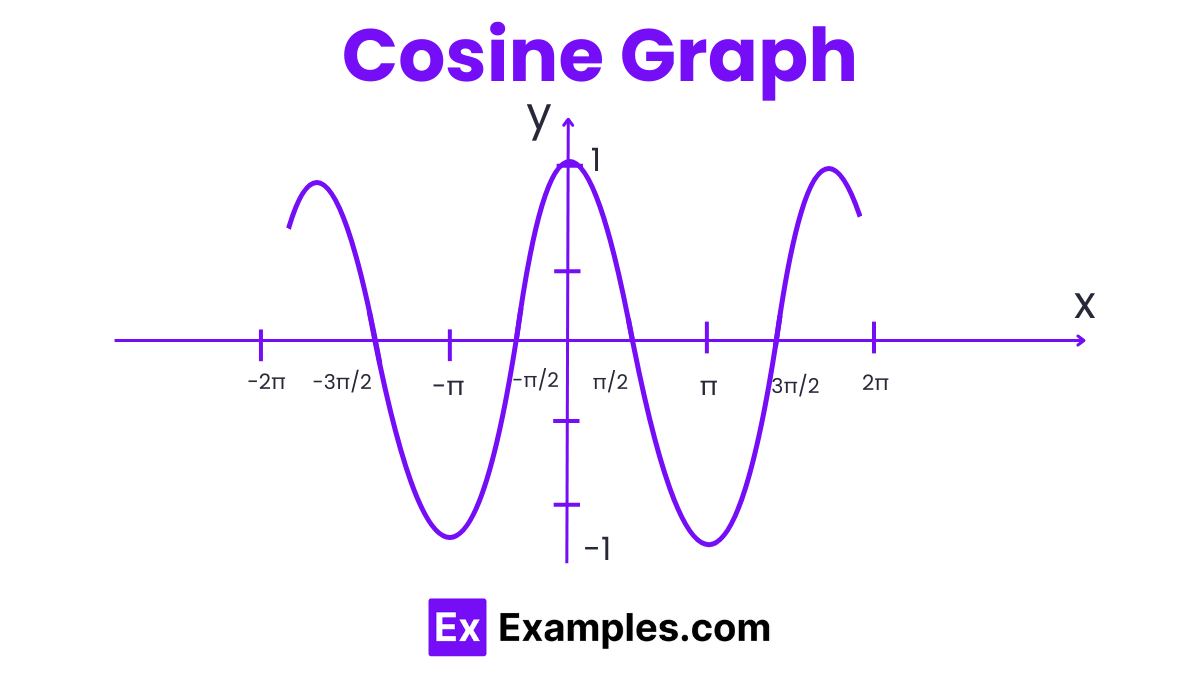
Cosine Graph

The cosine graph, similar to the sine graph, exhibits an oscillating pattern, but with a distinct phase shift. While the sine graph initiates at zero, the cosine graph starts at its maximum value of 1. This occurs because the cosine function represents the horizontal coordinate of a point on the unit circle, beginning at the topmost point (1,0). As the angle increases from 0 to 360 degrees (or from 0 to 2π ), the cosine value decreases to -1 and then returns to 1, completing a full cycle. This waveform reflects the cosine function’s characteristic shape, moving from its peak, descending to its lowest value, and ascending back to the peak as the angle progresses through 360 degrees.

Arccos (Inverse Cosine)

The inverse cosine function, denoted as cos⁻¹ or arccos, is used to determine the angle in a right-angled triangle when the ratio of the length of the adjacent side to the hypotenuse is known. This function provides the angle whose cosine is the given ratio, thereby facilitating the measurement of angles in trigonometric applications.

For a right triangle with sides 1, 2, and √3, the cos function can be used to measure the angle.

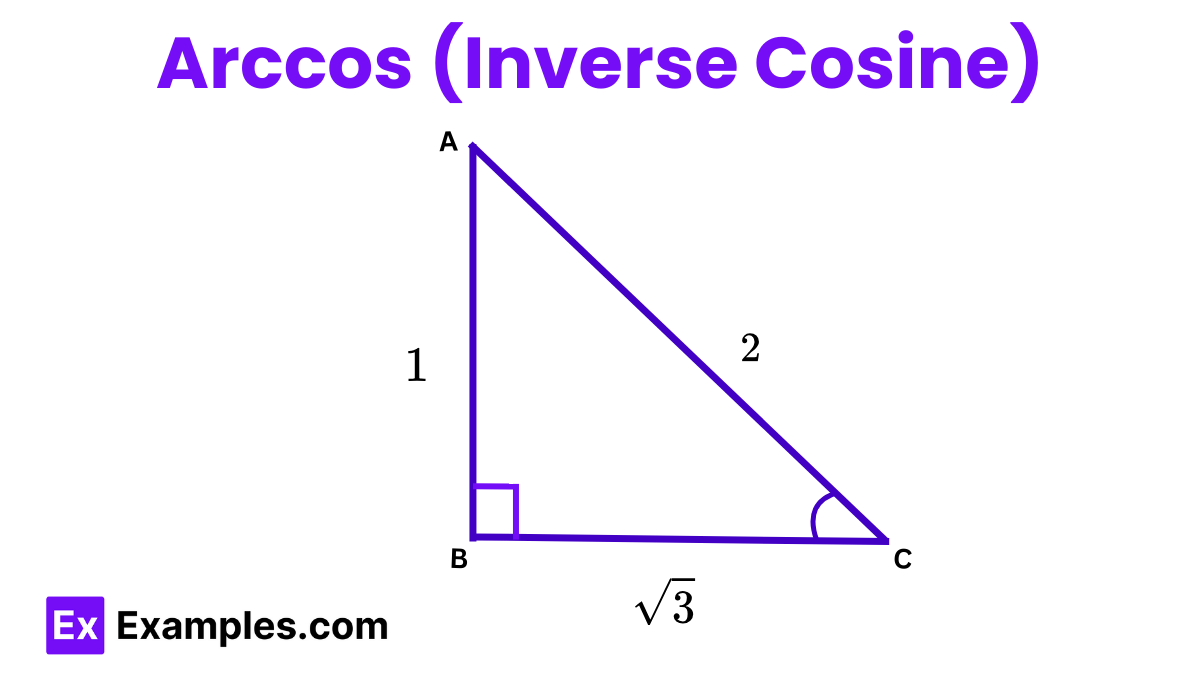
In this, the cos of angle A will be, cos(a)= adjacent/hypotenuse.So, cos(a) = √3/2Now, the angle “a” will be cos−1(√3/2)

Or, a = π/6 = 30°

Cos Calculus

For cosine function f(x) = cos(x), the derivative and the integral will be given as:

• Derivative of cos(x), f′ (x) = −sin (x)
• Integral of cos(x), ∫f (x) dx = sin(x) + C)      [where C is the constant of integration)

Law of Cosines in Trigonometry

he Law of Cosines is a fundamental theorem in trigonometry that generalizes the Pythagorean theorem. It provides a formula to calculate the length of any side of a triangle when the lengths of the other two sides and the measure of the included angle are known. This law is particularly useful in solving triangles that are not right-angled.

According to cos law, the side “c” will be:

c² = a² + b² − 2ab cos (C)

(This equation helps determine the third side of a triangle when two sides and the included angle are given. It can also be used to find the angles of a triangle if all three sides are known. This makes the Law of Cosines extremely valuable for fields requiring precise measurements and calculations, such as engineering, navigation, and physics.)

What is the Cosine Formula?

The cosine of an angle (theta) in a right-angled triangle is given by:
[ Cos(theta) = (Adjacent Side) / (Hypotenuse) ]

How do you calculate the Cosine of an angle?

To calculate the cosine of an angle:

1. Identify the lengths of the adjacent side and the hypotenuse of the right-angled triangle.
2. Use the formula Cos(theta) = (Adjacent Side) / (Hypotenuse).

For example, if the adjacent side is 3 units and the hypotenuse is 5 units:
[ Cos(theta) = 3 / 5 = 0.6 ]

What is the Cosine of 0, 30, 45, 60, and 90 degrees?

The cosine values for common angles are:

• Cos(0 degrees) = 1
• Cos(30 degrees) = √3/2 ≈ 0.866
• Cos(45 degrees) = 1/√2 ≈ 0.707
• Cos(60 degrees) = 1/2 = 0.5
• Cos(90 degrees) = 0

What are the properties of the Cosine function?

• Range: The cosine function ranges from -1 to 1.
• Periodicity: The function is periodic with a period of 2π. This means Cos(theta + 2π) = Cos(theta).
• Even Function: Cosine is an even function, meaning Cos(-theta) = Cos(theta).

How is Cosine used in real life?

Cosine is used in various applications including:

• Engineering: Calculating forces and angles in structures.
• Physics: Analyzing wave patterns and oscillations.
• Computer Graphics: Rendering shapes and rotations.
• Navigation: Determining the shortest path between two points on the globe using spherical trigonometry.

How is Cosine related to the Unit Circle?

In the unit circle, the cosine of an angle (theta) is the x-coordinate of the point where the terminal side of the angle intersects the circle. The unit circle helps visualize and understand the properties of the cosine function, such as its periodicity and symmetry.

What is the difference between Cosine and Sine?

Cosine and sine are both trigonometric functions, but they differ in how they relate the sides of a right triangle to an angle:

• Cosine: Cos(theta) = (Adjacent Side) / (Hypotenuse)
• Sine: Sin(theta) = (Opposite Side) / (Hypotenuse)

How can Cosine be used to find an angle?

To find an angle given the cosine value, use the inverse cosine function, denoted as Cos^-1 or arccos. For example, if Cos(theta) = 0.5:
[ Theta = Cos^-1(0.5) = 60 degrees ]

What is the Cosine Law?

The Cosine Law, also known as the Law of Cosines, relates the sides of any triangle to the cosine of one of its angles. It is given by:
[ c^2 = a^2 + b^2 – 2ab * Cos(C) ]
where a, b, and c are the sides of the triangle, and C is the angle opposite side c.

Practice Qustions

What is the Cosine Formula?

The cosine of an angle (theta) in a right-angled triangle is given by:
[ Cos(θ) = (Adjacent Side) / (Hypotenuse) ]

How do you calculate the Cosine of an angle?

To calculate the cosine of an angle:

1. Identify the lengths of the adjacent side and the hypotenuse of the right-angled triangle.
2. Use the formula Cos(θ) = (Adjacent Side) / (Hypotenuse).

For example, if the adjacent side is 3 units and the hypotenuse is 5 units:
[ Cos(theta) = 3 / 5 = 0.6 ]

What is the Cosine of 0, 30, 45, 60, and 90 degrees?

The cosine values for common angles are:

• Cos(0 degrees) = 1
• Cos(30 degrees) = √3/2 ≈ 0.866
• Cos(45 degrees) = 1/√2 ≈ 0.707
• Cos(60 degrees) = 1/2 = 0.5
• Cos(90 degrees) = 0

What are the properties of the Cosine function?

• Range: The cosine function ranges from -1 to 1.
• Periodicity: The function is periodic with a period of 2π. This means Cos(θ + 2π) = Cos(θ).
• Even Function: Cosine is an even function, meaning Cos(-θ) = Cos(θ).

How is Cosine used in real life?

Cosine is used in various applications including:

• Engineering: Calculating forces and angles in structures.
• Physics: Analyzing wave patterns and oscillations.
• Computer Graphics: Rendering shapes and rotations.
• Navigation: Determining the shortest path between two points on the globe using spherical trigonometry.

How is Cosine related to the Unit Circle?

In the unit circle, the cosine of an angle (theta) is the x-coordinate of the point where the terminal side of the angle intersects the circle. The unit circle helps visualize and understand the properties of the cosine function, such as its periodicity and symmetry.

What is the difference between Cosine and Sine?

Cosine and sine are both trigonometric functions, but they differ in how they relate the sides of a right triangle to an angle:

• Cosine: Cos(theta) = (Adjacent Side) / (Hypotenuse)
• Sine: Sin(theta) = (Opposite Side) / (Hypotenuse)

How can Cosine be used to find an angle?

To find an angle given the cosine value, use the inverse cosine function, denoted as Cos^-1 or arccos. For example, if Cos(theta) = 0.5:
[ Theta = Cos^-1(0.5) = 60 degrees ]

FAQs