Bernoulli’s Principle – Examples, Definition, Derivation, Applications

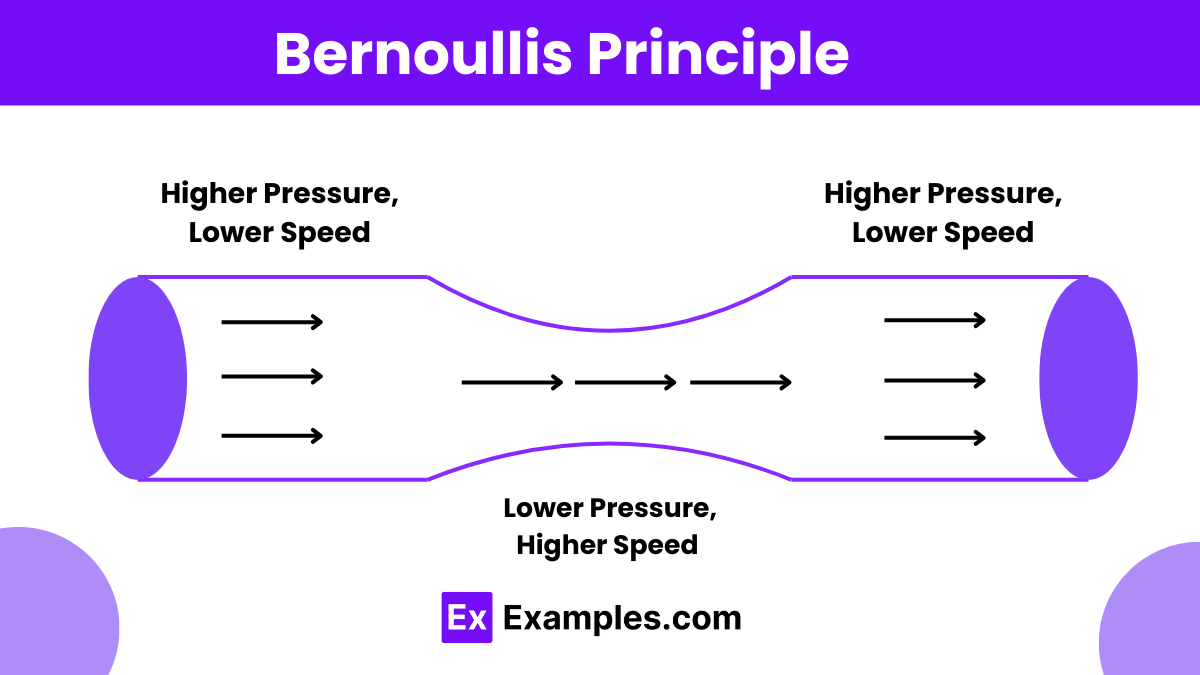
Bernoulli’s Principle is a foundational concept in fluid dynamics, derived from the conservation laws of mechanics, specifically the conservation of energy. It states that in a flowing fluid, an increase in the fluid’s speed occurs simultaneously with a decrease in pressure or potential energy. This principle is crucial for understanding various phenomena in physics and engineering, such as the lift generated by airplane wings or the behavior of gases in pipelines. By applying the laws of motion and energy conservation, Bernoulli’s Principle helps explain how and why fluids behave as they do under different conditions. This relationship between speed, pressure, and potential energy is instrumental in many applications across both natural and technological systems.

What is Bernoullis Principle?

Bernoullis Principle Formula

The formula that represents Bernoulli’s Principle is expressed as follows:

Here’s what each term represents:

• 𝑃 is the static pressure within the fluid.
• 𝜌 is the density of the fluid.
• 𝑣 is the velocity of the fluid at a point.
• 𝑔 is the acceleration due to gravity.
• ℎ is the height above a reference level, representing the potential energy due to the fluid’s elevation.

This equation essentially states that the sum of the static pressure, dynamic pressure (1/2𝜌𝑣²), and hydrostatic pressure (𝜌𝑔ℎ) is constant along any streamline in a steady, incompressible flow with negligible viscosity. This relationship allows for predictions of changes in fluid velocity, pressure, and elevation.

Examples of Bernoullis Principle Formula

• Aircraft Wings: In aviation, the shape of an airplane wing (airfoil) is designed so that air flows faster over the top of the wing than underneath. According to Bernoulli’s Principle, the increase in velocity atop the wing leads to a decrease in pressure. This pressure difference between the upper and lower surfaces of the wing generates lift, allowing the airplane to ascend.
• Venturi Meter: This device is used to measure the flow rate of a fluid through a pipe. A Venturi meter has a constricted section (throat) where the fluid velocity increases, causing a drop in pressure according to Bernoulli’s equation. By measuring the pressure difference between the wider part of the pipe and the throat, the flow rate can be determined.
• Atomizers: These devices use Bernoulli’s Principle to disperse liquids into a fine spray. When air passes over a narrow passage at high speed, it reduces the pressure at that point, sucking the liquid up through a tube and dispersing it as a mist.
• Spinning Balls in Sports: When a ball (like a soccer ball, tennis ball, or baseball) is spun through the air, it experiences different air speeds along its surface. Faster airflow on one side compared to slower airflow on the other creates a pressure difference, causing the ball to curve in flight—a phenomenon often referred to as the “Magnus effect” but closely related to Bernoulli’s principle.
• Hydraulic Jump: When a fast-moving layer of water in a channel (like a river or a spillway) encounters a region where the flow slows down, the sudden change in velocity leads to a rapid increase in the water surface level, forming a “jump”. The faster flow has lower pressure, and when it slows down, the pressure increases, pushing the water upwards.

Derivation of Bernoullis Principle

Step 1: Conservation of Energy

Bernoulli’s Principle is essentially an application of the conservation of mechanical energy to fluid flow. The total mechanical energy for a fluid element includes kinetic energy, potential energy due to gravity, and energy related to pressure.

Step 2: Fluid Dynamics and Infinitesimal Control Volume

Consider a small element of fluid moving along a streamline. The forces acting on this fluid element are due to pressure and gravity.

Step 3: Kinetic Energy, Potential Energy, and Pressure Work

• Kinetic Energy: The kinetic energy per unit volume of the fluid is 1/2𝜌𝑣​², where 𝜌ρ is the fluid density and 𝑣v is the flow velocity.
• Potential Energy: The potential energy per unit volume due to elevation ℎ is 𝜌𝑔ℎ.
• Pressure Work: As fluid moves from one section to another, work is done against the fluid pressure. For a fluid moving from an area 𝐴₁ with pressure 𝑃₁​ to area 𝐴₂​ with pressure 𝑃₂, the work done by the pressure is represented by the pressure-volume work term 𝑃𝑑𝑉, where 𝑉 is the volume of the fluid element.

Step 4: Applying the Work-Energy Theorem

Assuming no heat transfer or energy losses (ideal conditions), the total mechanical energy remains constant along a streamline:

d(1/2​ρv²)+d(ρgh)+PdV = 0

Here, 𝑑d represents the differential changes.

Step 5: Incorporating the Continuity Equation

For incompressible flow, the Continuity Equation 𝜌𝐴𝑣=constantρAv=constant implies constant mass flow rate, helping relate velocity and cross-sectional area changes.

Step 6: Differential Form and Integration

Converting the work-energy balance into a form using differentials and simplifying using the properties of incompressible flow:

dP​/p+vdv+gdh = 0

Integrating this equation along a streamline from points 1 to 2, assuming steady flow and constant density 𝜌ρ, gives Bernoulli’s equation:

P₁​+1​/2ρv​²₁+ρgh₁ ​= P₂​+1​/2ρv​²₂​+ρgh₂​ = constant

This equation, Bernoulli’s equation, shows that the sum of pressure energy, kinetic energy, and potential energy per unit volume remains constant along a streamline in a steady, incompressible, non-viscous flow. It illustrates how changes in velocity and elevation affect the fluid pressure within a flow field.

Applications of Bernoullis Principle

• Aerodynamics and Flight: Perhaps the most famous application of Bernoulli’s Principle is in explaining how airplane wings generate lift. The shape of an airplane wing is designed so that air flows faster over the top of the wing and slower underneath. According to Bernoulli’s Principle, the pressure on the top of the wing where the air velocity is higher will be lower than the pressure on the bottom of the wing. This pressure difference creates lift, allowing the airplane to ascend.
• Venturi Effect: This effect is observed in a Venturi tube, where a fluid flows through a constricted section. According to Bernoulli’s Principle, the velocity of the fluid increases and the pressure decreases as the fluid passes through the constriction. This principle is used in various devices such as carburetors and aspirators, where it helps in mixing fluids or drawing fluids into a stream.
• Hydrodynamics: Bernoulli’s Principle is applied in the study and design of water flow in pipes, channels, and open bodies of water. It helps in designing water pumps and hydroelectric power plants, where understanding the relationship between pressure, velocity, and elevation is crucial.
• Meteorology: In meteorology, Bernoulli’s Principle helps explain wind patterns and weather phenomena. For example, when wind speed increases as it passes over mountains or through valleys, pressure variations can lead to the formation of different weather patterns.
• Medical Applications: In medicine, Bernoulli’s Principle is used in devices like the Venturi mask, which is used to deliver precise concentrations of oxygen to patients through controlled air flows. It also helps in understanding the flow of blood in arteries and veins, assisting in the diagnosis and treatment of cardiovascular diseases.
• Sports: In sports, Bernoulli’s Principle helps explain the behavior of balls in sports like tennis, golf, and soccer when spin is applied. The spinning ball creates different velocities on either side, leading to pressure differences that result in curved trajectories, known as the “Magnus effect.”

FAQs

What are common misconceptions about Bernoulli’s Principle?

A common misconception is that Bernoulli’s Principle is the sole explanation for lift in aircraft wings. While it plays a significant role, lift is also influenced by Newton’s Third Law as the wing deflects air downward. Another misconception is that the principle applies universally to all fluid motions, ignoring effects like viscosity and compressibility.

What is the Venturi effect and how is it related to Bernoulli’s Principle?

The Venturi effect describes the reduction in fluid pressure that results when a fluid flows through a constricted section of a pipe. According to Bernoulli’s Principle

How does Bernoulli’s Principle impact everyday life?

Bernoulli’s Principle has practical implications in everyday life, including the design of exhaust and ventilation systems, the operation of garden sprayers, and the engineering of dams and water conduits.