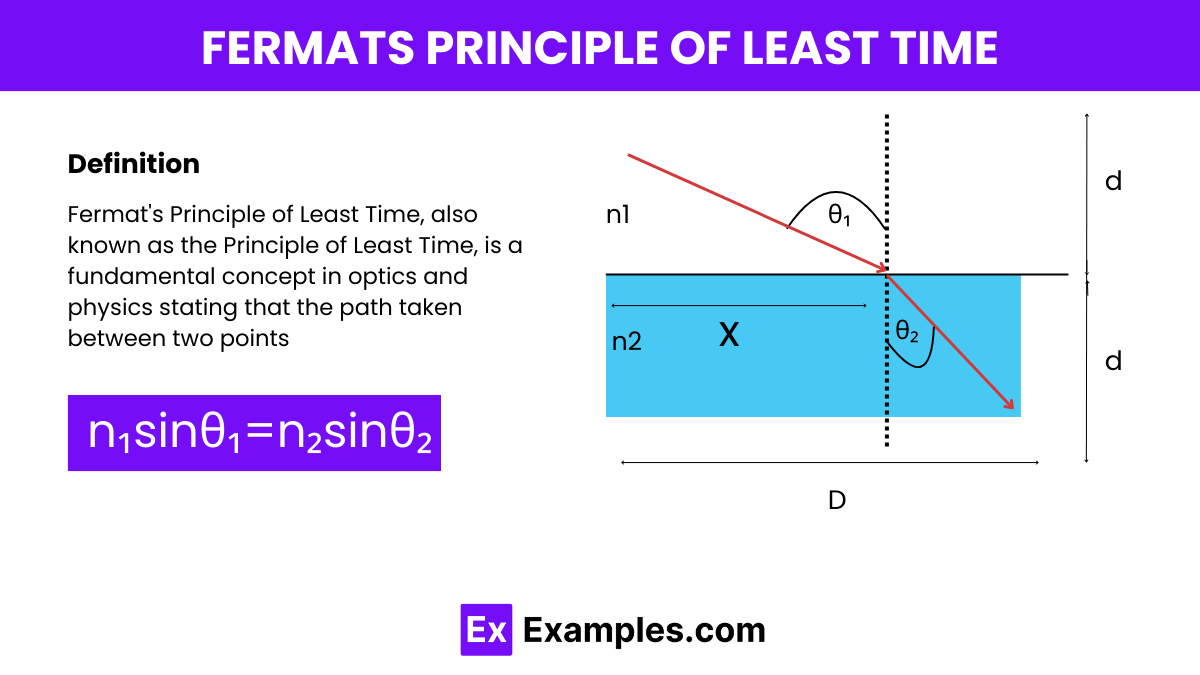
What does Fermat's Principle of Least Time state about the path taken by light?
Light takes the path that covers the shortest distance.
Light takes the path that requires the least time to travel.
Light takes the path with the least obstacles.
Light takes the path with the highest speed.