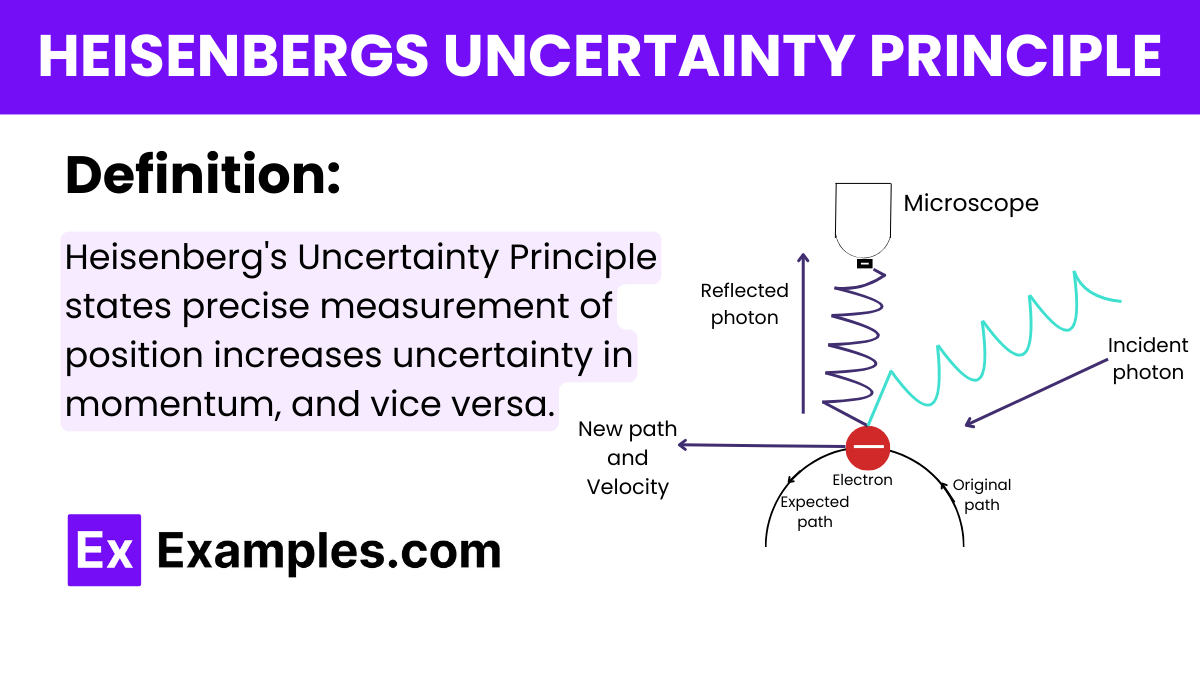
What does Heisenberg\'s Uncertainty Principle state about the simultaneous measurement of position and momentum?
Both can be precisely measured
Only position can be measured precisely
Both cannot be precisely measured
Only momentum can be measured precisely