Friedmann Equations

The Friedmann Equations, fundamental in the laws of cosmology and astrophysics, form the core of modern cosmological models. They describe how the universe expands or contracts over time based on the principles of general relativity. These equations ingeniously link the density of matter and energy in the universe to the rate of expansion, offering a mathematical framework that underpins much of physical cosmology. Thus, they provide critical insights into the dynamics of the universe, aligning with the overarching laws of physics.

What Is Friedmann Equations?

The Friedmann Equations, derived from Albert Einstein’s theory of general relativity, serve as the foundation for understanding how the universe evolves over time. Essentially, they describe the expansion or contraction of the universe by relating the rate of change in the universe’s scale factor to the density of matter and energy it contains. Consequently, these equations allow cosmologists to predict the past and future dynamics of the universe under different scenarios, firmly anchoring them within the framework of cosmological physics.

Friedmann Equations Formula

The Friedmann Equations are expressed as follows:

First Friedmann Equation:

(𝑎˙/𝑎)²=8𝜋𝐺/3𝜌+Λ/3−𝑘/𝑎²

where:

• a˙ is the time derivative of the scale factor 𝑎,
• G is the gravitational constant,
• ρ is the energy density of the universe,
• Λ is the cosmological constant,
• k is the curvature of space (0 for flat, +1 for closed, -1 for open),
• a is the scale factor.

Second Friedmann Equation:

𝑎¨/𝑎=−4𝜋𝐺/3(𝜌+3𝑝)+Λ/3

where:

• 𝑎¨ is the second time derivative of the scale factor,
• p is the pressure of the universe.

These equations govern the expansion and dynamics of the universe, allowing cosmologists to model its evolution based on different values of density, pressure, and the cosmological constant.

Friedmann Equations Derivation

Step 1: Consider the Universe’s Symmetry

The derivation begins by considering the large-scale structure of the universe, which appears homogeneous (the same at every point) and isotropic (the same in every direction) when viewed on a large scale. This assumption simplifies the general relativity equations significantly because it allows the use of a metric that reflects this symmetry.

Step 2: Apply General Relativity to Cosmology

Einstein’s field equations are the cornerstone of general relativity, linking the geometry of spacetime (expressed through the Einstein tensor) to the energy and momentum within that spacetime (expressed through the stress-energy tensor). In the context of cosmology, these tensors are greatly simplified due to the assumed uniformity of the universe’s contents (like matter, radiation, and dark energy).

Step 3: Use the Robertson-Walker Metric

To make the equations tractable, cosmologists use the Robertson-Walker metric, which incorporates the scale factor—a function that represents how distances in the universe expand or contract over time. This metric helps relate the rate of expansion of the universe to the energy content of the universe.

Step 4: Integrate the Scale Factor

The scale factor’s role is crucial because it helps determine how the volume of the universe changes with time. The rate at which this scale factor changes (its first and second time derivatives) describes how quickly the universe is expanding or contracting, which are the central themes of the Friedmann Equations.

Step 5: Consider Different Forms of Energy

The total energy content of the universe includes matter, radiation, and dark energy, each contributing differently to the overall dynamics. These forms of energy affect the expansion rate differently, which is reflected in the Friedmann Equations. Matter and radiation tend to slow down the expansion due to their gravitational effects, while dark energy, characterized by a negative pressure, accelerates it.

Uses of Friedmann Equations

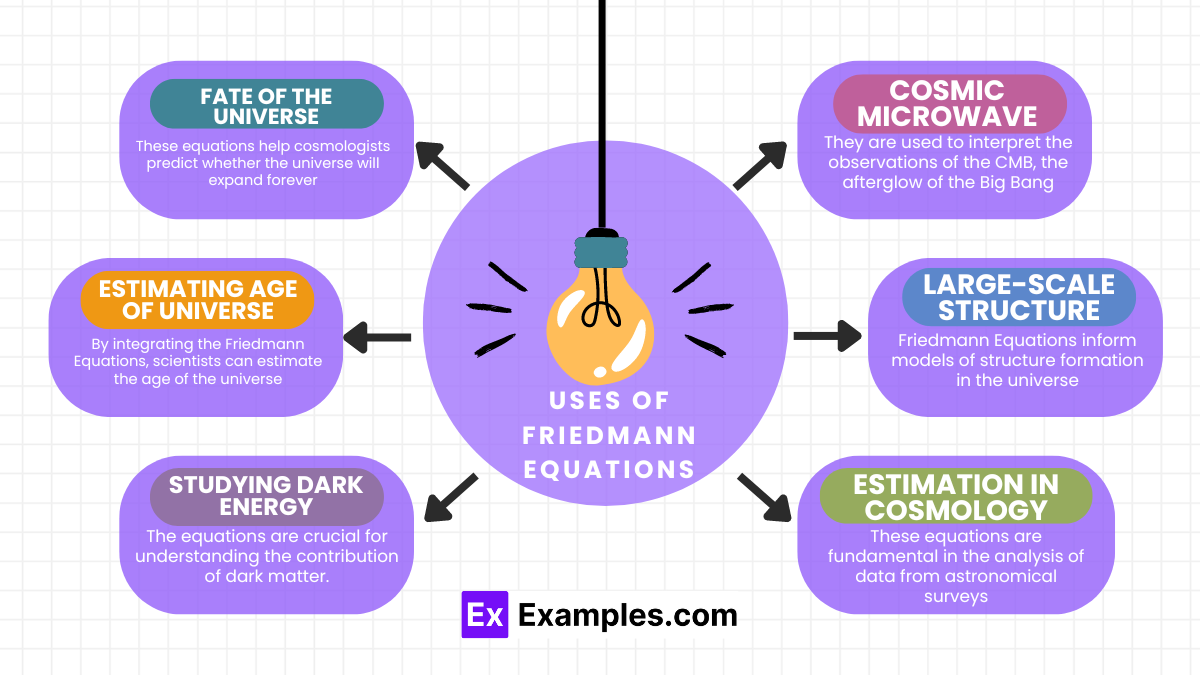
The Friedmann Equations have a wide range of applications in cosmology and astrophysics, enabling deep insights into the structure and evolution of the universe:

• Determining the Fate of the Universe: These equations help cosmologists predict whether the universe will expand forever, halt, or eventually collapse, based on its density and energy components.
• Estimating the Age of the Universe: By integrating the Friedmann Equations, scientists can estimate the age of the universe from its current rate of expansion and composition.
• Studying Dark Energy and Dark Matter: The equations are crucial for understanding the contribution of dark matter and dark energy to the overall dynamics of the universe.
• Cosmic Microwave Background (CMB) Analysis: They are used to interpret the observations of the CMB, the afterglow of the Big Bang, providing evidence for the Big Bang model of cosmology.
• Understanding the Large-scale Structure of the Universe: Friedmann Equations inform models of structure formation in the universe, explaining how galaxies and clusters of galaxies form and evolve over time.
• Parameter Estimation in Cosmology: These equations are fundamental in the analysis of data from astronomical surveys, helping to determine cosmological parameters such as the Hubble constant, matter density, and curvature of the universe.

Examples for Friedmann Equations

The Friedmann Equations are pivotal in cosmology for exploring and explaining the dynamics of the universe. Here are some specific examples of how these equations are applied:

• Cosmic Expansion: The Friedmann Equations model the expansion rate of the universe, which allows cosmologists to predict and understand how the universe has expanded from the Big Bang to its current state. These equations provide a framework to describe how the scale factor changes over time, influencing our understanding of cosmic history.
• Estimating the Age of the Universe: By using the Friedmann Equations, astronomers can estimate the age of the universe based on the current rate of expansion and the density of matter and energy. This calculation involves integrating the first Friedmann equation to determine how long it has taken for the universe to reach its current size.
• Dark Energy and the Fate of the Universe: The Friedmann Equations are used to study the effects of dark energy on the expansion of the universe. By including the cosmological constant in these equations, scientists can explore scenarios of how the universe might evolve, whether it will continue to expand indefinitely, slow down, or recollapse.
• Matter and Radiation Density: These equations help determine the relative contributions of matter, radiation, and dark energy to the total energy density of the universe. By understanding these proportions, cosmologists can describe transitions such as the radiation-dominated to matter-dominated eras and predict future transitions.
• Formation of Structures in the Universe: The Friedmann Equations are essential for modeling the gravitational dynamics that lead to the formation of large-scale structures in the universe, such as galaxies and clusters of galaxies. These calculations help explain the observed distribution of galaxies and the large-scale structure of the cosmos.

FAQ’S

What does the Friedmann equation tell us?

The Friedmann equation describes the universe’s expansion rate, linking it to its matter, radiation, and dark energy content under the framework of general relativity.

What is the Friedmann model of the cosmology?

The Friedmann model is a cosmological model derived from general relativity that predicts a dynamic, expanding or contracting universe based on its density and energy components.

What is the Friedmann equation for general relativity?

In general relativity, the Friedmann equation quantifies how the scale factor of the universe evolves over time, influenced by gravitational forces from matter and energy densities.