Navier-Stokes Equations

The Navier-Stokes Equations, foundational in the laws of fluid dynamics, describe how the velocity field of fluid substances behaves under various forces. These equations integrate principles of physics to model the motion of fluids, accounting for viscosity, pressure, and external forces like gravity. Consequently, they are essential for predicting weather patterns, designing aircraft, and understanding ocean currents, providing a comprehensive mathematical framework for analyzing fluid flow in both natural and engineered systems.

What are Navier-Stokes Equations?

SSThe Navier-Stokes Equations model the motion of fluid substances under various influences. They incorporate velocity, pressure, density, and viscosity to describe how fluids react to forces. Such as gravity, pressure gradients, and external stresses. Consequently, these equations form the cornerstone of fluid dynamics, enabling scientists and engineers to predict complex flow behaviors in environments ranging from atmospheric weather systems to engineering applications like aircraft design and pipeline flow.

Navier-Stokes Equations Formula

The Navier-Stokes equations are expressed in their simplest form as:

𝜌(∂𝑢/∂𝑡+𝑢⋅∇𝑢)=−∇𝑝+𝜇∇²𝑢+𝑓

• 𝜌 represents the fluid density,
• 𝑢 is the velocity field vector,
• t is time,
• 𝑝 stands for the fluid pressure,
• 𝜇 is the dynamic viscosity,
• ∇ denotes the gradient operator,
• ∇² is the Laplacian operator,
• 𝑓 represents external forces acting on the fluid.

This formula captures the balance of forces acting on fluid elements and is essential for modeling fluid flow dynamics in various physical contexts.

Navier-Stokes Equations Derivation

Deriving the Navier-Stokes equations in a conceptual and non-mathematical way involves integrating fundamental physics principles that govern fluid motion. Here’s a simplified overview of the process:

Step 1: Begin with Newton’s Second Law

The derivation starts with Newton’s second law of motion, which states that the force acting on an object is equal to the mass of the object multiplied by its acceleration. In the context of fluids, this principle is applied not to a single particle, but to a small volume of fluid, known as a fluid element.

Step 2: Consider Fluid Properties

Fluid properties such as density and viscosity are essential. Density relates to the mass per unit volume of the fluid, and viscosity measures the fluid’s resistance to gradual deformation by shear stress or tensile stress.

Step 3: Account for Fluid Forces

The forces acting on a fluid element include:

• Pressure forces, which arise due to changes in pressure within the fluid.
• Viscous forces, which are due to the fluid’s viscosity acting against the flow.
• External forces, such as gravity, that influence the movement of the fluid.

Step 4: Apply Conservation Principles

• Conservation of mass (Continuity equation): This principle states that the mass of the fluid remains constant as it moves, leading to the continuity equation, which expresses the idea that the mass cannot accumulate or deplete in any part of the fluid flow.
• Conservation of momentum: For fluids, the conservation of momentum is expressed by accounting for the sum of the forces (pressure, viscous, and external) and equating this to the rate of change of momentum in the fluid flow.

Step 5: Combine into Equations

Combining these concepts, the Navier-Stokes equations are formed to describe the momentum conservation in fluid dynamics. They mathematically articulate how the velocity of the fluid changes in response to pressure, viscous, and external forces, under the constraint of mass conservation.

Uses of Navier-Stokes Equations

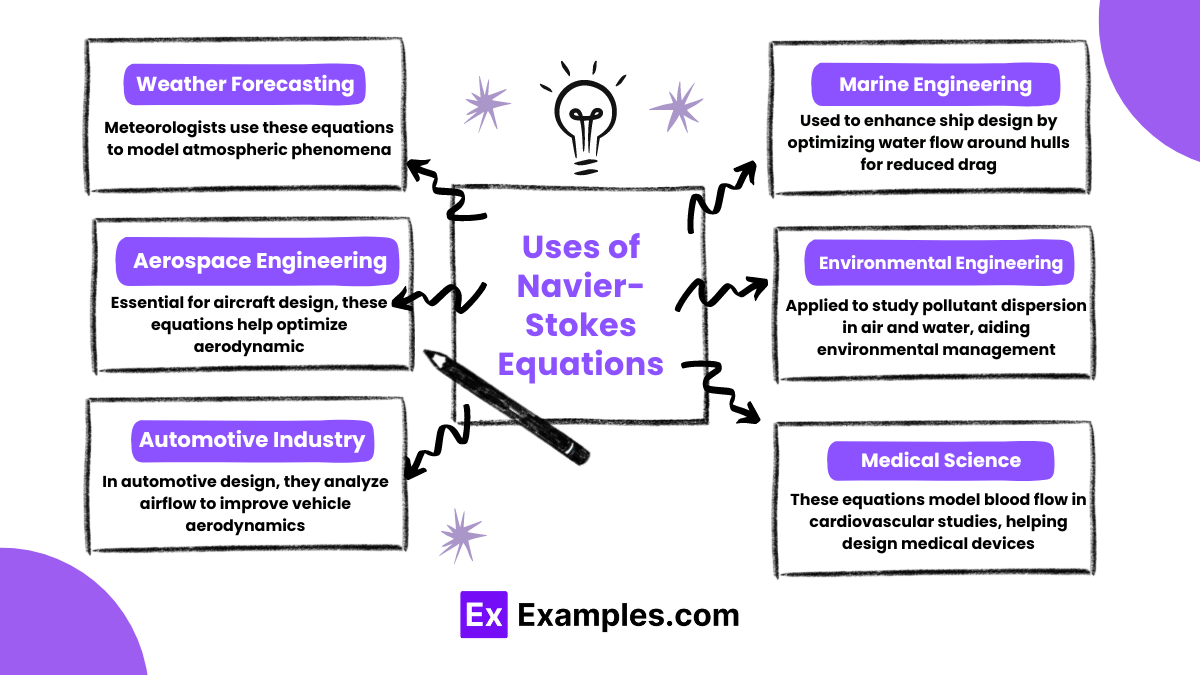
The Navier-Stokes Equations are crucial for understanding fluid dynamics across various fields:

• Weather Forecasting: Meteorologists use these equations to model atmospheric phenomena and forecast weather.
• Aerospace Engineering: Essential for aircraft design, these equations help optimize aerodynamic performance and fuel efficiency.
• Automotive Industry: In automotive design, they analyze airflow to improve vehicle aerodynamics and fuel efficiency.
• Marine Engineering: Used to enhance ship design by optimizing water flow around hulls for reduced drag and increased stability.
• Environmental Engineering: Applied to study pollutant dispersion in air and water, aiding environmental management and mitigation.
• Medical Science: These equations model blood flow in cardiovascular studies, helping design medical devices and treatments.

Examples for Navier-Stokes Equations

The Navier-Stokes Equations are fundamental in various practical applications across multiple fields, showcasing their versatility and critical importance:

• Weather Prediction: Initially, meteorologists utilize the Navier-Stokes equations to simulate atmospheric dynamics. This application enables the accurate modeling of complex weather patterns, including storm systems and temperature fluctuations, essential for daily weather forecasting and long-term climate studies.
• Aerospace Design: Furthermore, aerospace engineers apply these equations to understand airflow over aircraft surfaces. This analysis is crucial for optimizing the design of wings and fuselages to enhance aerodynamic efficiency and safety in flight.
• Automotive Engineering: Similarly, in the automotive industry, the Navier-Stokes equations help engineers study air resistance and heat transfer around vehicles. This knowledge leads to the creation of cars with improved fuel efficiency and reduced emissions.
• Marine Dynamics: Moreover, naval architects use these equations to analyze water flow around ship hulls. Such studies ensure that ships are designed for optimal speed, fuel efficiency, and stability in water.
• Biomedical Applications: Additionally, in the field of biomedical engineering, the equations model blood flow in the human cardiovascular system. This application assists in developing treatments for heart disease and designing devices like stents and heart pumps.
• Environmental Science: In environmental engineering, these equations predict the spread of pollutants in water bodies and the atmosphere, aiding in the development of effective pollution control strategies.
• Industrial Processes: Lastly, they are crucial in optimizing processes that involve fluid flows, such as in chemical reactors, food processing, and the operation of HVAC systems in buildings.

FAQ’S

How many equations is Navier-Stokes?

The Navier-Stokes equations typically consist of three momentum equations (one for each spatial dimension) and one continuity equation, making four in total.

Has the Navier-Stokes equation been solved?

The full solutions for the Navier-Stokes equations in three dimensions under all conditions have not been solved yet; it remains one of the seven Millennium Prize Problems.

Is Navier-Stokes equation hard?

Yes, the Navier-Stokes equation is considered extremely challenging due to its complexity and the nonlinearity in three-dimensional space, posing significant mathematical and computational difficulties.